T - Chemie Unibas

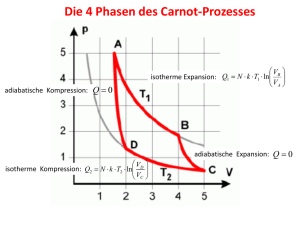
Der Zweite Hauptsatz der TD- Lernziele
o Einleitung
o Entropie (Definition, Entropie
Clausius‘sche Ungleichung)
als
Zustandsfunktion,
die
o Der Zweite Hauptzatz der TD
o Die Entropieänderungen bei speziellen Prozessen
o Der Dritte Hauptsatz der TD
o Die Freie Energie und die Freie Enthalpie
o Freie Standardreaktionsenthalpien
o Die Verbindung von Erstem und Zweitem Hauptsatz (Die
Fundamentalgleichung)
o Die Eigenschaften der Freien Energie, und der Freien Enthalpie
P. Atkins, J. de Paula, “Physikalische Chemie”, Wiley-VCH Verlag GmbH&
Co, 2013, 3.1-3.3.
G. Wedler, H-J. Freund, „Lehrbuch der Physikalischen Chemie“, Wiley-VCH
Verlag GmbH& Co, 2013, 1.1.18-1.1.22.
Einleitung
Unser Ziel: wann und warum
Umwandlungen freiwillig ablaufen?
physikalische
und
chemische
Vorgänge:
- die freiwillig – von selbst- ablaufen
- die nicht freiwillig ablaufen.
z. B.
Tw
Tk
Tw > Tk
Tg
Freiwillige Prozesse
Freiwillige Prozesse = Prozesse die mit einer naturgegebenen Neigung, von
selbst abzulaufen.
Wichtig: in der Praxis können diese Prozesse stattfinden oder auch nicht.
?
Der Zweite Hauptsatz der TD (Kelvin Formulierung) : Ein Prozess, bei
dem lediglich Wärme aus einem Reservoir entnommen und vollständig in
Arbeit umgewandelt wird, ist unmöglich.
Die Richtung freiwilliger Prozesse
Freiwillige Prozesse sind immer mit einer Disipation von Energie
verbunden.
z. B. Die Richtung freiwilliger Zustandsänderung für einen Ball der den
Boden entlang springt.
- bei jedem Aufprall
Ekin
Ethermisch
Ungeordnete Bewegung von Molekülen
Die Richtung freiwilliger Prozesse
Die ungeordnete Energieverteilung ist nicht von selbst in eine ordnente
Bewegung verwandelt.
z. B.
- Ein Gas zieht sich nicht freiwillig auf ein kleineres Volumen zusammen.
- Ein kalter Gegenstand wird nicht spontan wärmer als die Ungebung.
- Ein Ball liegt auf einem
wärmeren Untergrund (a).
?
Das Streben zur grosserer Unordnung ist die treibende Kraft jeglicher
Veränderung (zur Verteilung von Energie und Materie).
Der Carnot’sche Kreisprozess
Wir benötigen ein ideales Gas.
1. Reversible, isotherme Expansion
V1, T1
V2, T1
V2 > V1
dU = 0 dT = 0
QT1 = Wärmemenge wird aus dem
Wärmebad entnommen.
V2
3. Reversible, isotherme Kompression
V3, T2
V4, T2
V3 > V4
dU = 0 dT = 0
QT1 = Wärmemenge wird an die kalte
Umgebung abgegeben.
V3
V4
V1
2. Reversible, adiabatische Expansion
V2, T1
V3, T2
V3 > V2 und T2 < T1
dQ = 0
γ −1
γ −1
T 1V 2
= T 2V 3
4. Reversible, adiabatische Kompression
V4, T2
V1, T1
V4 > V1 und T2 < T1
dQ = 0
γ −1
γ −1
T 1V 1
V4
V3
V2
= T 2V 4
V1
Der Carnot’sche Kreisprozess
Geleisteten Volumenarbeiten ergeben sich als Fläche
zwischen den Isothermen und Adiabaten:
V2
W 1 = − nRT 1 ln
V1
W 2 = nC V , m (T 2 − T1 )
V3
V4
W 4 = nC V , m (T1 − T 2 )
W 3 = nRT 2 ln
Die gesamte Arbeit :
W = nR ln
V2
(T 2 − T1 ) = nR ln V 2 ∆ T
V1
V1
W <0
V1 < V2 und T2 < T1
Wärmekraftmaschine
Der Carnot’sche Kreisprozess
Die Aenderung der Inneren Energie bei dem gesamten Kreisprozess:
∆ U = nc V , m (T 2 − T1 ) + nc V , m (T1 − T 2 ) = 0
Bei den Isothermen ∆U = 0
Bei den adiabatischen Schritten eintretenden Aenderungen kompensieren.
Q = nRT 1 ln
V2 V3
=
V1 V4
V
V2
− nRT 2 ln 3
V1
V4
Q = nR ln
V2
(T1 − T 2 ) > 0
V1
Das Arbeitgas entnimmt einem Thermostaten hoher Temperatur eine
Wärmemenge und leisted eine Arbeit (gibt auch eine restliche
Wärmemenge an einen Thermostaten tieferer Temperatur).
Wärmekraftmaschine / Wärmepumpe
Kann man einen höheren Wirkungsgrad mit einer anderen Maschine
erreichen?
Maschine dann als Wärmepumpe benützen, um einen CarnotProzess anzutreiben!
T1
Annahme:
Der Wirkungsgrad von A ist höher als der,
der Maschine B !
W
QT1
QT1
w‘‘
Q
T
Q
QT2
2
QT2 T
2
T2
Da der Wirkungsgrad der Maschine A höher
ist, wird von A mehr Arbeit produziert als von
der Maschine B aufgenommen wird, um die
Wärmemenge QT1 wieder dem warmen
Reservoir zuzuführen!‘
X
Wärmekraftmaschine
Die Wärmekraftmaschine :
- das Arbeitsgas entnimmt dem wärmeren Reservoir die Wärmemenge QT1,
- leistet die Arbeit W
- führt dem kleineren T Reservoir die Wärmemenge
T1
QT2 = QT1 – W zu
QT1
Das Carnotische Kreisprozess:
- Aufnahme einer QT1 von einem Thermostaten (T1)
- Abgabe einer QT2 an einem Thermostaten (T2)
Arbeit ist gewonnen !
QT2
T2
Die Wärmekraftmaschine
Wärmepumpe
Der Prozess läuft in entgegengesetzter Richtung:
Die Wärmepumpe:
- das Arbeitsgas entnimmt dem kälteren Reservoir die Wärme QT2
- pumpt sie mit kleinerem Arbeitsaufwand w‘ (als gesamte Wärmemenge QT1)
in das wärmere Reservoir
Eine gegenüber der ursprünglichen Wärmemenge
QT1 - um den
Arbeitsbetrag w‘ verminderte Wärmemenge - fliesst zurück ins wärmere
Reservoir!
Wirkungsgrad der Wärmekraftmaschine
Wirkungsgrad η der Wärmekraftmaschine = geleistete Arbeit geteilt
durch die aufgenommene Wärme
η=
w
QT1
V2
−nR(T1 − T2 ) ln
w
V1 T1 − T2
T
η=
=
=
= 1− 2
V
T1
T1
QT1
nRT1 ln 2
V1
Da 0 < T2 < T1
0<η<1
Carnot’scher Kreisprozess
Bei diesem Kreisprozess würde Wärme in Arbeit umgewandelt, ohne
dass
irgendwelche
Veränderungen
eintreten
Widerspruch
zur
Erfahrung.
2. Hauptsatz der TD: Es gibt keine Wärmekraftmaschine mit
höherem Wirkungsgrad, als den Carnot-Prozess!
An dem reversibel durchgeführten Carnot‘schen
Kreisprozess lässt sich eine interessante
Funktion ableiten!
Reduzierte Wärme
Betrachte: Mit der Umgebung ausgetauschte Wärmemenge beim Carnot‘schen
Prozess (Verhältnis, der mit der Umgebung ausgetauschten Wärmemenge)
V 
nRT1 ln  2 
Q
 V1  T1
− T1 =
=


QT2
T2
V
nRT2 ln  3 
 V4 
d.h.
 V2 
= nRln  
T1
 V1 
QT1
 V4 
 V2 
und
= nRln   = −nRln  
T2
 V3 
 V1 
QT2
Q QT1 QT2
=
+
=0
∑
T1 T2
rev T
Die Summe der reduzierten Wärmen
Q/T ist null beim Carnot‘schen-Prozess!
Ist die reduzierte Wärme eine Zustandsfunktion?
Wenn Q/T eine Zustandsfunktion ist, muss ihre Aenderung unabhängig vom
Weg sein!
z. B. Carnot’scher Kreissprozess
1+2
A Zustand
p1, V1, T1
C Zustand
p2, V3, T2
p2, V2, T2
3+4
Q
V2
=
nRln
∑T
V1
1+2
Q
V
V
∑ T = −nRln V3 = −nRln V2
4
1
3+4
Die reduzierte Wärme ist eine
Zustandsfunktion
Beliebige Kreissprozesse
Man kann jeden beliebigen reversiblen Kreisprozess näherungsweise in eine
Anzahl von Carnot-Prozessen zerlegen.
Zweckmässiger Weisse führt man statt summieren eine Integration durch
∫
dQrev
=0
T
oder
∫
dQirr
>0
T
Q/T ist ein Mass für die Irreversibilität eines Vorgangs!
Die Entropie
Die Entropie (S) ist ein Mass für die Disipation der Energie bei einem
bestimmten Prozess.
Entropie ist eine Grösse, die die Richtung freiwillig (spontan) ablaufender
Vorgänge vorhersagt!
Der Begriff Entropie = tropé (Wendung) und entrépein (umwenden, eine
Richtung geben)
Die
Entropieformulierung
beschreibt
welche
der
erlaubten
Zustandsänderung freiwillig ablaufen
Bei einer freiwilligen Zustandsänderung eines abgeschlossenen Systems:
∆Sgesamt > 0
TD Definition der Entropie
Die Uebertragung von Wärme: thermische Bewegung der Teilchen
der Umgebung.
Die Uebertragung von Energie in Form von Arbeit: geordnete
Bewegung der Teilchen der Umgebung.
dQrev
= dS
T
Thermodynamische Definition der Entropie:
Für endliche Zustandsänderung:
E
dQrev
T
A
∆S = ∫
TD Definition der Entropie
z. B.: freie Expansion eines Gases
Gesamtenergie (Innere Energie) bleibt konstant, aber die Verteilung der
Gasmoleküle ändert sich!
‚Qualität‘ der Energie nimmt ab!
‚Spontane Vorgänge sind eine Folge des Strebens der Welt nach grösserer
Unordnung‘
Einheit: [S ] = JK-1
S ist eine extensive Eigenschaft.
Entropie
z. B. Beim schmelzen von Eis: die geordnete Eiskristallstruktur wird in eine
regellose Bewegung einzelner Wassermoleküle überführt.
Energie und Entropie vom Getränk werden auf die Wassermoleküle des
Eiswürfels übertragen.
Eigenschaften der S:
Die Entropie bleibt nur dann unverändert, wenn die Prozesse reversibel
verlaufen (für ein Kreisprozess).
Reale Zustandsänderungen sind immer mit Energieverlusten (z. B. durch
Reibung) verbunden, wodurch sich die Entropie erhöht.
Eine Verringerung der Gesamtentropie in einem geschlossenen System ist
nicht möglich.
Mikroskopische Interpretation der Entropie
Die Energie eines Atoms oder Moleküls kann nur
bestimmte Werte annehmen
die Energienivaus
T > 0 → die Molekule einer Probe sind auf alle
verfügbaren Energienivaus verteilt
Es ist nicht möglich, den Energiezustand eines
einzelnen Moleküls zu verfolgen
Aussage über die mittlere Anzahl der Moleküle in
jedem Zustand
Mikroskopische Interpretation der Entropie
Boltzman Verteilung
die mittlere Anzahl der Molekule in jedem Zustand
Population der Moleküle – für jeden Zustand
T=0
Nur der Zustand niedrigster Energie ist besetzt
T ↗
Mehr Zustande sind für die Moleküle erreichbar
Ni = N exp (-Ei /kBT) / ∑ exp (-Ei /kBT)
Anzahl der Moleküle einer Probe (N Moleküle) → die
Energiezustand Ei besetzen (bei T – System in
thermischem Gleichgewicht)
kB = 1,3807·10-23 J/K
(die Boltzmann Konstante)
Mikroskopische Interpretation der Entropie
Boltzmann Formel
Die Verbindung zwischen der Verteilung
der Moleküle auf die Energienivaus und
die Entropie
S = k ln (W)
W – die Anzahl der Mikrozustände (die
unterschiedlichen
Möglichkeiten,
die
Moleküle bei gegebener Gesamtenergie
eines Systems auf die zur Verfügung
stehenden Energienivaus sich verteilen).
Mikroskopische Interpretation der Entropie
Die Entropie eines Makrozustands →
statistisches
Gewicht W (die Anzahl seiner Mikrozustände).
n Molekule auf zwei Raumhälften: n1 – einer Hälfte, n2 –
andere Hälfte. n ist ein ganzes Mol (6,0220·1023 Mol-1 )
und
Bei gleichmässiger Aufteilung:
Stirling Formel:
Damit wird
die Entropie nach der Expansion
Weitere PCi Vorlesung
?
Aktuelle Endekungen
Der TD Zeitpfeil beruht auf dem Zweiten Hauptsatz der TD: Die Zukunft ist
die Zeitrichtung, in der die Entropie zunimmt.
Ein interessanter Punkt ist, dass dieser Zeitpfeil im thermodynamischen
Gleichgewicht nicht existiert: Für einen Gleichgewichtszustand gibt es keine
thermodynamisch
definierte
Vergangenheit
und
Zukunft;
der
Gleichgewichtszustand ist sozusagen zeitlos.
Die Zukunft ist die Richtung des
grösseren Universums (die
Entropie nimmt zu!).
17.03.2014: Astrophysiker haben in der Kosmischen Hintergrundstrahlung
erstmals Hinweise auf Gravitationswellen endeckt (Kosmische Inflation)
Entropie: Zustandsfunktion
Entropie: Zustandsfunktion, die anzeigt, ob ein Zustand von einem anderen
aus, spontan erreichbar ist.
Entropie ist ein Bindeglied zwischen makroskopischer und mikroskopischer
Welt!
2. Hauptsatz:
Ein Prozess, bei dem lediglich Wärme aus einem
Reservoir entnommen und vollständig in Arbeit umgewandelt wird, ist
unmöglich!
2. Hauptsatz: Bei einer freiwilligen Zustandsänderung nimmt die Entropie
eines abgeschlossenen Systems zu!
Die Clausius’sche Ungleichung
Reversible Prozessbedingungen → mehr Energie (in Form
von Arbeit) als bei irreversiblen Prozessen
- dwrev ≥ - dw → dw – dwrev ≥ 0
Die Aenderung der U zwischen A und E:
d U = dQ + dw = dQrev + dwrev
dQrev – dQ = dw – dwrev ≥ 0
dQrev/T ≥ dQ/T
d S = dQrev/T
dQ = 0 (abgeschlossenes System) ←
dS ≥ dQ/T
dS ≥ 0 Die S eines abgeschlossenen Systems
freiwilligen
Zustandsänderung
kann nicht abnehmen
(der zweite Hauptsatz der TD).
Entropieänderung bei speziellen Prozessen
Freiwillige Abkühlung
1. Einem warmen Reservoir wird eine
Wärmemenge entzogen → sinkt seine
Entropie.
(Führt man dieselbe Wärmemenge zu)
2. Einem kalten Reservoir → steigt dessen
Entropie um einen grösseren Wert.
Daher nimmt die Entropie während des
Prozesses insgesamt zu, und dieser läuft
freiwillig ab.
dS = dQ/Tw
dQ
dS = dQ/Tk
Entropieänderung bei speziellen Prozessen
Freiwillige Abkühlung
dS
≥ dQw/Tw + dQk/Tk
dS = dQ/Tw
dQw = - dQk
dS ≥ -dQk/Tw + dQk/Tk = dQk (1/Tk – 1/Tw)
dQ
dQk > 0
dS ≥ 0 → die Abkühlung ist immer freiwillig
dS = dQ/Tk
Nimmt S während des Prozesses insgesamt zu
Der Prozess läuft freiwillig ab.
Entropieänderung bei speziellen Prozessen
Isotherme Expansion
Die logarithmische Zunahme der Entropie
eines idealen Gases bei der isothermen
Expansion.
∆U = Qrev + wrev = 0 ⇒ Qrev = - wrev
dS = dQrev /T
E
1
Q
∆S = ∫ dQrev = rev
T A
T
Isotherme Expansion → wrev = - nRT ln(VE/VA)
∆S = nR ln
VE
VA
S ist eine Zustandsfunktion → die
Gleichung kann für reversible/irreversible
Zustandsänderung angewendet werden.
Entropieänderung bei speziellen Prozessen
Phasenübergänge
Sieden / Erstarren:
Ttrans: Eine T wo sich zwei Phasen (bei 1 bar) miteinander im
Gleichgewicht befinden
Wärmeaustausch zwischen beiden Phasen → reversibel
p = konstant
Q = ∆trans H
∆ S = ∆transH / Ttrans
Exotherme Phasenübergänge: ∆trans H < 0
∆S<0
( bei diesen Phasenübergängen können Energie und Materie lokalisiert
werden)
Endotherme Phasenübergänge: ∆trans H > 0
∆S>0
(Energie und Materie werden verteilt)
Entropieänderung bei speziellen Prozessen
Temperaturänderungen
E
dQrev
T
A
∆S = ∫
S kann berechnet werden
(bei einer beliebigen T)
E
S(TE) = S(TA) +
z.B.
p konstant
dQrev
∫A T
dQrev = cpdT
E
S(TE) = S(TA) +
∫
c p dT
A
T
(keine Expansionarbeit) + cp konstant
S(TE) = S(TA) + cp ln(TE/TA)
Entropieänderung bei speziellen Prozessen
Temperaturänderungen
Analog (Austauch von cp gegen cv)
gilt die Gleichung für konstantes Volumen
Die Entropie eines Systems der Temperatur T → kann auf seine Entropie
bei T = 0 zurückgeführt werden
cp bei verschiedenen T gemessen und das Integral auswertet
Man muss die jeweilige Phasenübergängsentropie ∆trans H/T
addieren.
Entropieänderung bei speziellen Prozessen
Temperaturänderungen
Beispiel: Eine Substanz schmilzt bei TSm und siedet bei
Ts
Die Entropie entspricht der Summe aus der Fläche
unter der oberen Kurve (bei cp/T = f(T)) und den
Entropien aller durchlaufenen Phasenumwandlungen
S (T ) = S (0 ) +
TSm
∫
0
TS
c p (l )
c p (g )
c p (s )
∆ Sm H
∆ H
dT +
+ ∫
dT + V + ∫
dT
T
TSm
T
T
T
S
TSm
TS
T
Phasenübergänge müssen berücksichtigt werden.