KLASSENARBEIT MATHEMATIK G9B

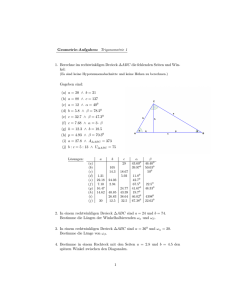
KLASSENARBEIT MATHEMATIK G9B
22.11.2012
1 2 3 4 5 6 7 8
Aufgabe
Punkte (max) 6 3 4 3 3 3 6 2
Punkte
(1) Berechne
(−3)4 =
−42 =
2m 2n =
a2+m : am−1 =
(xa+1 )2 =
161/4 =
(2) Werner kann bei ausgestrecktem Arm (Armlänge 80 cm) mit
seinem 2 cm breiten Daumen die 120 m lange Eisenbahnbrücke
gerade verdecken. Wie weit ist er von der Brücke entfernt?
(3) Bestimme die Breite des Flusses für a = 75 m, b = 50 m und
c = 47 m:
(4) Bestimme x im Diagramm rechts oben.
(5) Welchen Höhenunterschied überwindet man auf einem Wanderweg mit einer Steigung von 18 %, wenn man 100 m geht?
Bestimme auch den Neigungswinkel des Wegs.
(6) Von einem rechtwinkligen Dreieck kennt man die Kathete a = 8
cm und den Winkel α = 30◦ . Bestimme alle Winkel und Seitenlängen.
2
22.11.2012
(7) In der Nische einer Dachschräge soll in 1 m Höhe ein Boden aus
Glas angebracht werden.
An welcher Stelle des schrägen Bretts (von unten gerechnet)
muss ein Träger für den Boden angebracht werden?
Wie lang muss der Glasboden sein?
Wie groß ist der Neigungswinkel des schrägen Bretts?
(8) Bestimme x und y in folgendem Dreieck:
KLASSENARBEIT MATHEMATIK G9B
3
Lösungen
(1) Berechne
(−3)4 = 81
−42 = −16
a2+m : am−1 = a3
(xa+1 )2 = x2a+2
2m 2n = 2m+n
161/4 = 2
(2) Werner kann bei ausgestrecktem Arm (Armlänge 80 cm) mit
seinem 2 cm breiten Daumen die 120 m lange Eisenbahnbrücke
gerade verdecken. Wie weit ist er von der Brücke entfernt?
Strahlensatz:
4,8 km.
80
2
=
x
120
gibt x = 4800. Die Entfernung beträgt
(3) Bestimme die Breite des Flusses für a = 75 m, b = 50 m und
c = 47 m.
Strahlensatz:
x
a
= cb , also x = 70,5 m.
(4) Bestimme x im Diagramm rechts oben.
Strahlensatz
x
4
=
x+2
6
liefert 6x = 4x + 8, also x = 4.
(5) Welchen Höhenunterschied überwindet man auf einem Wanderweg mit einer Steigung von 18 %, wenn man 100 m geht? Bestimme auch den Neigungswinkel des Wegs.
Für den Neigungswinkel α gilt tan α = m = 0, 18, also α = 10,◦ .
Daraus folgt dann sin α =
h
,
100
also h = 17, 7 m.
(6) Von einem rechtwinkligen Dreieck kennt man die Kathete a = 8
cm und den Winkel α = 30◦ . Bestimme alle Winkel und Seitenlängen.
Es ist β = 90◦ − 30◦ = 60◦ . Weiter ist sin 30◦ = 8c , also c = 16,
√
√
sowie b = c2 − a2 = 192.
(7) In der Nische einer Dachschräge soll in 1 m Höhe ein Boden
aus Glas angebracht werden.
An welcher Stelle des schrägen Bretts (von unten gerechnet)
muss ein Träger für den Boden angebracht werden?
Wie lang muss der Glasboden sein?
4
22.11.2012
Wie groß ist der Neigungswinkel des schrägen Bretts?
Der Neigungswinkel α genügt tan α =
2,5
,
2
also ist α = 51, 3◦ .
Für die Länge ` des Glasbodens erhält man
1, 2. Der Glasboden ist 1,2 m lang.
`
1,5
=
2
,
2,5
h
1
=
3,2−h
,
1,5
Für die Höhe h auf dem schrägen Brett folgt
= 1,28 m.
also ` =
also h
(8) Bestimme x und y in folgendem Dreieck.
Aus x4 =
y = 12.
x
16
folgt z 2 = 64, also x = 8. Danach
y
12
=
x
x
= 1, also