Formelsammlung Physik I Schrewe

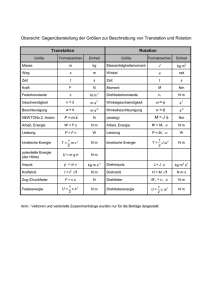
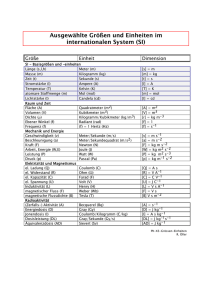
Hochschule Hannover
Fakultät II Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I
Formelsammlung
----------------------------------------------------------------------------------------------------------------KINEMATIK
Translation
Rotation
Verschiebung:
Geschwindigkeit:
Beschleunigung:

s

 ds
v
dt


 dv d 2 s

a
dt dt 2
Gleichförmige Geschwindigkeit
 


s  v t
v  const.
a0
Drehwinkel:
Winkelgeschwindigkeit:
Winkelbeschleunigung:



d

dt


 d d 2
 2

dt
dt

Gleichförmige Winkelgeschwindigkeit
 


   t
  const.
 0
Gleichförmige Beschleunigung
Gleichförmige Winkelbeschleunigung
 

 1 2

 

1
v  a t
a  const.
s  a t
   t2    t
  const.
2
2
-----------------------------------------------------------------------------------------------------------------------v  r 
a  r 
Bahngröße = Radius * Winkelgröße:
s  r 
-----------------------------------------------------------------------------------------------------------------------dN
1
n
Drehzahl:
Umdrehungszeit:
T
dt
n
2  r
2
Bahngeschwindigkeit:
v
 2  r  n Winkelgeschwindigkeit:

 2  n
T
Τ
v2
Zentripetalbeschleunigung: a r 
 v    2  r
r
-----------------------------------------------------------------------------------------------------------------------

Zerlegung einer beliebigen Beschleunigung in Tangential-( T ) - und Normalbeschleunigung ( N )


dv
dv

aT  T
aN  N
a  aT  T  a N  N
dt
dt
v
v
v
y
aT  x  a x   a y  z  a z
a N  a 2  aT2
v
v
v
-----------------------------------------------------------------------------------------------------------------------DYNAMIK
Translation
Rotation
Masse:
m
Trägheitsmoment:
J   mi  ri 2   r 2  dm
i



  
 dp

d
L
Kraft:
F  ma 
Drehmoment:
M  r  F  J  
dt
dt


  

p  mv
Impuls:
L  r  p  J 
Drehimpuls:
 
 
dW  F  ds
Arbeit:
dW  M  d
Arbeit:
 
 
W   F  ds
W

M
 d

 ds  
dW
 d
 
dW
P
F
 F v
Leistung:
Leistung:
P


M


M

dt
dt
dt
dt

1

1
Bewegungsenergie: Etrans   m  v 2
Bewegungsenergie: E rot   J   2
2
2
Prof. Dr. U. J. Schrewe, Physik I: Formelsammlung - 2012 Seite 1
Hochschule Hannover
Fakultät II Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I
Formelsammlung
---------------------------------------------------------------------------------------------------------Federkonstante:
Federkraft:
Verformungsarbeit:
Haftreibungszahl:
Haftreibungskraft:
Gleitreibungskraft:
Rollreibungskraft:
Feder- Drehfederkräfte, elastische Verformungsarbeit
D
Winkelrichtgröße:


Fel   D  s
Drehfedermoment:
1
Wel  D  s 2
Verformungsarbeit:
2
H
Reibungskräfte, Reibungsarbeit
Gleitreibungszahl:
G
FH ,max   H  FN
FG   G  FN
FR   R  FN
D*


M el   D*  
1
Wel  D *   2
2
Rollreibungszahl:
R
Gleitreibungsarbeit: WG  FG  s   G  FN  s
Rollreibungsarbeit: WR  FR  s   R  FN  s
Gravitationskräfte, potentielle Energie im Gravitationsfeld
Gravitationskonstante:
G = 6,67 10-11 N m2 kg-2

M m
M m
Gravitationskraft:
potentielle Energie: E (r )  G 
Fg  G  2
r
r
Erdradius:
RE
Erdbeschleunigung: g = 9,81 m s-2
Masse der Erde:
ME
 M 
Gewichtskraft:
Fg  m   G  2E   m  g potentielle Energie: E (h)  m  g  h
RE 

Fehlen äußere Kräfte:

F
 i 0
i
gilt Impulserhaltung:

p
i
Erhaltungssätze
Fehlen Drehmomente:
 konst.
gilt Drehimpulserhaltung:
i

M
i i  0

L
 i  konst.
i
In einem System mit konservativen Kräften bleibt die mechanische Energie erhalten:
kin
kin
E ges  E pot  Etrans
 E rot
In einem System mit nicht-konservativen Kräften (z.B. Reibungskräften) geht ein Teil Q der
mechanischen Gesamtenergie verloren (z. B. in Wärme oder Verformungsenergie):
kin
kin
E ges  E pot  Etrans
 E rot
Q
Wirkungsgrad:

E ges  Q
E ges

Wnutz
E ges
Anwendungen
Wird ein Körper der Masse M um eine Achse gedreht, deren Abstand zum Schwerpunkt h ist, gilt:
J ges  M  h 2  J S ,
wobei JS das Trägheitsmoment bezüglich des Schwerpunktes bezeichnet (Steinerscher Satz).
Trägheitsmoment geometrischer Körper:
J  k mr2
Hohlzylinder (Ring): k = 1, Vollzylinder (Scheibe): k = 1/2, Vollkugel: k = 2/5, Hohlkugel: k = 2/3
dünner Stab mit Drehpunkt Mitte: k = 1/12, dünner Stab mit Drehpunkt Ende: k = 1/3,
Trägheitsmoment flacher Körper (Ausdehnung in x- und y-Richtung): J z  J x  J y
Prof. Dr. U. J. Schrewe, Physik I: Formelsammlung - 2012 Seite 2
Hochschule Hannover
Fakultät II Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I
Formelsammlung
---------------------------------------------------------------------------------------------------------Trägheitskräfte im beschleunigten Bezugssystem:


FTr  ma

v2
FZf  m
r

 
FCor  2  m    vr
Trägheitskraft:
Zentrifugalkraft:
Corioliskraft:
Geschwindigkeit zum Zeitpunkt t = 0:
Geschwindigkeit zum Zeitpunkt t:
Ausströmungsgeschwindigkeit:
Raketengleichung:

v0
Masse zum Zeitpunkt t = 0: m0

v (t ) Masse zum Zeitpunkt t:
m(t )

u aus
m



v (t )  u aus  ln 0  v0
m(t )
Zentraler elastischer Stoß:


Vor dem Stoß: Geschwindigkeit der Masse m1 ist v1 , Geschwindigkeit der Masse m2 ist v 2 .


Nach dem Stoß: Geschwindigkeit der Masse m1 ist u1 , Geschwindigkeit der Masse m2 ist u 2 .
2m 2
2m1

 m  m2 

 m  m1 
u1 
u2 
 v1  2
 v2
 v2  1
 v1
m1  m2
m1  m2
m1  m2
m1  m2
Zentraler vollkommen unelastischer Stoß:


Vor dem Stoß: Geschwindigkeit der Masse m1 ist v1 , Geschwindigkeit der Masse m2 ist v 2 .


Nach dem Stoß: Geschwindigkeit der Masse m1 ist u , Geschwindigkeit der Masse m2 ist u .
m2
m1


 v1 
 v2
m1  m2
m1  m2
Verformungsarbeit beim vollkommen unelastischen Stoß:

u
WQ



1
1
1
m 1  v 12  m 2  v 22  m 1  m 2   u 2
2
2
2


m2  p1  p 2
m1 
1
2
  E kin
 
WQ  E kin
 1 
 1 
 m1  m2 
 m1  m2  m1  m2
W Q 
Gleiten:
Rotieren:
Rollen:
Gleiten, Rotieren, Rollen
 
 

v (r )  v (r )  v S
Geschwindigkeit des Schwerpunktes:
 
 
v (  r )  v ( r )
Geschwindigkeit des Schwerpunktes:

v Kontakt  0
Geschwindigkeit des Schwerpunktes:
Rollen:
Verschiebung des Schwerpunktes:
Rollen:
Beschleunigung des Schwerpunktes:

vS

vS

vS

sS

aS
0
 
 R 
 
 R 
 
 R 
Prof. Dr. U. J. Schrewe, Physik I: Formelsammlung - 2012 Seite 3
Hochschule Hannover
Fakultät II Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I
Formelsammlung
---------------------------------------------------------------------------------------------------------------------------Formelzeichen und Einheiten

a
Beschleunigung
1 m s-2
D
Federkonstante
1 N m-1
D*
Winkelrichtgröße
1 kg m2 s-2
E

F
Energie
1 J = 1 N m = 1 kg m2 s-2
Kraft
1 N = 1 kg m s-2
g
Erdbeschleunigung
9,81 m s-2
G
Gravitationskonstante
6,67 10-11 N m2 kg-2
J

L
Trägheitsmoment
1 kg m2
Drehimpuls
1 kg m2 s-1
m

M
Masse
1 kg
Drehmoment
1 kg m2 s-2
n
Drehzahl
1 s-1
N

p
Zahl der Umdrehungen
Impuls
1 kg m s-1
P
Leistung
1 J s-1 = 1 N m s-1 = 1 kg m2 s-3
Q
Wärmeenergie
1 J = 1 N m = 1 kg m2 s-2
r

s
Radius
1m
Verschiebung
1m
t
Zeit
1s
T

v
Umdrehungszeit
1s
Geschwindigkeit
1 m s-1
W
Arbeit
1 J = 1 N m = 1 kg m2 s-2

Winkelbeschleunigung
1 s-2

Wirkungsgrad
H
Haftreibungszahl
G
Gleitreibungszahl
R
Rollreibungszahl





Drehwinkel
Winkelgeschwindigkeit
1 s-1
Prof. Dr. U. J. Schrewe, Physik I: Formelsammlung - 2012 Seite 4