Schaltung mit MOS
Werbung

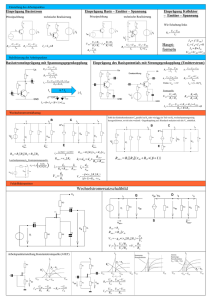
Schaltung mit MOS-Transistor In Bild 8-1 ist eine Verstärkerschaltung mit dem MOS-Transistor T dargestellt. Der Transistor soll im „aktiven Bereich“ mit einem Strom ID = 2 mA betrieben werden. Als TransistorμA Parameter sind bekannt: UGS0 = Ut = 2 V, μ n ⋅ cox = 10 und W = 100. L V2 Weitere Angaben: R1 = 2 MΩ, R2 = 1 MΩ, UB = 24 V. UB I1 R1 R3 T R2 R4 Bild 8-1 Schaltung mit n-Kanal MOS-Transistor 8. Aufgabe 1 Schaltung mit MOS-Transistor a) Bestimmen Sie die den Strom I1. b) Berechnen Sie für den geforderten Betriebsfall die Spannung UGS. c) Bestimmen Sie den Wert des Widerstandes R4, der zur Einstellung der unter b) berechneten Spannung zwischen Gate- und Source- Anschluss erforderlich ist. d) Welche Bedingung muss der Widerstand R3 erfüllen, damit ein Betrieb des Transistors im Abschnürbereich (Sättigungsbereich) sichergestellt ist? 8. Aufgabe 2 Schaltung mit MOS-Transistor-Lösung a) I K1 I1 ID UR1 R1 K2 I2 UR2 R2 R3 G IG U GS D T S R4 UB UR3 UDS UR4 8. Aufgabe 3 Schaltung mit MOS-Transistor-Lösung a) In der Schaltung können folgende Hauptmaschen festgelegt werden: M1: − U B + U R 1 + U R 2 = 0V M2: − U B + U R 3 + U DS + U R 4 = 0V M3: − U R 4 − U GS + U R 2 = 0V Außerdem ergeben sich die Knotengleichungen K1: I = I D + I1 und K2: I1 = I 2 + IG Wegen IG = 0 gilt I1 = I2 . Damit kann M1 umgestellt werden zu: U B = I1 ⋅ R 1 + I1 ⋅ R 2 und I1 = UB R1 + R 2 I1 = 24 V = 8 μA 2 MΩ + 1 MΩ 8. Aufgabe 4 Schaltung mit MOS-Transistor-Lösung b) Bestimmung von UGS für vorgegebenes ID = 2⋅10-3 A ID R1 UB R3 UR3 T UDS R4 UR4 UGS UR2 R2 ID Für die Berechnung von UGS wird aufgrund der Annahme „aktiver Bereich“ in der Aufgabenstellung die Formel ID = W 1 2 ⋅ K n ⋅ ⋅ (U GS − U t ) mit K n = μ n ⋅ c OX benutzt. L 2 8. Aufgabe 5 Schaltung mit MOS-Transistor-Lösung 10μA 1 2 ⋅ U U ( ) GS t V2 2 1 mA 2 2mA = ⋅ ⋅ ( U GS - 2 V ) 2 2 V 2mA = 100 ⋅ U GS = 2 V ± 4 V2 Damit kann UGS die Werte 4V und 0V annehmen. Da für U GS = 0V und U t = 2V , also U GS < U t , der Transistor im Sperrbereich arbeiten würde, kann auch kein Strom ID fließen. Die Lösung U GS = 0V steht damit in Widerspruch zur Aufgabenstellung. Damit verbleibt als Lösung U GS = 4V . 8. Aufgabe 6 Schaltung mit MOS-Transistor-Lösung c) Berechnung von R4 Der Spannungsumlauf am Eingangskreis ergibt: U R2 = U GS + U R4 = U GS + I D ⋅ R 4 (1) Da beim MOSFET für den Gate- Strom IG = 0 angenommen werden kann, ergibt sich UR2 nur aus dem Spannungsteiler mit R1 und R2: R2 U R2 = U B ⋅ (2) R1 + R 2 (2) in (1) eingesetzt und nach R4 aufgelöst ergibt: UB ⋅ R4 = R2 1MΩ − U GS 24V ⋅ − 4V R1 + R 2 2M 1M Ω + Ω = = 2 kΩ ID 2mA 8. Aufgabe 7 Schaltung mit MOS-Transistor-Lösung d) Berechnung von R3 Die Grenze vom Triodenbereich zum Abschnürbereich (Sättigungsbereich) wird von folgender Bedingung aus der Vorlesung bestimmt: U DS ≥ U GS − U t hier: UDS,MIN = 4V – 2V = 2V (UGS aus Teil a) Die Grenze wird also durch eine minimale Drain- Source- Spannung UDS,MIN bestimmt. Ein weiterer Zusammenhang für UDS ergibt sich aus dem Spannungsumlauf im Ausgangskreis: U B = U R3 + U DS + U R4 = U DS + I D ⋅ (R 3 + R 4 ) Man beachte, dass IS = ID gilt. Die Formel nach R3 aufgelöst: R3 = U B − U DS − R4 ID Setzt man UDS,MIN für UDS, ergibt sich der folgende Maximalwert für R3 (wegen des Vorzeichens von UDS!) für R3: U B − U DS,MIN 24V − 2V − R4 = − 2kΩ = 9kΩ R 3,MAX = 2mA ID 8. Aufgabe 8