Protokoll der Physikstunde vom 31

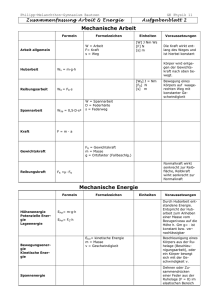
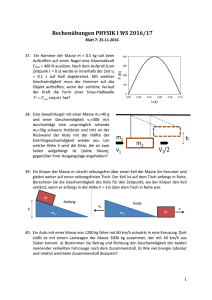
Protokoll der Physikstunde vom 27.03.06
Unterrichtseinheit: Energie und Energieerhaltung
Stundenthema:
Formen der Arbeit
Protokollantin:
Sabrina Frank
Tagesordnungspunkte:
1. Beispiel für die zunehmende Kraft
2. Hubarbeit
a) Beschreibung
b) vertikales Heben
c) Schiefe Ebene
d) Tragen (horizontale Bewegung)
e) Beschleunigungsarbeit
f) Spannarbeit
1. Beispiel: Zunehmende Kraft
2. Hubarbeit
a) Beschreibung
F
F(s)
Fmax
W = ½  so  Fmax
so
Der Faktor ½ spielt bei
Kräfteparallelogrammen
öfter eine Rolle, wenn
die Kraft linear steigt.
s
Ein Körper der Masse m wird um die Höhe h angehoben.
Je größer die Masse m,
desto mehr Kraft wird
benötigt  die Arbeit
wird größer.
b) vertikales Heben
m
h
m
Aufgabe: Zeichne alle wirkenden Kräfte ein!
Lösung:
Gewichtskraft : FG = -m  g
m
h
FH
Hubkraft:
FH = m  g
Hubhöhe:
h
Hubarbeit:
WH = m  g  h
m
FG
FH ist nur beim Start größer
 nach Newton:
Wenn keine aüßere Kräfte
einwirken, sind beide Kräfte
gleich groß
 beim Heben sind FH
und FG gleich groß.
c) Schiefe Ebene
Eine Masse m wird über eine Schiefe Ebene mit Neigungswinkel  und die
Höhe h gehoben.
FZ
Die Schenkel sind
paarweise senkrecht zu
dem Dreieck der
Schiefen Ebene
 Der Winkel  ist im
Kräfteparallelogramm
gleich groß.
FH
s

FG
h

Aufgabe: Wie hängt FZ oder FH mit dem Winkel  zusammen?
Lösung:
sin() =
FH
=
FG
h
s
h
FH = FG  sin() ; s =
sin()
h
W = FH  s = FG  sin() 
sin()
W = FG  h
Schlussfolgerung:
Physikalisch ist die Arbeit an der Schiefen Ebene gleich dem vertikalen Heben
um die gleiche Höhe.
d) Tragen (horizontale Bewegung)
FH
FH
m
m
FG
FG
h
s
W
= F  s  cos()
= m  g  s  cos(90°)
=mgs0
=0
Ein Physiker würde das nicht glauben!
 aber das Ergebnis stimmt, wenn man
von der Reibung absieht und die
Beschleunigung schon vorbei ist ( Luft –
kissenfahrbahn), sonst braucht man noch
andere Faktoren.
e) Beschleunigungsarbeit
Ein Körper mit der Masse m wird von 0 auf eine Geschwindigkeit vo
beschleunigt
v=
m
FZ
m
2a  s
v
v2
0
s=
s
W = FZ  s
v
W=ma
2
v
= m
2a
1
WB =
2

m  v2
2
2a
2a
FZ = m  a
f) Spannarbeit
Eine Feder wird um die zusätzliche Länge s verlängert.
0
s
0+s
Aufgabe: Trage alle wirkenden Kräfte ein (keine Masse)!
Lösung:
0
FD
s
0+s
FZ
FD
FZ = - FD
FD(s)
FD = ½ D  s
FDmax
W = ½  so  Fmax
Der Graph steigt linear
 FD  D  s, sondern
½  D  s (Die Kraft ist
am Anfang kleiner und
steigt linear)
s
so
WD = FZ  s
=½Dss
= ½  D  s2
Da die Kraft linear ansteigt (längs des Weges) ergibt das Arbeitsdiagramm eine
Dreiecksfläche:
WD = ½  D  s2
Aufgabe:
Eine Schraubenfeder wird durch eine Kraft F = 0,6 N um s = 3,5 cm gedehnt.
Wie groß ist die Spannarbeit, um die Feder um weitere 7,0 cm auszuziehen?
Geg.: F1 = 0,6 N ; s1 = 3,5 cm ; s2 = 7 cm
Ges.: W12
Arbeit von
Zustand 1 nach
Zustand 2
Lös.: WD = ½  D  s2
D =
FD
s
=
0,6 N
0,035 m
= 17 1/7
N
m
W12 = W2 – W1
= ½  D  s22 – ½  D  s12
N
2
2
= ½  17 1/7
 (0,0049 m – 0,001225 m )
m
= 8 4/7
N

0,003675 m2
m
= 0,0315 Nm
Antwort:
Die Spannarbeit ist 0,0315 Nm groß, um die Feder um weitere 7 cm
auszuziehen.