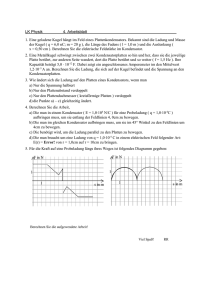
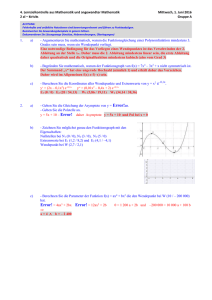
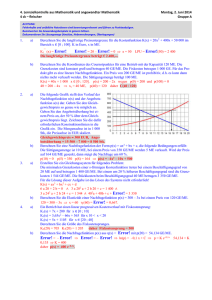
3. Schriftliche Wiederholung aus Physik Donnerstag, 27. Februar 1997

5. Lernzielkontrolle
4 ck – kircher
1.
Mittwoch, 9. Juni 2010
Gruppe A
Ausführung
Berechnen Sie eine Nachfragefunktion aus dem Verlauf der Elastizität (x) = Error!. Bei einem Preis 200
GE/ME können 60 ME abgesetzt werden. Wie hoch ist der maximale Erlös?
Es liegt eine lineare Kostenfunktion vor. Wie hoch sind die konstanten Grenzkosten, wenn die Cournotmenge
xc = 30 ME beträgt?
Error! = – Error!  Error! = Error!  ln p = ln (x – 80) + C  p = K(x – 80) mit p(60) =
200 
200 = K(60 – 80)  K = – 10  p(x) = 800 – 10x
Maximaler Erlös:
(x) = 1  80 – x = x  x = 40 p(40) = 400 GE/ME Emax (40) = 400 GE/ME · 40 ME = 16.000 GE/ME
K(x) = ax + b
Error! = Error!(800x – 10x2) = 800 – 20x
Error! = a = 200
2.
Error!(30) = 800 – 20 · 30 =
Berechnen Sie eine Nachfragefunktion aus dem Verlauf der Elastizität (x) = Error! . Bei einem Preis von
110,36 GE/ME können 10 ME abgesetzt werden.
Error! = – Error!  Error! = –0,1 dx  ln p = –0,1 x + C  p = K e–0,1x mit p(10) = 110,36

110,36 = K e–1  K = 300  p(x) = 300 e–0,1x
3.
Berechnen Sie eine Nachfragefunktion aus dem Verlauf der Elastizität (x) = Error! mit dem Maximalpreis
89,4.
Error! = – Error!  Error! = Error!  ln p = lnError! – lnError!+ C
ln p = ln
Error! für x  30  p(x) = K Error!
89,4 = p(0) = 8,94 K  K = 10 daher p(x) = 10 Error! = Error!
4.
Von einer linearen Nachfragefunktion kennt man den Prohibitivpreis 1.000 GE/ME. Die Elastizität an der Stelle
x = 50 beträgt 3. Berechnen Sie die Gleichung der Nachfragefunktion. Um welchen Prozentsatz ändert sich der
Erlös, wenn man beim Absatz 50 ME den Preis um 10 % senkt?
p(x) = ax + b
(x) = Error!
daher
p(0) = 1.000 = b
(50) = 3  3 · 50 a = – (50a + b)  –200a = b  a = – Error! = – 5
p(x) = 1.000 – 5x
 = – Error!  rel. Abs.änd. = –  · rel. Preisänd. = – 3 · (–0,1) = 0,3
rel Erlösänderung = 0,9 · 1,3 = 1,17 also um 17 % höher
oder
p(50) = 750 daher E(50) = 37.500
daher E(65) = 43.875 d.s. + 17 %
675 = 1000 – 5x  x = 65
5. Lernzielkontrolle
4 ck – kircher
1.
Mittwoch, 9. Juni 2010
Gruppe B
Ausführung
Berechnen Sie eine Nachfragefunktion aus dem Verlauf der Elastizität (x) = Error!. Bei einem Preis 200
GE/ME können 40 ME abgesetzt werden. Wie hoch ist der maximale Erlös?
Es liegt eine lineare Kostenfunktion vor. Wie hoch sind die konstanten Grenzkosten, wenn die Cournotmenge
xc = 10 ME beträgt?
Error! = – Error!  Error! = Error!  ln p = ln (x – 60) + C  p = K(x – 60) mit p(40) =
200 
200 = K(40 – 60)  K = – 10  p(x) = 600 – 10x
Maximaler Erlös:
(x) = 1  60 – x = x  x = 30 p(30) = 300 GE/ME Emax (40) = 300 GE/ME · 30 ME = 9.000 GE/ME
K(x) = ax + b
Error! = Error!(600x – 10x2) = 600 – 20x
Error! = a = 400
2.
Error!(30) = 600 – 20 · 10 =
Berechnen Sie eine Nachfragefunktion aus dem Verlauf der Elastizität (x) = Error! . Bei einem Preis von
147,15 GE/ME können 5 ME abgesetzt werden.
Error! = – Error!  Error! = –0,2 dx  ln p = –0,2 x + C  p = K e–0,2x mit p(5) = 147,15

147,15 = K e–1  K = 400  p(x) = 400 e–0,1x
3.
Berechnen Sie eine Nachfragefunktion aus dem Verlauf der Elastizität (x) = Error! mit dem Maximalpreis
22,36.
Error! = – Error!  Error! = Error!  ln p = lnError! – lnError!+ C
ln p = ln
Error! für x  20  p(x) = K Error!
22,36 = p(0) = 2,236 K  K = 10 daher p(x) = 10 Error! =
4.
Error!
Von einer linearen Nachfragefunktion kennt man den Prohibitivpreis 1.000 GE/ME. Die Elastizität an der Stelle
x = 50 beträgt 4. Berechnen Sie die Gleichung der Nachfragefunktion. Um welchen Prozentsatz ändert sich der
Erlös, wenn man beim Absatz 50 ME den Preis um 10 % senkt?
p(x) = ax + b
(x) = Error!
daher
p(0) = 1.000 = b
(50) = 4  4 · 50 a = – (50a + b)  –250a = b  a = – Error! = – 4
p(x) = 1.000 – 4x
 = – Error!  rel. Abs.änd. = –  · rel. Preisänd. = – 4 · (–0,1) = 0,4
rel Erlösänderung = 0,9 · 1,4 = 1,26 also um 26 % höher
oder
p(50) = 800 daher E(50) = 40.000
daher E(70) = 50.400 d.s. + 26 %
5. Lernzielkontrolle
4 ck – kircher
1.
720 = 1000 – 4x  x = 70
Mittwoch, 9. Juni 2010
Gruppe A
Berechnen Sie eine Nachfragefunktion aus dem Verlauf der Elastizität (x) = Error!.
Bei einem Preis 200 GE/ME können 60 ME abgesetzt werden.
Wie hoch ist der maximale Erlös?
Es liegt eine lineare Kostenfunktion vor.
Wie hoch sind die konstanten Grenzkosten, wenn die Cournotmenge xc = 30 ME beträgt?
2.
Berechnen Sie eine Nachfragefunktion aus dem Verlauf der Elastizität (x) = Error! .
Bei einem Preis von 110,36 GE/ME können 10 ME abgesetzt werden.
3.
Berechnen Sie eine Nachfragefunktion aus dem Verlauf der Elastizität
(x) = Error!
mit dem Maximalpreis 89,4.
4.
Von einer linearen Nachfragefunktion kennt man den Prohibitivpreis 1.000 GE/ME.
Die Elastizität an der Stelle x = 50 beträgt 3.
Berechnen Sie die Gleichung der Nachfragefunktion.
Um welchen Prozentsatz ändert sich der Erlös, wenn man beim Absatz 50 ME den Preis um
10 % senkt?
5. Lernzielkontrolle
4 ck – kircher
Ausführung
Mittwoch, 9. Juni 2010
Gruppe B
1.
Berechnen Sie eine Nachfragefunktion aus dem Verlauf der Elastizität (x) = Error!.
Bei einem Preis 200 GE/ME können 40 ME abgesetzt werden.
Wie hoch ist der maximale Erlös?
Es liegt eine lineare Kostenfunktion vor.
Wie hoch sind die konstanten Grenzkosten, wenn die Cournotmenge xc = 10 ME beträgt?
2.
Berechnen Sie eine Nachfragefunktion aus dem Verlauf der Elastizität (x) = Error! .
Bei einem Preis von 147,15 GE/ME können 5 ME abgesetzt werden.
3.
Berechnen Sie eine Nachfragefunktion aus dem Verlauf der Elastizität
(x) = Error!
mit dem Maximalpreis 22,36.
4.
Von einer linearen Nachfragefunktion kennt man den Prohibitivpreis 1.000 GE/ME.
Die Elastizität an der Stelle x = 50 beträgt 4.
Berechnen Sie die Gleichung der Nachfragefunktion.
Um welchen Prozentsatz ändert sich der Erlös, wenn man beim Absatz 50 ME den Preis um
10 % senkt?