Versuch 10 - Michael Reinisch

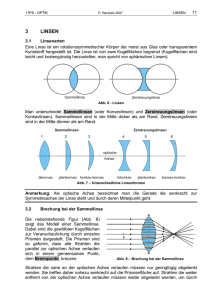
Versuch 10
Datum:
Ort:
Fach:
Gruppe:
10. Januar 2000
Protokollant:
Inhalt:
Michael Reinisch
Physikalisches Institut
Physikalisches Anfängerpraktikum Teil I Mechanik, Wärmelehre, Optik
Manon BETTINELLI
Matr.-Nr. 1569184
Michael REINISCH
Matr.-Nr. 1552900
1. Aufgabenstellung
2. Versuchsaufbau
3. Versuchsbeschreibung
 Dünne Linsen
 Linsensysteme
4. Versuchsergebnis
5. Fehlerbetrachtung
6. Zusatzaufgaben
Aufgabenstellung
Bestimmung der Brennweite einer Sammel- und einer Zerstreuungslinse sowie die Brennweite und Hauptpunktlage eines
Linsensystems.
Versuchsaufbau
G
F
F
Sammellinse
B
Sammellinse
Abb.1 F : Brennpunkt, G : Gegenstand, B : Bild (reell)
G
Z
B
Z
Zerstreuungslinse
Zerstreuungslinse
Abb.2 Z : Zerstreuungspunkt, G : Gegenstand, B : Bild (virtuell)
F1
F2
H2
H1
Sammellinse
Zerstreuungslinse
Sammellinse
Zerstreuungslinse
Abb.3 F2 : Brennpunkt, H1, H2 : Hauptebenen
B
G
F1
H1
F2
H2
Abb.4 F1, F2 : Brennpunkte, H1, H2 : Hauptebenen, G : Gegenstand, B : Bild (reell)
Versuchsbeschreibung
Dünne Linsen
Man unterscheidet zwei Arten von Linsen, Sammellinsen und Zerstreuungslinsen. Die Sammellinse bündelt die parallel zur
Symmetrieachse, auch optische Achse genannt, einfallenden Lichtstrahlen in einem Punkt, den Brennpunkt(siehe Abb.1). Die
meisten Linsen haben zwei Brennpunkte. Die Entfernung dieser Brennpunkte zur optischen Mittelebene nennt man Brennweite
f. Mit einer Sammellinse kann man ein reelles Bild eines Gegenstandes auf einen Schirm abbilden(siehe Abb.1). Die
Beziehung zwischen den Abständen des Gegenstandes und des Bildes zur Linse und der Brennweite läßt sich in folgender
Formel ausdrücken:
1/f = 1/g + 1/b mit g: Entfernung Gegenstand zur Linse und b: Linse zum Bild. Das Verhältnis von Bildgröße B zu
Gegenstandsgröße G nennt man Vergrößerung V:
V = B/G = b/g . Es lassen sich auch virtuelle Bilder wie bei der Zerstreuungslinse (siehe unten) erzeugen.
Die Zerstreuungslinse macht parallel zur optischen Achse einfallende Strahlen divergent und alle andern noch divergenter,
man sagt sie zerstreut das Licht(siehe Abb.2). Es scheint als kämen die Lichtstrahlen (für parallel Strahlen) aus einem Punkt,
den Zerstreuungspunkt. Umgekehrt erhält man paralleles Licht, wenn man eine Lichtquelle in den Zerstreuungspunkt stellt. Mit
Zerstreuungslinsen lassen sich nur virtuelle Bilder erzeugen. Unser Auge macht aus diesen wieder reelle Bilder und dadurch
sichtbar. Dabei erscheint der Gegenstand hinter der Linse in die Ferne gerückt(siehe Abb.2).
Zur Bestimmung der Brennweite der Sammellinse erzeugen wir ein „scharfes“ reelles Bild und messen g und b aus. Bei der
Zerstreuungslinse nutzen wir eine Eigenschaft von Linsensystemen aus. Durch hinzufügen einer Sammellinse läßt sich mit dem
entstehenden System wieder ein reelles Bild erzeugen und die Brennweiten verhalten sich wie folgt:
1/fa = 1/f1 + 1/f2 - D/ f1* f2 mit fa : Gesamtbrennweite, f1 , f2 : Brennweiten der beiden Linsen, D : Abstand zwischen der
Linsen(hier vernachlässigbar). Die Brechkraft läßt sich leicht bestimmen, da sie als Inverses der Brennweite definiert ist.
Abweichungen von den oben beschriebenen Eigenschaften der Linsen, d.h. Linsenfehler, nennt man Aberration. Da die
Brechzahl n() des Linsenmaterials (siehe auch Versuch 12/3 Dispersion) von der Wellenlänge  des Lichtes abhängt, ist (x)
die Brennweite f() der Linse für verschiedene Farben unterschiedlich groß. Diese Eigenschaft heißt chromatische Aberration
und läßt sich dadurch beheben, daß man ein Linsensystem aus zwei Linsen mit unterschiedlichen n() benutzt. Die
sphärische Aberration entsteht durch die Krümmung der Linse, was zur Folge hat, daß achsferne Strahlen stärker gebrochen
werden als achsennahe. Dies kann man umgehen indem man Randstrahlen nicht betrachtet (und) oder dünne Linsen benutzt
(wie im Versuch geschehen).
Linsensysteme
Das Linsensystem wirkt wie eine virtuelle Sammellinse, die, je nach Brennpunkt F1 oder F2, in der Ebene H1 oder H2 liegt(siehe
Abb.3). Diese Ebenen, Hauptebenen genannt, können auch außerhalb des Linsensystems liegen. g und b werden in Bezug
auf die entsprechenden Hauptebenen angegeben. Die Strahlen können außerhalb der Hauptebenen genauso wie bei dünnen
Linsen betrachtet werden, dazwischen als parallel(siehe Abb.4).
Versuchsergebnis
g [cm]
82,05
64,5
38,6
87,65
100,25
b [cm]
26,05
29,5
40,4
26,35
24,75
< f > = 19,973 cm
f [cm]
19,7725
20,2420
19,7397
20,2595
19,8495
1/f
0,0506
0,0494
0,0507
0,0494
0,0504
Zerstreuungslinse
g [cm] b [cm]
f(a)
95,1
34,9 11,2053
77,65 37,35 11,1449
52,75 47,25 11,0869
106,8 33,2 11,1658
87,45 35,55 11,1658
f(1)=19,97
1/f(2)
0,0392
0,0397
0,0401
0,0395
0,0395
f(2)
25,5307
25,2194
24,9244
25,3269
25,3269
< f > = 11,154 cm
Linsen-System
e(1) [cm] e(2) [cm] e(3) [cm] e(4) [cm] L [cm]
V
l
16,9
33,65
113,1
96,35
8,375 5,3846 19,3499
g
b
f
5,9251 85,3751 5,5405
Fehlerbetrachtung
Durch Ablesegenauigkeit und Ablesefehler bekommt man folgende Abweichungen:
g = 0,2 cm und b = 0,4 cm
1 / f = (1 / g) + (1 / b) => f = sqrt((g4 * g2 + b4 * b2) / ((b + g)4))
 < f > = 0,117 für die Sammellinse
 Sammellinse: f = 19,973 cm  0,059 cm
für die Zerstreuungslinse: g
= 0,8 cm und b = 0,9 cm
1 / f2 = 1 / fa - 1 / f1 => f = sqrt(fa4 * (b2 * g2 + g4 * b2) / ((-f1 + fa)4 * (b + g)4) + f14 * f12 /
((-f1 + fa)4))
 < f > = 0,915
 Zerstreuungslinse: f = 11,154 cm  0,458 cm
Zusatzaufgaben
G
F
B
Sammellinse
g>f
B
G
F
Sammellinse
g=f
B
G
F
Sammellinse
g<f

Im Fall g > f entsteht ein reelles Bild, daß umgekehrt ist und bei 2 * g = f gleich groß wie der Gegenstand G ist. Bei größer
werdenden g wird B kleiner und umgekehrt.

Im Fall g = f ist kein Bild zu sehen, da es in der optischen Mittelebene liegt.

Im Fall g < f entsteht ein virtuelles Bild, das bei 2 * g = f gleich groß wie G ist. Bei größer werdenden g wird B größer und
umgekehrt. Bei dieser Anwendung wird die Sammellinse als Lupe bezeichnet.
G
Z
B
Zerstreuungslinse
g>f
G
B
Z
Zerstreuungslinse
g=f
Z
GB
Zerstreuungslinse
g<f
Es entsteht ein virtuelles Bild, daß bei g = f genau halb so groß wie G ist. Bei größer werdenden g wird B kleiner und
umgekehrt.
n1
n1
n2
G
M1
M2
B1 = G2
b1
g1
b2
r2
g2
B2
r1
d
Wenn man die Linse als zwei gekrümmte Flächen betrachtet, bekommt man geometrisch

für die Abbildung durch die erste Fläche: (n1
/ g) + (n2 / b1) = (n2 - n1) / r1

für die Abbildung durch die zweite Fläche: (n2

durch Addition der beiden Gleichungen und mit d = g2 + b1 : (n1
/ g2) + (n1 / b2) = (n1 - n2) / r2
/ g) + (n1 / b2) + (n2 / b1) + (n2 / (d - b1)) =
(n2 - n1) * ((1 / r1) - (1 / r2))

für dünne Linsen, d.h. d ->  : (n1
/ g) + (n1 / b2) = (n2 - n1) * ((1 / r1) - (1 / r2))

mit n1 / f = (n2 - n1) * ((1 / r1) - (1 / r2)) : (1
/ g) + (1 / b2) = 1 / f
Eine weitere Möglichkeit der Herleitung ist folgende:
G
B
F
vereinfacht dargestellt:
f

G



B
g
b
F
Es gilt: tan()
= G / g = B / b und tan() = G / f = B / (b - f)
 B / G = b / g und B / G = (b - f) / f
 b / g = (b - f) / f
 b / g = (b / f) - 1
 (b / g) + 1 = b / f
 1 / f = ((b / g) / b) + (1 / b)
 1 / f = (1 / g) + (1 / b)