Der lange Weg zu den Logarithmen- und Exponentialgesetzen. 1

Der lange Weg zu den Logarithmen- und Exponentialgesetzen.
1. Schritt: xn , n ∈ N, also eine natürliche Zahl (ungleich Null). Wie jeder weiß
gilt:
9
106 · 103 = |10 · 10 · 10{z
· 10 · 10 · 10} · 10
| · 10
{z · 10} = |10 · 10 · 10 · 10 · 10
{z · 10 · 10 · 10 · 10} = 10
6 Faktoren
3 Faktoren
6+3 = 9 Faktoren
Das gilt deshalb auch allgemein für jede reelle Zahl x ∈ R und natürliche Zahlen
m, n ∈ N :
xn · xm = x
. . x · x} · x
. . x · x} = x
· x · x . . . x · x} = xn+m
| · x .{z
| · x .{z
| · x . . . x · x{z
n Faktoren m Faktoren
n+m Faktoren
(1)
Eine weitere Folgerung ist, dass gilt
xnm = (xn )m = xn · xn . . . xn = x
. . x · x} · |x · x .{z
. . x · x} . . . |x · x .{z
. . x · x}
| · x .{z
n Faktoren n Faktoren
n Faktoren
= |x · x . . . x · x · x · x . .{z
. x · x . . . x · x . . . x · x} = xnm
n mal m Faktoren
2. Schritt: Was gilt für rationale Zahlen r =
m
n
mit m, n ∈ N?
1
Wir beginnen mit der Definition von x n .
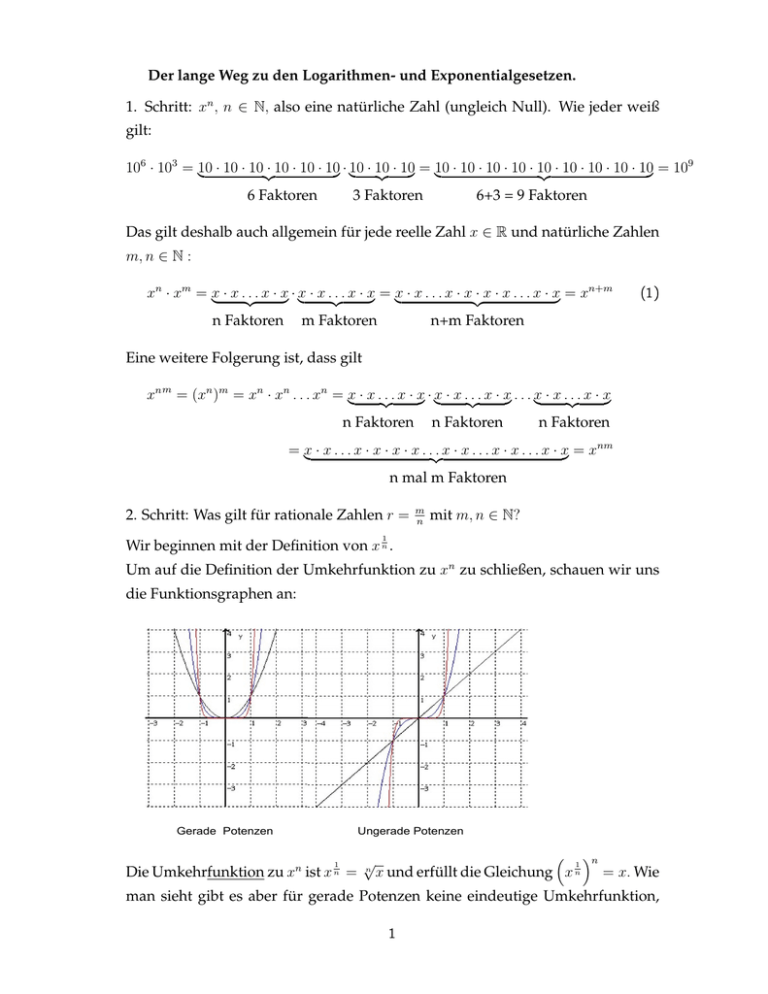
Um auf die Definition der Umkehrfunktion zu xn zu schließen, schauen wir uns
die Funktionsgraphen an:
Gerade Potenzen
Ungerade Potenzen
1
Die Umkehrfunktion zu xn ist x n =
1 n
√
n
x und erfüllt die Gleichung x n = x. Wie
man sieht gibt es aber für gerade Potenzen keine eindeutige Umkehrfunktion,
1
deshalb definiert man die Umkehrfunktion nur für nichtnegative Argumente.
Im Beispiel sieht das so aus:
1
Die Gleichung x2 = 4 hat zwei Lösungen, nämlich 2 und −2. Wie soll also 4 2 =
√
√
4 bestimmt sein? Per Definition wird 4 = 2 bestimmt.
Für ungerade Potenzen, also z.B. im Fall x3 = 8, tritt dieses Problem nicht auf.
√
1
Trotzdem wird definiert, dass x 3 = 3 x nur für nichtnegative x definiert ist.
Dagegen ist aber die Gleichung x3 = −8 sehr wohl lösbar, sie hat die Lösung
√
x = − 3 8 = −2.
Es gilt somit die Definition
1 m
√
m
n
= ( n x)m ,
x = xn
x ≥ 0,
n, m ∈ N.
3. Schritt: Per Definition ist x0 = 1 für alle x ∈ R.
4. Schritt: Negative, ganze Zahlen −n, n ∈ N.
Für x 6= 0 gilt x ·
1
x
= 1 und damit auch
n
xn
1
1
n
= 1 = n = xn n .
x ·
x
x
x
Deshalb definiert man x−n :=
1
,
xn
was auch sehr gut zu (1) passt, da gilt
xm · x−n =
xm
= xm−n .
xn
5. Schritt: Was ist eine sinnvolle Definition für reelle Zahlen α ∈ R? Wie sollte
man xα definieren? Dazu bedient man sich der sogenannten e-Funktion mit der
Eulerschen Zahl e.
6. Schritt: Die e-Funktion und die Logarithmusfunktion ln x. Für rationale und
ganzzahlige Exponenten q ist eq nach den bisherigen Überlegungen definiert.
D.h. es gilt
1 m
√
m
1
en+m = en · em ,
e n = en
= ( n e)m , e−n = n ,
e
1 −m
√
m
1
1
1
e− n = e n
= ( n e)−m = 1 m = √
= m.
n
m
( e)
en
en
(2)
(3)
Da jede irrationale Zahl durch rationale Zahlen approximiert werden kann, definiert
man nun die e-Funktion für irrationale Zahlen α wie folgt. Es sei rn eine Folge
rationaler Zahlen mit limn→∞ rn = α, dann ist
eα := lim ern .
n→∞
2
Bildlich: Stellen Sie sich vor, dass für alle rationalen und negativen rationalen
Zahlen q die Werte eq berechnet sind. Dann können diese Paare (q, eq ) im xy-Koordinatensystem eingetragen werden, die Werte für eα ergeben sich dann
durch "zudefinieren" indem die "Linie" durchgezogen wird. Auf diese Weise wird
eine stetige Funktion ex für alle reellen x erklärt und es gelten die Exponentialgesetze (genauso wie vorher (2)):
eα+β = eα · eβ ,
für alle reellen α, β ∈ R.
Insbesondere ist
eα
1
α−β
α
−β
und
e
=
e
·
e
=
.
eα
eβ
Damit haben wir für den Spezialfall x = e die Funktion xα erklärt. Wie kommt
e−α =
aber nun allgemein auf xα . Dazu schauen wir uns die Funktion eα an:
y=exp  x=e
x
y=ln  x
Exponentialfunktion (schwarz), Logarithmusfkt. (blau)
Offensichtlich gibt es eine Umkehrfunktion und diese wird mit ln x bezeichnet,
d.h.
y = ln x ⇐⇒ ey = x.
Das hat als erstes die Konsequenz, dass der Definitionsbereich des natürlichen
Logarithmus alle positiven reellen Zahlen sind, da dies der Wertebereich der eFunktion ist.
Weiterhin ergeben sich die Logarithmengesetze aus den Potenzgesetzen:
Sei y1 = ln x1 , y2 = ln x2 ,
y1 , y1 , x1 , x2 ∈ R, x1 , x2 > 0, dann gilt ey1 = x1 und
ey2 = x2 und wir erhalten:
x1 · x2 = ey1 · ey2 = ey1 +y2 ⇐⇒ ln(x1 · x2 ) = ln e(y1 +y2 ) = y1 + y2 = ln x1 + ln x2 ,
3
und
x1
ey1
= y2 = ey1 −y2 ⇐⇒ ln
x2
e
x1
x2
= ln e(y1 +y2 ) = y1 − y2 = ln x1 − ln x2
sowie für n ∈ N :
xn1 = (ey1 )n = e(ny1 ) ⇐⇒ ln xn1 = ln e(ny1 ) = n y1 = n ln x1 .
7. Schritt: Nun können wir xα für x > 0 wie folgt definieren:
xα = eln(x
α)
= eα ln(x) .
Bemerkung: Anstelle der Basis e hätte man auch andere positive reelle Zahlen
ungleich 1 verwenden können, von Bedeutung sind insbesondere die Zahl 2 bzw.
die Zahl 10 als Basis. Der Logarithmus bzgl. der Basis 2 wird auch mit ld (x) und
der Logarithmus zur Basis 10 wird auch mit lg x bezeichnet.
Man kann sich die Exponentialgesetze auch so merken, dass sich die Exponenten
addieren, wenn man Potenzen zur gleichen Basis (also z.B. 10 oder eben auch e)
multipliziert.
Vorsicht Falle: Die Funktion ln x2 ist für alle reellen x mit x 6= 0 definiert, aber
ln x2 = ln |x|2 = 2 ln |x|, dagegen ist die Funktion 2 ln x nur für positive reelle x
definiert!
4