Kräfte am Keil
Werbung
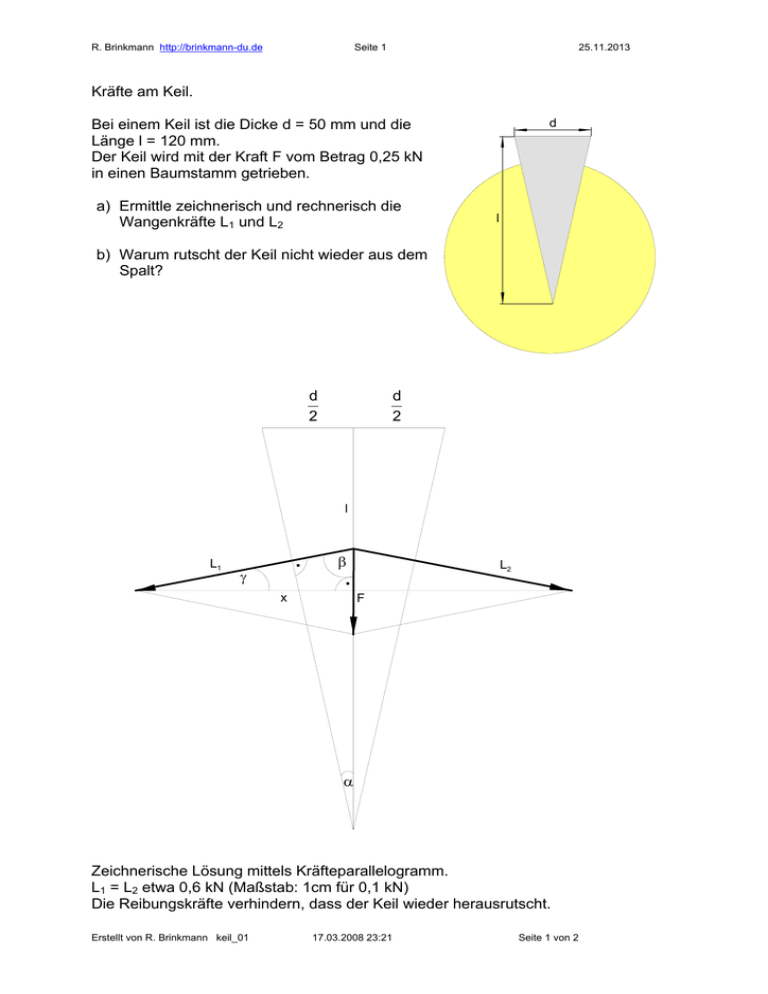
R. Brinkmann http://brinkmann-du.de Seite 1 25.11.2013 Kräfte am Keil. d Bei einem Keil ist die Dicke d = 50 mm und die Länge l = 120 mm. Der Keil wird mit der Kraft F vom Betrag 0,25 kN in einen Baumstamm getrieben. a) Ermittle zeichnerisch und rechnerisch die Wangenkräfte L1 und L2 l b) Warum rutscht der Keil nicht wieder aus dem Spalt? d 2 d 2 l L1 β γ x L2 F α Zeichnerische Lösung mittels Kräfteparallelogramm. L1 = L2 etwa 0,6 kN (Maßstab: 1cm für 0,1 kN) Die Reibungskräfte verhindern, dass der Keil wieder herausrutscht. Erstellt von R. Brinkmann keil_01 17.03.2008 23:21 Seite 1 von 2 R. Brinkmann http://brinkmann-du.de Seite 2 25.11.2013 Rechnerische Lösung: Die Wangenkräfte wirken senkrecht zu den Keilkanten. Aus Symmetriegründen teilt sich die Kraft F in zwei gleich große Wangenkräfte L1 und L2 auf. Der Keil selber stellt ein gleichschenkliges Dreieck mit der Basis d und der Höhe l dar. Eine Betrachtung der Winkel ergibt: β = 900 − α ( und damit d F | ⋅2 = 2⋅l 2⋅ x d F ⇔ = | ⋅x l x d l ⇔ ⋅x =F|⋅ l d l ⇔ x = ⋅F d ) γ = 900 − β = 900 − 900 − α = α also γ = α d d tg ( α ) = 2 = l 2⋅l wegen γ = α gilt auch F F tg ( α ) = 2 = x 2⋅x Nach dem Satz von Pythagoras gilt: 2 2 1 ⎛l⎞ ⎛F⎞ ⎛ l ⎞ L1 = ⎜ ⎟ + ⎜ ⎟ ⋅ F2 = F ⋅ + 4 ⎜⎝ d ⎟⎠ ⎝ 2⎠ ⎝ d⎠ Erstellt von R. Brinkmann keil_01 2 ⇒ L1 = L 2 = 0,25 kN ⋅ 17.03.2008 23:21 1 120 mm + ≈ 0,612kN 4 50 mm Seite 2 von 2