Physikalische Größen und Einheiten
Werbung
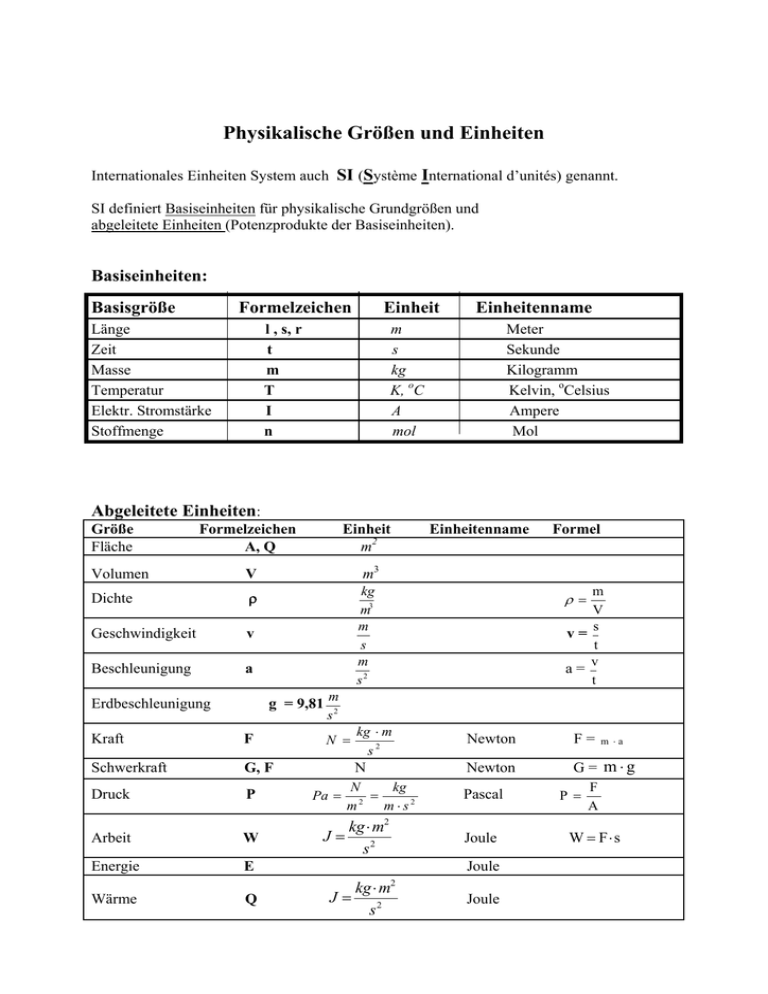
Physikalische Größen und Einheiten Internationales Einheiten System auch SI (Système International d’unités) genannt. SI definiert Basiseinheiten für physikalische Grundgrößen und abgeleitete Einheiten (Potenzprodukte der Basiseinheiten). Basiseinheiten: Basisgröße Formelzeichen Länge Zeit Masse Temperatur Elektr. Stromstärke Stoffmenge Einheit l , s, r t m T I n Einheitenname m s kg K, oC A mol Meter Sekunde Kilogramm Kelvin, oCelsius Ampere Mol Abgeleitete Einheiten: Größe Fläche Formelzeichen A, Q Einheit m2 Volumen V m3 Dichte ρ Geschwindigkeit v Beschleunigung a kg m3 m s m s2 Erdbeschleunigung g = 9,81 Kraft F Schwerkraft G, F Druck P Arbeit W Energie E Wärme Q Einheitenname Formel m V s v= t v a= t ρ= m s2 N = Pa = kg ⋅ m s2 Newton F= N Newton G = m⋅g N kg = 2 m m ⋅ s2 kg ⋅ m2 J= s2 Pascal Joule Joule J= kg ⋅ m s2 2 Joule P= m ⋅a F A W = F⋅s W= J kg ⋅ m2 = s s3 Watt Volt Leistung P Spannung U V Elektr. Widerstand R V ( ohm ) = A Ladung Q Kapazität C α, β, γ, ... Winkel Frequenz f, ν Kreisfrequenz ω C = A⋅ s F = C V rad 1 s 1 rad ⋅ s Hz = Bogenmaß eines Winkels Das Bogenmaß eines Winkels α ist definiert als das Verhältnis der Länge des Kreisbogens b zum Radius r. b α= r Für den Einheitskreis (r = 1) ist das Bogenmaß gleich der Länge des Kreisbogens b. Das Bogenmaß ist also eine dimensionslose Zahl mit dem Einheitenzeichen „rad“ (Radiant). Ist die Bogenlänge gleich dem Radius ( b = r ), so ist der Winkel 1 rad. Das Verhältnis Kreisumfang zu Radius ist 2π . Der Vollwinkel (360°) beträgt daher im Bogenmaß 2π rad . 180° sind π rad 90° sind 1° ist π 2 π 180 rad rad P= W t U I Q = I⋅t Q C= U R= Ohm Coulomb Farad Radiant Hertz f = 1 T (Periodendauer) ω = 2π ⋅ f