4. analytische geometrie - im Mathematik

157
4. ANALYTISCHE GEOMETRIE
Lernfeld: Wo ist was im Raum?
212
1. Achtung: Korrektur in der 2. Auflage.
Richtig sollte es lauten: Der Punkt C liegt 210 cm hoch.
• 210 − 80 − 85 = 45
Der Hängeschrank hat einen Abstand von etwa 45 cm zur Arbeitsplatte.
• zu A: x1 -Koordinate aus Grundriss mit P als Referenz bestimmen:
x1 ≈ 84 cm. x 2 und x 3 wie bei P; A(84 | 60 | 85)
zu B: Koordinaten aus Grundriss; B(38 | 106,5 | 130)
zu C: C(60 | 190 | 210)
• Abstand im Grundriss ≈ 84 cm. Höhenunterschied: 45 cm.
AB = (84 cm) 2 + (45 cm) 2 ≈ 95,3 cm
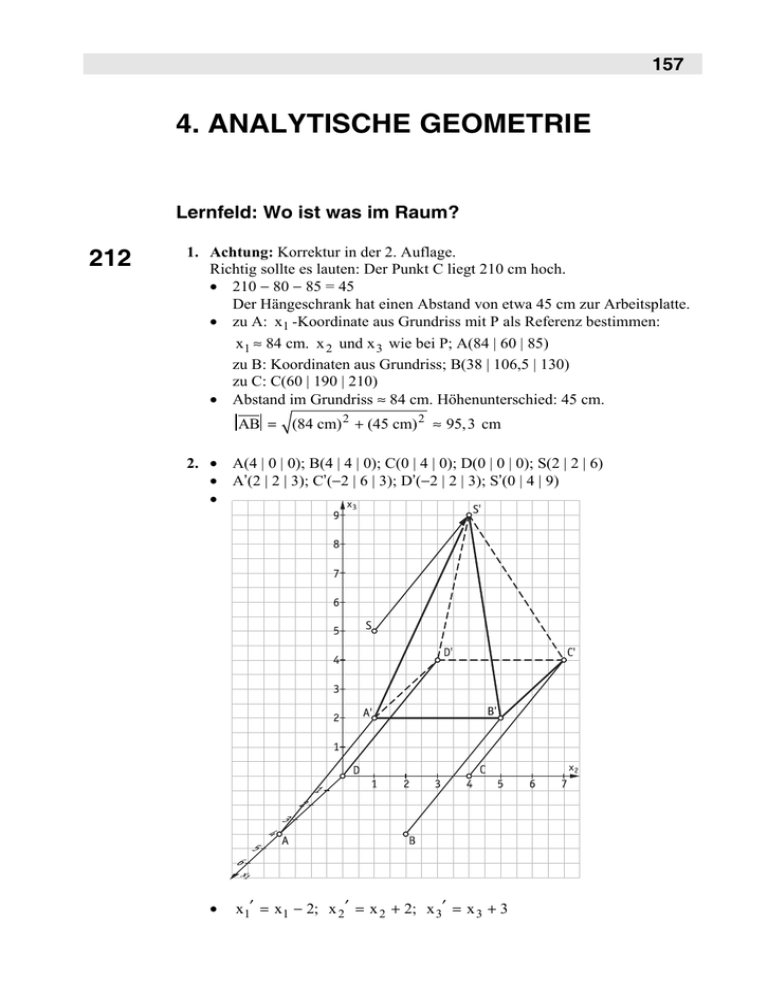
2. • A(4 | 0 | 0); B(4 | 4 | 0); C(0 | 4 | 0); D(0 | 0 | 0); S(2 | 2 | 6)
• A’(2 | 2 | 3); C’(−2 | 6 | 3); D’(−2 | 2 | 3); S’(0 | 4 | 9)
•
•
x1′ = x1 − 2; x 2′ = x 2 + 2; x 3′ = x 3 + 3
158
213
3. • Durch die weitere Raumdimension ist es möglich, dass Geraden
„aneinander vorbeilaufen“. D. h. sie schneiden sich nicht, obwohl sie
nicht parallel sind. Dies ist in der Ebene nicht möglich. Solche Geraden
nennt man windschief zueinander.
• In der Aufgabe 2 wurde bereits ein räumliches Koordinatensystem und
die Beschreibung einer Verschiebung im Raum erarbeitet.
Mit diesen Ideen könnte man z. B. den Punkt B als Bildpunkt einer Verschiebung des Punktes A deuten: A(3 | 5 | 3) → B(3 − 2 | 5 + 2 | 3 − 2) .
Alle Punkte X AB der Strecke AB kann man beschreiben durch
X AB (3 − k | 5 + k | 3 − k) mit k ∈ [ 0; 2] für k ∈ \ wird die Gerade
durch die Punkte A und B beschrieben.
• Für die Gerade durch C und D ergibt sich entsprechend
X CD (1 | 4 + t | 1 + t) mit t ∈ \.
Rechnerisch kann man nachweisen, dass die beiden Geraden keine
gemeinsamen Punkte haben. Wenn es einen gemeinsamen Punkt geben
würde, so müsste seine erste Koordinate 1 sein, da die erste Koordinate
aller Punkte auf der Geraden CD 1 ist.
Nur für k = 2 ist die erste Koordinate eines Punktes der Geraden AB 1;
man erhält dann den Punkt B(1 | 7 | 1) als möglichen Schnittpunkt.
B(1 | 7 | 1) liegt jedoch nicht auf der Geraden CD, da es keinen Wert für
t gibt, sodass 4 + t = 7 und 1 + t = 1 erfüllt sind.
4. • A(0 | 0); B(2 | 1); C(−2 | 4)
A(0 | 0); B’(−4 | −2); C’(1,5 | −3)
A(0 | 0); B’’(1 | 3); C’’(−4,5 | 1,5)
• Z. B. über Pythagoras: Seitenlängenquadrate betrachten
2
2
2
AB + AC = 5 + 20; BC = 16 + 9 = 25
2
2
2
AB′ + AC′ = 20 + 11, 25; B′C′ = 30, 25 + 1
2
2
2
AB′′ + AC′′ = 10 + 22,5; B′′C′′ = 30, 25 + 2, 25
• B(2 | 1); C( −2 | 4)
Beziehung: 2 ⋅ ( −2) + 1 ⋅ 4 = 0
• B′( −4 | −2); C′(1,5 | −3)
Beziehung: ( −4) ⋅ 1,5 + ( −2) ⋅ ( −3) = 0
• B′′(1 | 3); C′′( −4,5 | 1,5)
Beziehung: 1 ⋅ ( −4,5) + 3 ⋅ 1,5 = 0
Die Summe der Produkte aus den beiden x-Koordinaten und den beiden
y-Koordinaten ist gleich null.
4.1 Punkte und Vektoren im Raum
4.1.1 Punkte im räumlichen Koordinatensystem
217
2. a) P′(2 | 3 | 0)
b) x1x 3 -Ebene: (2 | 0 | 4)
x 2 x 3 -Ebene: (0 | 3 | 4)
159
217
2. c) Spiegelung an x1x 2 -Ebene: (2 | 3 | −4)
Spiegelung an x1x 3 -Ebene: (2 | −3 | 4)
Spiegelung an x 2 x 3 -Ebene: (−2 | 3 | 4)
3. Es muss immer einen definierten Anfangspunkt geben von dem aus Richtung und Entfernung angegeben werden.
Wählt man als Richtungen die Richtung der Wände und die Vertikale, erhält
man ein Standard-Rechtssystem.
Durch geschickte Wahl des Anfangspunkts lassen sich bestimmte Punkte
einfacher beschreiben als andere.
4. a)
A ′(6 | 0 | 0); B′(6 | 6 | 0); C′(0 | 6 | 0); D′(0 | 0 | 0); E ′(6 | 0 | 0);
F′(6 | 2 | 0); G ′(6 | 6 | 0); H ′(4 | 6 | 0); I′(0 | 6 | 0); K ′(0 | 0 | 0)
5. a)
160
217
5. b)
6. Lina hat das perspektivische Zeichnen der x1 -Achse beim Abtrag der x 2 und x 3 -Koordinaten missachtet und dementsprechend zu lang gezeichnet.
7. a) x1 -Koordinate: Null: x 2 x 3 -Ebene,
[ x 2 -Koordinate: Null: x1x 3 -Ebene,
x 3 -Koordinate: Null: x1x 2 -Ebene ]
b) Auf der x 3 -Achse .
c) Auf einer Ebene parallel zur x1x 2 -Ebene mit der x 3 -Koordinate 3.
d) Auf einer Geraden parallel zur x 3 -Achse durch den Punkt P(2 | 3 | 0).
8. Beispiel
Eckpunkte:
A(5 | 2,5 | 0); B(5 | 12,5 | 0); C(−5 | 2,5 | 0); D(−5 | 12,5 | 0); S(0 | 7,5 | 8)
161
218
9. a) Schrägbild siehe Schülerbuch; Wahl der Achsen wie auf S. 215
A(4 | 0 | 0); B(4 | 4 | 0); C(0 | 4 | 0); D(0 | 0 | 0); E(4 | 0 | 6); F(4 | 4 | 6);
G(0 | 4 | 6); H(0 | 0 | 6); S(2 | 2 | 9)
b) A(2 | −2 | 0); B(2 | 2 | 0); C(−2 | 2 | 0); D(−2 | −2 | 0); E(2 | −2 | 6);
F(2 | 2 | 6); G(−2 | 2 | 6); H(−2 | −2 | 6); S(0 | 0 | 9)
c) Die x 3 -Koordinaten sind gleich. Jeweils die x1 - und x 2 -Koordinate
ist bei a) um 2 Einheiten größer als bei b).
Dies entspricht gerade der Verschiebung von D zu M.
10. a) A = (17 | −15 | 0)
B = (17 | −15 | 8)
D = (0 | 0 | 8)
E = (0 | 22 | 8)
G = (−12 | 22 | 0)
H = (0 | 22 | 0)
J = (17 | 0 | 0)
b) x1 -x 2 -Ebene: A, G, H, I, J
C = (17 | 0 | 8)
F = (−12 | 22 | 8)
I = (0 | 0 | 0)
x 2 -x3 -Ebene: D, E, H, I
x1 -x3 -Ebene: C, D, I, J
c) A = (−17 | 37 | 0)
B = (−17 | 37 | 8)
D = (0 | 22 | 8)
E = (0 | 0 | 8)
G = (12 | 0 | 0)
H = (0 | 0 | 0)
J = (−17 | 22 | 0)
x1 -x 2 -Ebene: A, G, H, I, J
C = (−17 | 22 | 8)
F = (12 | 0 | 8)
I = (0 | 22 | 0)
x 2 -x3 -Ebene: D, E, H, I
x1 -x3 -Ebene: E, F, G, H
11. Aus der Darstellung eines 3-dimensionalen Koordinatensystems auf einer
2-dimensionalen Zeichenfläche kann man nicht eindeutig die Koordinaten
von Punkten ablesen, z. B. könnten die Punkte auch durch:
P(−2 | 2 | 1) und Q(1 | −2 | −1) beschrieben werden.
Erst durch weitere Informationen bzw. Lagebeziehungen kann Eindeutigkeit
erreicht werden.
(2) (−2 | −3 | −1,5)
(3) (0 | −2 | −0,5)
12. (1) (−3 | −3,5 | −2)
Da jeweils eine Koordinate gegeben ist, ist eine Ebene festgelegt und aus
der 2D-Darstellung sind die anderen Werte eindeutig ablesbar.
13. a) P′(−4 | 0 | 0); Q ′(0 | 3 | 0); R ′(3 | −2 | −4); S′(−8 | 5 | 3)
b) P'' (−4 | 0 | 0); Q'' (0 | −3 | 0); R'' (3 | 2 | 4); S'' (−8 | −5 | −3)
c) P''' (4 | 0 | 0); Q''' (0 | 3 | 0); R''' (−3 | −2 | 4); S''' (8 | 5 | −3)
d) P'''' (4 | 0 | 0); Q'''' (0 | −3 | 0); R'''' ( −3 | 2 | −4); S'''' (8 | −5 | 3)
162
4.1.2 Vektoren
219
2. Man kann jeden Vektor im Raum durch einen Quader mit den Seitenlängen
aus den Verschiebungskoordinaten darstellen.
Der Quader hat rechte Winkel, sodass die Länge des Vektors durch zweimalige Anwendung des Satzes des Pythagoras ausrechenbar ist:
d 2 = 5 2 + 7 2 = 74
G2
v = d 2 + (1,5) 2 = 76, 25
G
AA ′ = v = 76, 25 ≈ 8, 7
221
3. a) Richtung x1 -Achse:
Richtung x 2 -Achse:
5 Einheiten
7 Einheiten
Richtung x 3 -Achse:
1,5 Einheiten
Die Verschiebung auf G angewandt, ergibt G ′( −12 | 30,5 | 4).
b) Die Länge des Verschiebungspfeils von A nach A′ ist gleich der Länge
AA ′ der Raumdiagonalen im Koordinatenquader der Verschiebung
von A nach A′ .
Nach Pythagoras gilt
d 2 = 5 2 + 7 2 = 74
AA ′
2
= d 2 + 1,5 2 = 76, 25
⇒ AA ′ = 76, 25 ≈ 8, 7
Die Länge des Pfeils ist ca. 8,7 m.
4. a) Z. B.
163
221
4. b) A ′(−1 | 2 | 5)
c) B(−4 | 20 | −26)
G
d) Q um v verschoben gibt Q ′(8 | 11 | 4) ≠ P(8 | 11 | −4)
G
P ist kein Bildpunkt von Q unter v .
5. a) Q(9 | −6 | 24)
b) P(−3 | 13 | 18)
JJJG ⎛⎜ 4 ⎞⎟
6. a) DA = 0
⎜⎜ ⎟⎟
⎝0⎠
c) Q(−4 | −1 | −8)
d) P(q + 3 | q − 7 | 3q + 3)
JJJG ⎛⎜ 0 ⎞⎟
DC = 6
⎜⎜ ⎟⎟
⎝0⎠
JJJG ⎛⎜ −4 ⎞⎟
BC = 0
⎜⎜ ⎟⎟
⎝ 0⎠
JJJG ⎛⎜ 0 ⎞⎟
AB = 6
⎜⎜ ⎟⎟
⎝0⎠
JJJG ⎛⎜ 0 ⎞⎟
JJJG ⎛⎜ 4 ⎞⎟
JJJG ⎛⎜ 4 ⎞⎟
JJJG ⎛⎜ 0 ⎞⎟
CG = 0
HF = 6
DB = 6
EF = 6
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
4
0
0
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎝0⎠
JJJG JJJG
JJJG
JJJG
JJJG
b) DC; AB und EF bzw. HF und DB
JJJG ⎛⎜ 4 ⎞⎟ JJJG ⎛⎜ 4 ⎞⎟ JJJG ⎛⎜ 4 ⎞⎟ JJJG ⎛⎜ 0 ⎞⎟ JJJG ⎛⎜ 4 ⎞⎟ JJJG ⎛⎜ 0 ⎞⎟
c) OA = 0 ; OB = 6 ; OE = 0 ; OH = 0 ; OF = 6 ; OG = 6
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝0⎠
⎝0⎠
⎝4⎠
⎝4⎠
⎝4⎠
⎝4⎠
d) E, B, G, F
222
7. a) Es gibt 5 verschiedene Vektoren.
JJJG JJJG JJJG JJJG JJJG JJJG JJJG
AB = DE; AC; BC = EF; AD = CF =
JJJG JJG JJJG JJG JJJG JJJG JJJG JG
b) AC = JL ⎡⎣ AB = LI, BC = ED = GH = JI,
JJJG JJG
CG = DJ ⎤⎦
JJJG JJJG
BE; FD
JG JJJG JJJG JJJG
IJ = HG = DE = CB,
8. a) A ′(11 | 5 | 3)
b) A ′(10, 6 | 5, 4 | −10,9)
c) A ′(6 | 4 | −3)
⎛ 7⎞
G
G
9. a) v = ⎜ −6 ⎟ ; v = 101 ≈ 10, 05
⎜⎜ ⎟⎟
⎝ −4 ⎠
⎛ 19 ⎞
G
G
c) v = ⎜ −9 ⎟ ; v = 563 ≈ 23, 73
⎜⎜ ⎟⎟
⎝ 11 ⎠
⎛ 3⎞
G
G
b) v = ⎜ −4 ⎟ ; v = 34 ≈ 5,83
⎜⎜ ⎟⎟
⎝ 3⎠
⎛8⎞
G
G
d) v = ⎜ −8 ⎟ ; v = 192 ≈ 13,86
⎜⎜ ⎟⎟
⎝8⎠
10. a) b 3 = 7 oder b 3 = 3
b) a 2 = 0 oder a 2 = 6
d) A '(0 | 0 | 0)
c) b1 = 6 + 6; b1 = 6 − 6
d) b 2 = 23 oder b 2 = 19
164
222
11. Max hat die Koordinaten nicht quadriert.
Laura hat zwar die Beträge richtig quadriert aber übersehen, dass Quadrate
immer positiv sind, explizit (−2) 2 = (−2)(−2) = 4 .
12. a) beliebig viele
b) Man könnte für A und C beliebige Koordinaten wählen, die folgende
Bedingung erfüllen:
JJJG ⎛⎜ 2 − a1 ⎞⎟ ! JJJG ⎛⎜ c1 − 0 ⎞⎟ ⎛⎜ c1 ⎞⎟
AB = 4 − a 2 = OC = c 2 − 0 = c2
⎜
⎟
⎜
⎟ ⎜ ⎟
⎜0 −a ⎟
⎜c −0⎟ ⎜c ⎟
3⎠
⎝
⎝ 3
⎠ ⎝ 3⎠
4.1.3 Addition und Subtraktion von Vektoren
225
⎛1⎞ ⎛ 2 ⎞ ⎛1 + 2 ⎞ ⎛ 2 + 1⎞ ⎛ 2 ⎞ ⎛1⎞
2. (1) ⎜ 1 ⎟ + ⎜ 2 ⎟ = ⎜ 1 + 2 ⎟ = ⎜ 2 + 1 ⎟ = ⎜ 2 ⎟ + ⎜ 1 ⎟ ;
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟ ⎜⎜
⎟⎟ ⎜⎜
⎟⎟ ⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝1⎠ ⎝ 2 ⎠ ⎝1 + 2 ⎠ ⎝ 2 + 1⎠ ⎝ 2 ⎠ ⎝1⎠
genauso zu zeigen für den allgemeinen Fall:
⎛ a1 ⎞ ⎛ b1 ⎞ ⎛ a1 + b1 ⎞ ⎛ b1 + a1 ⎞ ⎛ b1 ⎞ ⎛ a1 ⎞
⎜a ⎟ +⎜b ⎟ = ⎜a + b ⎟ = ⎜b +a ⎟ = ⎜b ⎟ +⎜a ⎟
2⎟ ⎜ 2
2⎟ ⎜ 2⎟ ⎜ 2⎟
⎜ 2⎟ ⎜ 2⎟ ⎜ 2
⎜a ⎟ ⎜b ⎟ ⎜a + b ⎟ ⎜b +a ⎟ ⎜b ⎟ ⎜a ⎟
3⎠ ⎝ 3
3⎠ ⎝ 3⎠ ⎝ 3⎠
⎝ 3⎠ ⎝ 3⎠ ⎝ 3
⎛ 1 ⎞ ⎛ ⎛ 2 ⎞ ⎛ 3 ⎞ ⎞ ⎛ 1 + (2 + 3) ⎞ ⎛ (1 + 2) + 3 ⎞ ⎛ ⎛ 1 ⎞ ⎛ 2 ⎞ ⎞ ⎛ 3 ⎞
⎜
⎟
⎜
⎟
(2) ⎜ 1 ⎟ + ⎜ ⎜ 2 ⎟ + ⎜ 3 ⎟ ⎟ = ⎜ 1 + (2 + 3) ⎟ = ⎜ (1 + 2) + 3 ⎟ = ⎜ ⎜ 1 ⎟ + ⎜ 2 ⎟ ⎟ + ⎜ 3 ⎟ ;
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎜⎜
⎟⎟ ⎜⎜
⎟⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎜
⎟
⎜
⎟
⎝ 1 ⎠ ⎝ ⎝ 2 ⎠ ⎝ 3 ⎠ ⎠ ⎝ 1 + (2 + 3) ⎠ ⎝ (1 + 2) + 3 ⎠ ⎝ ⎝ 1 ⎠ ⎝ 2 ⎠ ⎠ ⎝ 3 ⎠
genauso zu zeigen für den allgemeinen Fall
⎛ 5 ⎞ JJJJG
G
3. a) Verschiebung v = ⎜ −1 ⎟ = AA ′ ; B′(7 | 3 | 6, 5); C′(7 | 2 | 4, 5)
⎜⎜
⎟⎟
⎝ 4, 5 ⎠
⎛ −2 ⎞ JJJJJG
G
b) 2. Verschiebung w = ⎜ −4, 5 ⎟ = A ′A ′′
⎜⎜
⎟⎟
⎝ −6 ⎠
165
225
⎛ 3 ⎞ JJJJG
G G G
3. c) gesamte Verschiebung u = v + w = ⎜ −5, 5 ⎟ = AA ′′
⎜⎜
⎟⎟
⎝ −1, 5 ⎠
226
4. a) C(0 | 2 | 7); D(3 | −1 | 2)
b) Seiten als Vektoren darstellbar:
JJJG ⎛ −5 ⎞
JJJG
AB = ⎜ 4 ⎟
AB = 66 ≈ 8,12
⎜⎜ ⎟⎟
⎝ 5⎠
JJJG ⎛ 2 ⎞
BC = ⎜ −3 ⎟
⎜⎜ ⎟⎟
⎝4⎠
JJJG ⎛ 3 ⎞
CD = ⎜ −3 ⎟
⎜⎜ ⎟⎟
⎝ −5 ⎠
JJJG ⎛ 0 ⎞
DA = ⎜ 2 ⎟
⎜⎜ ⎟⎟
⎝ −4 ⎠
JJJG
BC = 29 ≈ 5,38
JJJG
CD =
43 ≈ 6, 56
JJJG
DA = 20 ≈ 4, 47
166
226
5. a) A(5 | −6 | 0); B(5 | 6 | 0); C(−5 | 6 | 0); D(−5 | −6 | 0); E(5 | −6 | 4);
F(5 | 6 | 4); G(−5 | 6 | 4); H(−5 | −6 | 4); M(0 | −4 | 9); N(0 | 4 | 9)
JJJG ⎛ 0 ⎞ JJJG ⎛ −5 ⎞ JJJJG ⎛ −5 ⎞ JJJG ⎛ −5 ⎞ JJJG ⎛ −5 ⎞
b) AE = ⎜ 0 ⎟ ; FN = ⎜ −2 ⎟ ; MH = ⎜ −2 ⎟ ; FM = ⎜ −10 ⎟ ; AN = ⎜ 10 ⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜
⎟⎟
⎜⎜ ⎟⎟
⎝4⎠
⎝ 5⎠
⎝ −5 ⎠
⎝ 5 ⎠
⎝ 9⎠
⎛ 1 ⎞ ⎛ 3 ⎞ ⎛ −2 ⎞
e) ⎜ 2 ⎟ − ⎜ −1 ⎟ = ⎜ 3 ⎟
⎜ 4 ⎟ ⎜ −1 ⎟ ⎜ 5 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎛ −3 ⎞ ⎛ 6 ⎞ ⎛ −9 ⎞
f) ⎜ 2 ⎟ − ⎜ −8 ⎟ = ⎜ 10 ⎟
⎜ 1 ⎟ ⎜ −9 ⎟ ⎜ 10 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎛ 1 ⎞ ⎛ 5 ⎞ ⎛ −4 ⎞
g) ⎜ −2 ⎟ − ⎜ 4 ⎟ = ⎜ −6 ⎟
⎜ 3 ⎟ ⎜ −2 ⎟ ⎜ 5 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎛ −3 ⎞ ⎛ −7 ⎞ ⎛ 3 ⎞ ⎛ 1 ⎞
h) ⎜ 5 ⎟ − ⎜ −1 ⎟ − ⎜ −2 ⎟ = ⎜ 8 ⎟
⎜ −2 ⎟ ⎜ 3 ⎟ ⎜ −4 ⎟ ⎜ −1 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎛2⎞ ⎛ 1 ⎞ ⎛ 3⎞
6. a) ⎜ 3 ⎟ + ⎜ 4 ⎟ = ⎜ 7 ⎟
⎜ 5 ⎟ ⎜ −4 ⎟ ⎜ 1 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎛ 6 ⎞ ⎛ −9 ⎞ ⎛ −3 ⎞
b) ⎜ 9 ⎟ + ⎜ −5 ⎟ = ⎜ 4 ⎟
⎜3⎟ ⎜ 4 ⎟ ⎜ 7 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎛ 8 ⎞ ⎛ −6 ⎞ ⎛ 2 ⎞
c) ⎜ −5 ⎟ + ⎜ −1 ⎟ = ⎜ −6 ⎟
⎜ 3 ⎟ ⎜ −3 ⎟ ⎜ 0 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎛ −3 ⎞ ⎛ −1 ⎞ ⎛ 2 ⎞ ⎛ −2 ⎞
d) ⎜ 2 ⎟ + ⎜ −4 ⎟ + ⎜ 5 ⎟ = ⎜ 3 ⎟
⎜ −4 ⎟ ⎜ 6 ⎟ ⎜ −3 ⎟ ⎜ −1 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠
7. a)
x3
B
1200
1000
800
ZB
600
TB
Z
400
TZ
200
T
200
200
x1
400
JJJG ⎛ 1725 ⎞
TB = ⎜ 1649 ⎟
⎜ 2116 ⎟
⎝
⎠
JJJJJJG ⎛ 1237 ⎞
b) Z neu B = ⎜ 1115 ⎟
⎜ 1471 ⎟
⎝
⎠
400
600
800
1000
1200
x2
167
226
G G JJJG JJJG
8. a) a + b = AC = EG
G G JJJG JJJG
b) a − b = DB = HF
G G JJJG JJJG
c) b − a = BD = FH
G G JJJG JJJG
d) a − c = EB = HC
JJJG
G JJJG
9. AC = − u, AD =
JJJG
G G G
BD = − r − u + s,
JJJG
G G G
DB = − s + u + r,
227
G G JJJG JJJG
e) b + c = AH = BG
G G JJJG JJJG
f) b − c = ED = FC
G G G JJJG
g) a + b + c = AG
JJJG JJJG JJJG
G G
G
h) a − ( b + c ) = HG + GB = HB
G JJJG
G G
G G JJJG G G JJJG
− u + s, AE = r + t , BA = − r, BC = − r − u,
JJJG G G JJJG G G G JJJG
G G
CB = u + r, CE = u + r + t , DA = − s + u,
JJJG
G G G G
DE = − s + u + r + t
10. Die Überlegung ist falsch. Nach der Dreiecksregel kann man nur einen
inneren gemeinsamen Punkt streichen.
JJJG
JJJG
11. Gesucht ist b, sodass AB = AC
⎛ −1 ⎞
JJJG
AC = ⎜ −4 ⎟ = 21
⎜⎜ ⎟⎟
⎝ −2 ⎠
⎛ −4 ⎞
JJJG
AB = ⎜ b − 7 ⎟ = 17 + (b − 7) 2
⎜⎜
⎟⎟
⎝ −1 ⎠
JJJG
JJJG
AC = AB ⇔ 21 = 17 + (b − 7) 2 ⇔ b = 5 oder b = 9
12. A(0 | −5 | 0); B(0 | 0 | 0); C(−4 | 0 | 0); D(−4 | −5 | 0); E(0 | −5 | 3);
F(0 | 0 | 3); G(−4 | 0 | 3); H(−4 | −5 | 3)
JJJG ⎛⎜ −4 ⎞⎟ JJJG ⎛⎜ 4 ⎞⎟ JJJG ⎛⎜ 4 ⎞⎟
EG = 5 ; CA = −5 ; HB = 5
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝0 ⎠
⎝0⎠
⎝ −3 ⎠
JJJG ⎛⎜ 4 ⎞⎟ JJJG ⎛⎜ 4 ⎞⎟
13. a) AB = −6 ; DC = −6
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ −4 ⎠
⎝ −4 ⎠
Die Seiten AB und CD sind parallel und gleich lang.
ABCD ist ein Parallelogramm.
168
227
JJJG ⎛ −4 ⎞ JJJG ⎛ −12 ⎞
13. b) AB = ⎜ 5 ⎟ ; CD = ⎜ 11 ⎟ ⇒ AB & CD;
⎜⎜ ⎟⎟
⎜⎜
⎟⎟
⎝ 2⎠
⎝ 6 ⎠
JJJG ⎛ 4 ⎞ JJJG ⎛ −4 ⎞
AC = ⎜ −3 ⎟ ; BD = ⎜ 3 ⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ −2 ⎠
⎝ 2⎠
Die Seiten AC und BD sind parallel und gleich lang.
ACBD ist ein Parallelogramm.
14.
15. a) D (−2 | 3 | 2)
JJJG JJJG
b) Kein Parallelogramm möglich, da AB = BC .
JJJG JJJG
c) Kein Parallelogramm möglich, da AC = CB .
JJJG JJJG
d) Kein Parallelogramm möglich, da BC = CA .
16. Da die Basis des gleichschenkligen Dreiecks nicht vorgegeben ist, gibt es
mehrere Lösungsmöglichkeiten:
JJJG
JJJG
a) Basis AB ⇒ AC = BC ⇒ t = 13
4
JJJG
JJJG
Basis BC ⇒ AB = AC ⇒ t = −3 oder t = −1
JJJG
JJJG
Basis AC ⇒ AB = BC keine Lösung
JJJG
JJJG
b) Basis AB ⇒ AC = BC keine Lösung
JJJG
JJJG
Basis BC ⇒ AB = AC keine Lösung
JJJG
JJJG
Basis AC ⇒ AB = BC ⇒ t = 8 oder t = 6
169
227
⎛− 2 ⎞
⎛ 2⎞
⎛0 ⎞
⎜ 3⎟
JJJG
JJJG
JJJG
17. a) AB = ⎜ 0 ⎟ = 8; AC = ⎜ 2 ⎟ = 8; AD = ⎜ − 23 ⎟ = 8
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜ ⎟
⎝ −2 ⎠
⎝ −2 ⎠
⎜−8⎟
⎝ 3⎠
⎛−8⎞
⎛− 2 ⎞
⎛ −2 ⎞
⎜ 3⎟
⎜ 3⎟
JJJG
JJJG
JJJ
G
BC = ⎜ 2 ⎟ = 8; BD = ⎜ − 23 ⎟ = 8; CD = ⎜ − 83 ⎟ = 8
⎜⎜ ⎟⎟
⎜ ⎟
⎜ ⎟
⎝0 ⎠
⎜− 2 ⎟
⎜− 2 ⎟
⎝ 3⎠
⎝ 3⎠
Alle Kanten haben die Länge
b) Oberfläche des Tetraeders:
8 ≈ 2,83.
3 ⋅ ( 8 ) = 8 3 ≈ 13,86
2
JJJG JJJG JJJG JJG JJJG JJJG JJG JJJG
18. a) PR = PQ + QR = RS + QR = QR + RS = QS
JJJG JJG
b) Gilt PQ = RS , dann ist das Viereck PQSR ein Parallelogramm.
JJJG ⎛ −2 ⎞ JJJG ⎛ 2 ⎞
19. a) AB = ⎜ 6 ⎟ ; CD = ⎜ −6 ⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ 3⎠
⎝ −3 ⎠
AB ist parallel zu CD und gleich lang.
ABCD bildet ein Parallelogramm.
Seitenlängen:
JJJG
JJJG
AB = CD = 49 = 7
⎛ −6 ⎞
JJJG
BC = ⎜ −3 ⎟ =
⎜⎜ ⎟⎟
⎝ 2⎠
JJJG
49 = 7 = AD
Alle Seiten sind 7 Einheiten lang.
JJJG 2 JJJG 2
JJJG 2
b) Z. B.: Über den Satz des Pythagoras: Wenn AB + BC = AC gilt,
dann steht die Seite AB senkrecht auf BC und demnach sind alle
Winkel im Parallelogramm rechte Winkel.
⎛ −8 ⎞
JJJG
JJJG 2
Hier:
AC = ⎜ 3 ⎟ = 98
AC = 98
⎜⎜ ⎟⎟
⎝ 5⎠
JJJG 2 JJJG 2
AB + BC = 98
Es ist ein Rechteck.
170
4.1.4 Vervielfachen von Vektoren
230
Information (5)
Aus der Skizze klar:
JJJJG JJJG
JJJG
OM = OA + 12 AB
JJJJG
JJJG
JJJG
⇔ OM = 12 ( OA ⋅ 2 + AB)
JJJJG
JJJG JJJG JJJG
⇔ OM = 12 ( OA + OA + AB)
JJJG JJJG JJJG
JJJJG
JJJG JJJG
und da OA + AB = OB: ⇔ OM = 12 ( OA + OB)
⎛ 1, 5 ⎞
2. a) Nach 1 Stunde: ⎜ 2 ⎟
⎜ 0, 5 ⎟
⎝
⎠
⎛ 1, 5 ⎞ ⎛ 3 ⎞
Nach 2 Stunden: 2 ⋅ ⎜ 2 ⎟ = ⎜ 4 ⎟
⎜ 0, 5 ⎟ ⎜ 1 ⎟
⎝
⎠ ⎝ ⎠
3 m tief, 4 m nördlich, 1 m westlich.
⎛ 1, 5 ⎞ ⎛ 4, 5 ⎞
Nach 3 Stunden: 3 ⋅ ⎜ 2 ⎟ = ⎜ 6 ⎟
⎜ 0, 5 ⎟ ⎜ 1, 5 ⎟
⎝
⎠ ⎝
⎠
4,5 m tief, 6 m nördlich, 1,5 m westlich.
⎛ 1, 5 ⎞ ⎛ 6 ⎞
Nach 5 Stunden: 5 ⋅ ⎜ 2 ⎟ = ⎜ 10 ⎟
⎜ 0, 5 ⎟ ⎜ 2, 5 ⎟
⎝
⎠ ⎝
⎠
6 m tief, 10 m nördlich, 2,5 m westlich.
b)
⎛ −2 ⎞
3. a) ⎜ 10 ⎟
⎜ 14 ⎟
⎝ ⎠
⎛ 3 ⎞
b) ⎜ −6 ⎟
⎜ 4, 5 ⎟
⎝
⎠
⎛ −2 ⎞
c) ⎜ 0 ⎟
⎜ −2, 5 ⎟
⎝
⎠
⎛ −6 ⎞
d) ⎜ −3 ⎟
⎜ 15 ⎟
⎝ ⎠
⎛ 5 ⎞
e) ⎜ −7, 5 ⎟
⎜ 6, 25 ⎟
⎝
⎠
171
230
4. (1) Wegen der ersten Koordinate müsste der Faktor (−1) sein.
Dies passt nicht zur dritten Koordinate.
(2) Wegen der ersten Koordinate müsste der Faktor
1
2
sein.
Dies passt weder zur zweiten noch zur dritten Koordinate.
(3) Wegen der ersten Koordinate müsste der Faktor
1
2
sein.
Dies passt nicht zur dritten Koordinate.
G
G
(4) Da a und b die gleiche x 3 -Koordinate haben aber unterschiedliche
G
G
x1 - und x 2 -Koordinaten kann b kein Vielfaches von a sein.
5. Mehrere Lösungen immer möglich; einfache Beispiele:
⎛ 4⎞
G
a) a = 16 ⋅ ⎜ −6 ⎟
⎜⎜ ⎟⎟
⎝ 3⎠
⎛ −48 ⎞
G 1 ⎜
b) a = 12
⋅ −9 ⎟
⎜⎜
⎟⎟
⎝ 4 ⎠
⎛3⎞
G
c) a = 6 ⋅ ⎜ 2 ⎟ Hier wäre die Aufgabenstellung ebenfalls eine Lösung.
⎜⎜ ⎟⎟
⎝4⎠
⎛ −3 ⎞
G
d) a = 16 ⋅ ⎜ 120 ⎟
⎜⎜
⎟⎟
⎝ 4 ⎠
G
G
G G
6. (1) 1 a + 1 b
(2) − a + b
2
2
G
G
(3) a + 1 b
2
G
(4) 1 b
2
JJJG ⎛ −6 ⎞ JJJG ⎛ 4 ⎞ JJJG ⎛ 10 ⎞
7. AB = ⎜ 4 ⎟ ; AC = ⎜ −6 ⎟ ; BC = ⎜ −10 ⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜
⎟⎟
⎝ 2⎠
⎝ −2 ⎠
⎝ −4 ⎠
⎛ −3 ⎞
JJJJJJJG
JJJG JJJG
M a M b = 12 ( AC − BC ) = ⎜ 2 ⎟
⎜⎜ ⎟⎟
⎝1⎠
⎛ −2 ⎞
JJJJJJJG
JJJG JJJG
M a M c = 12 ( − BC − AB) = ⎜ 3 ⎟
⎜⎜ ⎟⎟
⎝ 1 ⎠
⎛ −5 ⎞
JJJJJJJG
JJJG JJJG
M b M c = 12 ( −AC + AB) = ⎜ 5 ⎟
⎜⎜ ⎟⎟
⎝2⎠
Die Dreiecke ABC und M a M b M c sind gleichschenklig und zudem
ähnlich.
172
231
8.
9. M(2 | 3 | 5) ist nicht der Mittelpunkt von AB , sondern die Hälfte des
JJJG ⎛ 2 ⎞ ⎛ 2 ⎞ ⎛ 4 ⎞
JJJG
G JJJG
Vektors AB . Der Mittelpunkt ist m = OA + 12 AB = ⎜ 8 ⎟ + ⎜ −3 ⎟ = ⎜ 5 ⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝ −4 ⎠ ⎝ 5 ⎠ ⎝ 1 ⎠
⇒ M(4 | 5 | 1).
JJJG G G
G JJJG JJJJG JJJG
10. a)/b) m = OA + AM = OA + 12 AB = a + p
JJJJJG G
G
G
11. AM1 = a + 12 b + 12 c
JJJJJG
G
G
HM 3 = − 12 c − 12 b
JJJG
G G
G
12. MS = − 12 ( a + b ) + c
⎛ 2 ⎞
3
G ⎜ ⎟
13. a) a = ⎜ − 13 ⎟
⎜ ⎟
⎜ 2 ⎟
⎝ 3 ⎠
JJJG
G
14. PQ = 12 b +
G
1a
2
JJJJJJJG
G
M1M 2 = 12 b −
JJJJJG
G
M 2 A = − 12 c −
JJJG
G G
G
CS = − ( a + b ) + c
G
1a
2
G
1a
2
JJG G G
SB = a − c
⎛ 5⎞
⎛9⎞
G
G
b) a = 1 ⎜ 3 ⎟ c) a = 1 ⎜ 0 ⎟
⎟⎟
5 2 ⎜⎜
106 ⎜⎜ ⎟⎟
⎝ −4 ⎠
⎝ 5⎠
G
G G
G
− c = 12 ( a + b ) − c
G
−b
⎛1⎞
G
d) a = 1 ⎜ 0 ⎟
2 ⎜⎜ ⎟⎟
⎝1⎠
173
Blickpunkt: Bewegung auf dem Wasser
232
1. a)
v1
v1
65
v2
v2
v2
v
127
v
G
α = 65°: v ≈ 6,9 m
G
α = 127°: v = 4 m
s
s
Kontrollrechnung mit Kosinussatz:
JJG 2 JJG 2
JJG JJG
G2
v = v1 + v 2 − 2 v1 v 2 cos(180° − α )
G
⇒ α = 65° ⇒ v = 6,83 m
s
G
α = 127° ⇒ v = 3,9932 m
s
G JJG JJG ⎛ 2 ⎞
b) v = v1 + v 2 = ⎜ ⎟
⎝ 4⎠
G
v = 20 m ≈ 4, 47 m
s
s
2. Nach Kosinussatz: 35 405,8 N
233
G
G
3. a) Sei α der Winkel, den die Vektoren FSchlepper und v, also die Kraft
des Schleppers und Bewegungsrichtung, bilden.
G
Dann gilt für die wirksame Kraft entlang v :
G
G
F wirksam = FSchlepper ⋅ cos α
G
Im Bild ist α = 45° ⇒ F wirksam ≈ 24 748,7 N
b)
zeichnerisch:
F⊥ ≈ 49 218,8 N
Fhinab ≈ 8 593,8 N
rechnerisch:
F⊥ = 50 000 N ⋅ cos (9°) = 49 384,4 N
Fhinab = 50 000 N ⋅ sin (9°) ≈ 7 821,7 N
v2
174
233
3. b) Fortsetzung
allgemein:
F⊥ = 50 000 N ⋅ cos (α)
Fhinab = 50 000 N ⋅ sin (α)
=0N
⎧F
Extremfälle für α = 0 ⇒ ⎨ hinab
=
F
50
000 N
⎩ ⊥
= 50 000 N
⎧F
α = 90° ⇒ ⎨ hinab
=
F
0
N
⎩ ⊥
Bis α = 45° gilt F⊥ > Fhinab danach F⊥ < Fhinab .
4.
4.2 Geraden im Raum
4.2.1 Parameterdarstellung einer Geraden
236
2. a) Z. B.:
JJJG ⎛ 3 ⎞ ⎛ −5 ⎞
JJJG ⎛ −2 ⎞ ⎛ 5 ⎞
g: OX = ⎜ 1 ⎟ + t ⎜ 3 ⎟ ; t ∈ \ , g: OX = ⎜ 4 ⎟ + t ⎜ −3 ⎟ ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝ −2 ⎠ ⎝ −5 ⎠
⎝ −7 ⎠ ⎝ 5 ⎠
175
236
2. b) Weitere Darstellungen erhält man entweder durch das Ändern des
Stützvektors zu einem Ortsvektor eines anderen Punktes auf der Geraden
oder durch Vervielfachen des Richtungsvektors oder beides gleichzeitig:
JJJG ⎛⎜ 8 ⎞⎟ ⎛⎜ 10 ⎞⎟
Beispiel: g: OX = −2 + t −6 ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝ 3 ⎠ ⎝ 10 ⎠
⎛ 3⎞ ⎛ 5⎞
G ⎜ ⎟ ⎜ ⎟
g: x = 1 + t −3 ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝ −2 ⎠ ⎝ 5 ⎠
⎛ −2 ⎞ ⎛ −2, 5 ⎞
G ⎜ ⎟ ⎜
g: x = 4 + t 1, 5 ⎟ ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜
⎟⎟
⎝ −7 ⎠ ⎝ −2, 5 ⎠
⎛ −7 ⎞ ⎛ −20 ⎞
G ⎜
g: x = 7 ⎟ + t ⎜ 12 ⎟ ; t ∈ \
⎜⎜
⎟⎟ ⎜⎜
⎟⎟
⎝ −12 ⎠ ⎝ −20 ⎠
JJJG ⎛ 4 ⎞
3. Zunächst wird der Punkt A aus dem Stützvektor OA = ⎜ 3 ⎟ eingezeichnet.
⎜ 3⎟
⎝ ⎠
2
−
⎛ ⎞
Von Punkt A ausgehend wird der Richtungsvektor ⎜ 1 ⎟ eingezeichnet
⎜ −3 ⎟
⎝ ⎠
und dieser in beide Richtungen zu einer Geraden verlängert.
176
236
4. a) S12 (3 | 4 | 0); S13 (1 | 0 | 2); S23 (0 | −2 | 3)
Zeichnung: siehe Aufgabenstellung.
Die Gerade verläuft vor der x 3 -Achse bis sie den Spurpunkt S23
erreicht.
b) S12 (−6 | 2 | 0); S13 (−2 | 0 | 6); S23 (0 | −1 | 9)
Die Gerade verläuft hinter der x 3 -Achse im Großteil der Zeichnung,
erst bei S23 kommt sie nach vorne.
237
5. a) Nach 1 Minute:
A1 (5308 | 870 | −38)
A 3 (5456 | 1000 | −46)
A 5 (5604 | 1130 | −54)
Nach 5 Minuten:
Die Punkte liegen auf einer Geraden.
Nach 3 Minuten:
JJJG ⎛⎜ 5234 ⎞⎟ ⎛⎜ 74 ⎞⎟
b) OX = 805 + t 65 mit t ∈ \, t gemessen in Minuten.
⎜⎜
⎟⎟ ⎜⎜ ⎟⎟
⎝ −34 ⎠ ⎝ −4 ⎠
Der Ortsvektor ist gegeben durch den Ortsvektor des Startpunktes und
ein Vielfaches des Vektors der Bewegungsrichtung.
c) Nach 13 Minuten erreicht das Tauchboot den Punkt Q.
177
237
6. Es gibt unendlich viele Lösungen. Beispiele:
⎛0⎞
⎛ 3⎞
⎛ 3⎞
G ⎜ ⎟
⎜
⎟
g: x = 0 + s −2 = s ⎜ −2 ⎟ ; s ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝0⎠
⎝ 4⎠
⎝ 4⎠
⎛ 3⎞
⎛ 3⎞
G ⎜ ⎟
g: x = −2 + r ⎜ −2 ⎟ ; r ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ 4⎠
⎝ 4⎠
⎛ −3 ⎞ ⎛ 6 ⎞
G ⎜ ⎟ ⎜ ⎟
g: x = 2 + t −4 ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝ −4 ⎠ ⎝ 8 ⎠
⎛ −2 ⎞ ⎛ 4 ⎞
G ⎜ ⎟ ⎜ ⎟
7. a) Z. B.: g: x = 5 + t −8 ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝ 3 ⎠ ⎝ −2 ⎠
⎛2⎞
⎛ −4 ⎞
G ⎜ ⎟
oder g: x = −3 + s ⎜ 8 ⎟ ; s ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝1⎠
⎝ 2⎠
P liegt auf g (im Beispiel: t = −3, s = 4)
⎛ 5 ⎞ ⎛ −3 ⎞
G
b) Z. B.: g: x = ⎜ −3 ⎟ + t ⎜ 2 ⎟ ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝ −1 ⎠ ⎝ 3 ⎠
⎛2⎞
⎛ −6 ⎞
G
oder g: x = ⎜ −1 ⎟ + s ⎜ 4 ⎟ ; s ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝2⎠
⎝ 6⎠
P liegt nicht auf g.
178
237
⎛ −3 ⎞
⎛3⎞
G ⎜ ⎟
8. a) (3) g: x = −3 + r ⎜ 2 ⎟ ; r ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝1⎠
⎝ −1 ⎠
(
|0
b) (1) 2, 5 | 17
4
)
(2) (0 | 1 | 0)
(3) (0 | −1 | 0)
Dies sind jeweils die Schnittpunkte der Geraden g mit der x1x 2 -Ebene .
9. a) Ursprungsgerade in x1x 2 -Ebene
b) x 2 -Achse
c) Ursprungsgerade in x 2 x 3 -Ebene
d) Gerade verläuft in x 2 x 3 -Ebene
⎛1⎞ ⎛1⎞
G
z. B.: g: x = ⎜ 1 ⎟ + t ⎜ 1 ⎟ ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝0⎠ ⎝0⎠
⎛0⎞ ⎛0⎞
G
z. B.: x = ⎜ 1 ⎟ + t ⎜ 1 ⎟ ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝0⎠ ⎝0⎠
⎛0⎞ ⎛0⎞
G
z. B.: g: x = ⎜ 1 ⎟ + t ⎜ 1 ⎟ ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝ −1 ⎠ ⎝ −1 ⎠
⎛2⎞ ⎛1⎞
G
z. B.: g: x = ⎜ 0 ⎟ + t ⎜ 0 ⎟ ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝3⎠ ⎝1⎠
179
237
⎛ −5 ⎞ ⎛ 4 ⎞
G ⎜ ⎟ ⎜ ⎟
10. a) Z. B: g: x = 3 + t 2
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝ 1 ⎠ ⎝ −8 ⎠
b) Die Richtungsvektoren sind Vielfache voneinander:
⎛ 2 ⎞ ⎛ −10 ⎞
− 5 ⋅ ⎜ 1 ⎟ = ⎜ −5 ⎟ .
⎜⎜ ⎟⎟ ⎜⎜
⎟⎟
⎝ −4 ⎠ ⎝ 20 ⎠
⎛ 29 ⎞
Der Stützvektor ⎜ 20 ⎟ liegt auf g (für k = 17). Es ist die selbe Gerade.
⎜⎜
⎟⎟
⎝ −67 ⎠
11. a) Alle Punkte der Strecke AB mit A(−4 | −6 | 3) und B(1 | 9 | 3)
inklusive der Punkte A und B.
b) Alle inneren Punkte der Strecke CD mit C(4 | 0 | −4) und D(20 | −8 | 0)
(d. h. exklusive der Punkte C und D).
12. a) (1) (0 | 11 | −1)
238
(2) (8 | 3 | −5) b) (1) (0 | 15 | 0) (2) (−18 | 3 | 12)
13. a) A liegt auf g für k = −2.
B liegt nicht auf g.
C liegt auf g für k = 5.
b) A liegt auf g für t = −3.
B liegt nicht auf g.
C liegt nicht auf g.
JJJG ⎛ −2 ⎞
JJJG ⎛⎜ 3 ⎞⎟
14. a) PQ = ⎜ −4 ⎟ ,
PR = 6
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ 4⎠
⎝ −6 ⎠
JJJG
JJJG
3
Da PR = − 2 ⋅ PQ liegen P, Q, R auf einer Geraden und da der Vorfaktor negativ ist, liegt P zwischen Q und R.
JJJG ⎛⎜ 24 ⎞⎟
JJJG ⎛⎜ 15 ⎞⎟
JJJG
JJJG
b) PQ = −32 ,
PR = −20 , PR = 85 PQ
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎝ 16 ⎠
⎝ 10 ⎠
P, Q, R liegen auf einer Geraden. Da 85 < 1 liegt Q näher an P als R.
Q liegt in der Mitte.
15. Beim Stützvektor kommt es auf die Länge an. Nur beim Richtungsvektor ist die Länge irrelevant. Zu einem bekannten Stützvektor dürfen
Vielfache eines Richtungsvektors addiert werden. Kristins alternative
Darstellung der Geraden ist daher falsch.
180
238
16. a) P(−4634 | 2035 | −500)
JJJJG ⎛⎜ 69 ⎞⎟
b) PW = 80
⎜⎜ ⎟⎟
⎝ −8 ⎠
JJJJG
Entfernung Tauchboot zum Wrack ist die Länge des Vektors PW :
JJJJG
PW = 11 225 ≈ 105, 95 > 100
Die Crew sieht das Wrack nicht.
⎛ 11 ⎞
⎛ −6 ⎞
G ⎜ ⎟
17. a) Z. B. g: x = 1 + k ⎜ −2 ⎟ ; k ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝6⎠
⎝ −4 ⎠
Für 0 < k < 1 liegen alle Punkte der Geraden zwischen A und B,
z. B. k = 12 → (8 | 0 | 4) oder k = 14 → (9,5 | 0,5 | 5)
b) Für k = 25 ergibt sich der Ortsvektor vom Punkt (−4 | −4 | −4).
⎛4⎞
⎛1 ⎞
G ⎜ ⎟
18. a) Z. B.: g′: x = −3 + k ⎜ 1 ⎟ ; k ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝2⎠
⎝ −2 ⎠
⎛ −5 ⎞
⎛0⎞
G ⎜ ⎟
b) Z. B.: g′: x = −2 + r ⎜ −1 ⎟ ; r ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ −2 ⎠
⎝ −1 ⎠
⎛ 2⎞
⎛ −2 ⎞
G ⎜ ⎟
c) Z. B.: g′: x = −2 + k ⎜ 0 ⎟ ; k ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝1 ⎠
⎝ 3⎠
19. Es gibt unendlich viele äquivalente Lösungen. Als Beispiel wird der
Ursprung des Koordinatensystems immer in die untere, hintere, linke Ecke
des Körpers gelegt und das Standard-Rechtssystem verwendet. Alle Einheiten sind cm.
⎛4⎞
⎛ −4 ⎞
⎛2⎞
⎛0⎞
G
G
a) g: x = ⎜ 0 ⎟ + k ⋅ ⎜ 6 ⎟ ; k ∈ \
h: x = ⎜ 0 ⎟ + r ⋅ ⎜ 6 ⎟ ; r ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝0⎠
⎝ 3⎠
⎝3⎠
⎝ −3 ⎠
⎛0⎞
⎛2⎞
G
i: x = ⎜ 3 ⎟ + t ⋅ ⎜ 3 ⎟ ; t ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝3⎠
⎝ −3 ⎠
⎛0⎞
⎛4⎞
G
k: x = ⎜ 3 ⎟ + s ⋅ ⎜ 3 ⎟ ; s ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝3⎠
⎝ −3 ⎠
181
238
⎛4⎞
⎛ −4 ⎞
G ⎜ ⎟
19. b) g: x = 6 + k ⋅ ⎜ −3 ⎟ ; k ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝0⎠
⎝ 3⎠
⎛2⎞
⎛ −2 ⎞
G ⎜ ⎟
i: x = 6 + t ⋅ ⎜ −6 ⎟ ; t ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝0⎠
⎝ 3⎠
⎛0⎞
⎛ 3 ⎞
G ⎜ ⎟
c) g: x = 0 + t ⋅ ⎜ 3 ⎟ ; t ∈ \
⎜⎜ ⎟⎟
⎜⎜
⎟⎟
⎝0⎠
⎝ 2, 5 ⎠
⎛0⎞
⎛2⎞
G ⎜ ⎟
h: x = 3 + r ⋅ ⎜ 3 ⎟ ; r ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝3⎠
⎝ −3 ⎠
⎛2⎞
⎛ −2 ⎞
G ⎜ ⎟
k: x = 0 + s ⋅ ⎜ 6 ⎟ ; s ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝0⎠
⎝ 3⎠
⎛4⎞
⎛ −2 ⎞
G ⎜ ⎟
i: x = 0 + s ⋅ ⎜ 4 ⎟ ; s ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝0⎠
⎝0⎠
⎛2⎞
⎛2⎞
G ⎜ ⎟
k: x = 4 + r ⋅ ⎜ 2 ⎟ ; r ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝0⎠
⎝ 5⎠
239
⎛2⎞
JJJG ⎛ 1 ⎞
20. OX = ⎜ 0 ⎟ + t ⋅ ⎜ −1⎟
⎜ 3⎟
⎜4⎟
⎝ ⎠
⎝ ⎠
JJJJG ⎛⎜ 3 + 2t ⎞⎟ ⎛⎜ 3 ⎞⎟ ⎛⎜ 2 ⎞⎟
21. a) OPt =
5t
= 0 +t 5 ; t∈\
⎜⎜
⎟⎟ ⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
2
4t
−
−
⎝
⎠ ⎝ −2 ⎠ ⎝ −4 ⎠
Dies ist die Parameterdarstellung einer Geraden.
Alle Punkte Pt liegen auf dieser Geraden.
JJJJJJG ⎛ 2 ⎞
JJJJJJG ⎛ 4 ⎞
b) A1A 2 = ⎜ −2 ⎟ ,
A 1 A 3 = ⎜ −4 ⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ 3⎠
⎝ 8⎠
JJJJJJG
JJJJJJG
⇒ A1A 2 ist kein Vielfaches von A1A 3 , somit liegen A1 , A 2 , A 3
nicht auf einer Geraden. Daher liegen nicht alle A t auf einer Geraden.
⎛ −2080 ⎞
JJJJJG
22. a) k 0 k 1 = ⎜ 720 ⎟ =
⎜⎜
⎟⎟
⎝ −320 ⎠
4 947 200 ≈ 2224, 23 m
Die Zeit zwischen k 0 und k 1 beträgt 32 s.
Geschwindigkeit: v =
JJJJJG
k 0 k1
32 s
= 69, 51
m
s
.
182
239
22. b) Flugbahn als Gerade:
JJJJJJG
G JJJJJG
g: x = OK 0 + r ⋅ K 0 K1 ; r ∈ \
Für r = 3,1875 wird x 3 = 0 (Landung).
Dies erfolgt im Punkt (1415 | 40 | 0).
Eine Kurskorrektur ist notwendig.
Neue Gerade der Flugbewegung:
JJJJG
G JJJJJG
h: x = OK1 + t ⋅ K1 L; t ∈ \ , d. h. der neue Kurs ab K1 ist
JJJJG ⎛⎜ −4465 ⎞⎟
K1 L = 1585 .
⎜⎜
⎟⎟
⎝ −700 ⎠
23. a) S12 (2 | −1 | 0)
S13
( 43 | 0 | 1)
S 23 (0 | 2 | 3)
Von links unten kommend,
schneidet die Gerade im
Punkt S12 die x1x 2 -Ebene
und verläuft vor der
x 2 -Achse bis zum
Schnittpunkt S13 mit der
x1x 3 -Ebene. Weiter
verläuft sie vor der
x 3 -Achse bis zum
Schnittpunkt S 23 mit
der x 2 x 3 -Ebene und bleibt dann im oberen, hinteren Oktanden.
b) S12 (10 | 2 | 0)
S13 (10 | 0 | 3)
S 23 existiert nicht
Die Gerade verläuft
parallel zur x 2 x 3 -Ebene.
Von oben links
kommend, passiert sie
S13 und verläuft vor der
x1 -Achse bis S12 .
Nach S12 bleibt sie im
vorderen, unteren, rechten
Oktanden.
183
239
23. c) S12 existiert nicht
S13 existiert nicht
S 23 (0 | −2 | 4)
Die Gerade ist parallel
zur x1 -Achse. Von
unten links kommend,
verläuft sie im oberen,
vorderen, linken
Oktanden, bis sie bei
S 23 die x 2 x 3 -Ebene
durchstößt und hinter der
x 3 -Achse im hinteren,
oberen, linken Oktanden
bleibt.
24. a) S12 (6 | 0 | 0)
S13 (6 | 0 | 0)
S 23 (0 | 2 | 5)
Die Gerade
schneidet die
x1 -Achse im
Punkt S12 = S13 .
b) S12 (0 | 0 | 0)
S13 (0 | 0 | 0)
S 23 (0 | 0 | 0)
Es ist eine Ursprungsgerade, alle 3 Spurpunkte fallen im
Ursprung
zusammen.
184
239
24. c) S12 (0 | 8 | 0)
S13 (−16 | 0 | −24)
S 23 (0 | 8 | 0)
Die Gerade schneidet die
x 2 -Achse im Punkt S12 = S 23 .
Sie hat nur 2 Spurpunkte.
240
25. a) Die Gerade ist parallel zu der x1x 3 -Ebene .
⎛1⎞
⎛1⎞
G
Z. B. g: x = ⎜ 2 ⎟ + s ⎜ 0 ⎟ ; s ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝3⎠
⎝1⎠
⎛0⎞
⎛1⎞
G
b) Bei Ursprungsgeraden. Z. B. g: x = ⎜ 0 ⎟ + s ⎜ 1 ⎟ ; s ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝0⎠
⎝1⎠
⎛1⎞ ⎛1⎞
G
c) Z. B. g: x = ⎜ 2 ⎟ + t ⎜ 2 ⎟ ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝3⎠ ⎝0⎠
⎛1⎞ ⎛1⎞
G
z. B. g: x = ⎜ 2 ⎟ + t ⎜ 0 ⎟ ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝3⎠ ⎝0⎠
185
240
⎛1⎞ ⎛1⎞
G ⎜ ⎟ ⎜ ⎟
25. d) Z. B. g: x = 0 + t 2 ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝0⎠ ⎝3⎠
⎛0⎞ ⎛4⎞
G ⎜ ⎟ ⎜ ⎟
z. B. g: x = 1 + t 2 ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝0⎠ ⎝1⎠
26. S12 (4 | 3 | 0)
S13 (−8 | 0 | 6)
S 23 (0 | 2 | 2)
⎛1⎞
⎛ −4 ⎞
G ⎜3⎟
27. a) S13 (4 | 0 | 3); S 23 (0 | 2 | 3); z. B. g: x = ⎜ 2 ⎟ + s ⎜ 2 ⎟ ; s ∈ \
⎜⎜ ⎟⎟
⎜3⎟
⎝0 ⎠
⎝ ⎠
⎛2⎞ ⎛0⎞
G ⎜ ⎟ ⎜ ⎟
b) S13 (2 | 0 | 3); z. B. g: x = 4 + t 1 ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝3⎠ ⎝0⎠
186
240
28. g1 : parallel zur x 3 -Achse und in der x 2 x 3 -Ebene
g 2 : in der x1x 3 -Ebene
g 3 : Ursprungsgerade in der x1x 3 -Ebene
g 4 : keine besondere Lage
29.
Nach dem Verfahren von Aufgabe 3 landet man bei der Konstruktion des
Stützvektors und des Richtungsvektors auf derselben Stelle in der Zeichnung, die Punkte sind aber unterschiedlich. Der Richtungsvektor kommt
dem Betrachter entgegen, sodass man ihn in dieser Zeichnung „nicht sieht“.
Weitere Beispiele:
⎛ 5⎞ ⎛2⎞
G
g: x = ⎜ 0 ⎟ + t ⎜ 1 ⎟ ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝0⎠ ⎝1⎠
⎛ 2⎞
und alle Geraden mit Richtungsvektoren, die Vielfache von ⎜ 1 ⎟ sind.
⎜1⎟
⎝ ⎠
187
240
⎛0⎞
⎛0⎞
G ⎜ ⎟
30. a) Z. B. g1 : x = 0 + k ⎜ 1 ⎟ ; k ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝4⎠
⎝0⎠
G
Allgemein: Für den Stützvektor v muss gelten:
⎛1⎞
⎛0⎞
G
G
v = a ⋅ ⎜ 0 ⎟ + b ⎜ 0 ⎟ mit v = 4 und a, b ∈ \ .
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝0⎠
⎝1⎠
⎛0⎞
Der Richtungsvektor muss ein Vielfaches von ⎜ 1 ⎟ sein.
⎜⎜ ⎟⎟
⎝0⎠
⎛0⎞
⎛1⎞
G
b) Z. B. g: x = ⎜ 0 ⎟ + k ⎜ 1 ⎟ ; k ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝2⎠
⎝0⎠
G G
G
Allgemein: g: x = v + k ⋅ w; k ∈ \
⎛0⎞
⎛ −1 ⎞
G
G
mit v = a ⋅ ⎜ 0 ⎟ + b ⎜ 1 ⎟ und v = 2 und a, b ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝1⎠
⎝0⎠
⎛1⎞
G
und w = c ⋅ ⎜ 1 ⎟ mit c ∈ \ \ {0} .
⎜⎜ ⎟⎟
⎝0⎠
c) Mögliches Vorgehen:
⎛1⎞
G
G
- Richtungsvektor w parallel zur x1 -Achse ⇒ w Vielfaches von ⎜ 0 ⎟
⎜⎜ ⎟⎟
⎝0⎠
⎛ v1 ⎞
G
- Stützvektor v = ⎜ v 2 ⎟ muss in x1x 3 -Ebene liegen ⇒ v 2 = 0
⎜ ⎟
⎜v ⎟
⎝ 3⎠
Der Abstand von der x1 -Achse muss 3 betragen ⇒ v 3 = 3
v1 bleibt beliebig.
⎛ v1 ⎞
⎛1⎞
G
⇒ g: x = ⎜ 0 ⎟ + t ⋅ ⎜ 0 ⎟ ; t ∈ \, v1 ∈ \ beliebig aber fest.
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝3⎠
⎝0⎠
⎛ −1 ⎞
JJJG ⎛ 1 ⎞
31. OX = ⎜ −2 ⎟ + t ⋅ ⎜ 1 ⎟ ; R(2 | r2 | r3 )
⎜1 ⎟
⎜3⎟
⎝ ⎠
⎝ ⎠
Punktprobe für R bringt für die 1. Koordinate x1 :
2 = 1 − t; t = −1 also R(2 | −3 | −2)
188
4.2.2 Lagebeziehungen zwischen Geraden
243
3. (1) Die Richtungsvektoren sind keine Vielfachen voneinander.
3r − 2t = −1
Das lineare Gleichungssystem − r + t = 1
4r − t = 2
hat keine Lösung, d. h. g und h sind zueinander windschief.
(2) Die Richtungsvektoren sind Vielfache voneinander, da
⎛ 1,5 ⎞ ⎛ 3 ⎞
2 ⋅ ⎜ −0,5 ⎟ = ⎜ −1⎟ . Da aber (5 | 7 | 5) nicht auf g liegt, sind die
⎜ 2 ⎟ ⎜4⎟
⎝
⎠ ⎝ ⎠
Geraden g und k parallel.
(3) Die Richtungsvektoren sind keine Vielfachen voneinander.
3r − 2t = 3
Das lineare Gleichungssystem − r − t = −1
4r + 8t = −1
hat keine Lösung, d. h. g und l sind zueinander windschief.
4. a)
b)
c)
d)
g und h schneiden sich im Punkt S(−5 | 1 | 4).
g und h sind zueinander parallel.
g und h sind identisch.
g und h sind windschief.
5. g & h, die Richtungsvektoren sind nicht kollinear zueinander.
⎛2⎞
⎛ −1 ⎞ ⎛ 4 ⎞
⎛ 3⎞
⎜ 0 ⎟ + r ⎜ 2 ⎟ = ⎜ 4⎟ + s⎜ 2 ⎟
⎜3⎟
⎜ 2 ⎟ ⎜0⎟
⎜ −5 ⎟
⎝ ⎠
⎝ ⎠ ⎝ ⎠
⎝ ⎠
− r − 3s = 6
2r − 2s = 4 ; 3. Gleichung von 2. Gleichung subtrahieren ergibt:
2r + 5s = 0
r = − 30
7
− r − 3s = 6 r = −3s − 6
2r − 2s = 4 ; r = s + 2 ; r = 10
7
− 7s = 4 s = − 4
s = −4
7
7
Es entsteht ein Widerspruch; g und h sind zueinander windschief.
189
243
5. Fortsetzung
g & k, die Richtungsvektoren sind nicht kollinear zueinander.
⎛2⎞
⎛ −1 ⎞ ⎛ 2, 5 ⎞ ⎛ −3 ⎞
⎜ 0 ⎟ + r ⎜ 2 ⎟ = ⎜ 4 ⎟ + t ⎜ −2 ⎟
⎜3⎟
⎜2⎟ ⎜ 0 ⎟ ⎜ 5⎟
⎝ ⎠
⎝ ⎠ ⎝
⎠ ⎝ ⎠
− r + 3t = 0, 5
2r + 2t = 4 ; 3. Gleichung von 2. Gleichung subtrahieren ergibt:
2r − 5t = −3
− r + 3t = 0, 5 r = 3t − 0, 5
r = 2, 5
2r + 2t = 4 r = − t + 2 ; r = 1 ; Widerspruch
7t = 7 t = 1
t =1
Die Geraden g und k sind zueinander windschief.
h & k, die Richtungsvektoren sind kollinear zueinander.
Punktprobe für (2,5 | 4 | 0) bei h:
r = −1
2, 5 = 2 − r
2
4 = 0 + 2r ; r = 2 ; h und k sind zueinander parallel, aber verschieden.
0 = 3 + 2r r = − 3
2
6. a) Die Richtungsvektoren sind nicht kollinear zueinander.
5 + t = −1 + 4s
t − 4s = −6
0 + 2t = −2 − 2s ; 2t + 2s = −2 1. und 3. Gleichung addieren ergibt:
−t + s = 3
3−t = 6−s
s =1
− 3s = −3 s = 1
2t + 2s = −2 ; t = −s − 1 ; t = −2
t = s−3
t = −2
−t + s = 3
Gemeinsamer Punkt S(3 | −4 | 5)
b) Die Richtungsvektoren sind nicht kollinear zueinander.
0 + 6t = −6 + 6s
6t − 6s = −6
t − s = −1 −1 + 0 = − 1
−4 + 7t = −11 + 7s ; 7t − 7s = −7 ; t − s = −1 ;
t = −1
−5t − 5s = s
5 − 5t = 10 + 5s
t + s = −1
s=0
Gemeinsamer Punkt S(−6 | −11 | 10)
c) Die Richtungsvektoren sind nicht kollinear zueinander.
s = −1t −
4
1 + t = 3 + 4s
0 − t = −2 + 6s ; s = − 1 t +
6
2+t =4
t=2
1
2
1
3
s=0
; s=0
t=2
Gemeinsamer Punkt S(3 | −2 | 4)
190
244
⎛ 15 ⎞
⎛ −2 ⎞
G ⎜ ⎟
7. a) Z. B.: h: x = 26 + r ⋅ ⎜ −3 ⎟ ; r ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ 31 ⎠
⎝ 5⎠
⎛8⎞
⎛1 ⎞
G ⎜ ⎟
b) Z. B.: h: x = 16 + s ⋅ ⎜ −4 ⎟ ; s ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝5⎠
⎝0 ⎠
3 + 2t = 1 + 2s 2t − 2s = −2
8. a) 6 + 4t = 0 + 3s ; 4t − 3s = −6
4+t = 3−s
t + s = −1
Das Doppelte der 3. Gleichung von der 1. Gleichung subtrahieren ergibt:
s =1
s =1
− 4s = −4
3
3
4t − 3s = −6 ; t = s − ; t = − 3
4
2
4
t + s = −1
t = −s − 1
t = −2
Keine gemeinsamen Punkte, Richtungsvektoren nicht kollinear
zueinander.
Die Geraden g, h und k bilden ein Dreieck mit den Eckpunkten
A(3 | −1 | −2), B(5 | 3 | 8), C(−1 | 2 | 0).
0 + t = 1 + 2s t − 2s = 1
t = 2s + 1 t = 3
b)
1= 0+s ;
− s = −1 ; s = 1
; s=1
1+ t = 0 +s
t − s = −1 t = s − 1
t=0
Keine gemeinsamen Punkte, Richtungsvektoren nicht kollinear
zueinander.
5 + t = 2 + 3s
c) 5 + 2t = −1 + s ; Widerspruch
1=0
Keine gemeinsamen Punkte, Richtungsvektoren nicht kollinear
zueinander.
⎛0⎞
⎛4⎞
⎛1⎞
⎛4⎞
G
G
9. a) x = ⎜ 0 ⎟ + t ⋅ ⎜ 2 ⎟ b) x = ⎜ 1 ⎟ + t ⋅ ⎜ 2 ⎟
⎜0⎟
⎜3⎟
⎜1⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎛1⎞
⎛4⎞
G
c) x = ⎜ 1 ⎟ + t ⋅ ⎜ 2 ⎟
⎜0⎟
⎜3⎟
⎝ ⎠
⎝ ⎠
10. g & h: Richtungsvektoren nicht kollinear zueinander.
− p + 2t = 2 + 2s
2t − 2s = p + 2
1 − 8t = 6 − 2s ; −8t + 2s = 5
−2 − 4t = 4p − 4s −4t + 4s = 4p + 2
1. und 2. Gleichung addieren:
− 6t = p + 7
−8t + 2s = 5
−4t + 4s = 4p + 2
Das Doppelte der 2. Gleichung von der 3. Gleichung subtrahieren:
191
244
10. Fortsetzung
− 6t = p + 7
−8t + 2s = 5
12t = 4p − 8
Das Doppelte der 1. Gleichung zur 3. Gleichung addieren:
7
1
− 6t = p + 7
− 6t = p + 7 t = − 6 p − 6 t = −1
−8t + 2s = 5
; −8t + 2s = 5
; s = 4t + 2, 5 ; s = −1, 5
p = −1
p = −1
0 = 6p + 6
p = −1
Für p = −1 schneiden sich die Geraden g und h im Punkt S(−1 | 9 | 2).
11. a) Die Geraden a und b liegen windschief zueinander und bilden kein
Dreieck.
b) A(−8 | −12 | 10); B(6 | 9 | 24); C(−4 | −4 | −2)
AB = 833 ≈ 28,86 ; AC = 244 ≈ 14, 97 ; BC = 945 ≈ 30, 74
12. In der Aufgabenstellung benutzen beide Parameterdarstellungen den
Parameter k. Fabian hat nicht beachtet, dass er einen der beiden Parameter
umbenennen muss, wenn er den Schwerpunkt bestimmen möchte.
(1)
−2 + 3k = 7 + s
(2)
6 − 2k = 4 − 2s
(3)
−3 + 2k = −4 + 3s
Aus (2) folgt k = 1 + s
eingesetzt in (1): s = 3
eingesetzt in (3): s = 3
Die Graphen g und h schneiden sich im Punkt S(10 | −2 | 5).
192
244
⎛3⎞
⎛ −5 ⎞
G ⎜ ⎟
13. a) Z. B. h AB : x = 1 + s ⎜ 3 ⎟ ; s ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝4⎠
⎝ −3 ⎠
g und h AB liegen windschief zueinander.
JJJG ⎛ −5 ⎞ JJJG
JJJG ⎛ 0 ⎞ JJJG
b) Da AB = ⎜ 3 ⎟ = DC und AD = ⎜ −3 ⎟ = BC liegt ein
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝2⎠
⎝ −3 ⎠
Parallelogramm vor.
Schnittpunkt der Diagonalen: (0,5 | 1 | 3,5).
14. a) D(−1 | −1 | 2)
⎛1⎞
⎛ −3 ⎞
G
b) Z. B. g M1C : x = ⎜ −5 ⎟ + s ⎜ −4 ⎟ ; s ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝8⎠
⎝ 7⎠
⎛ −1 ⎞
⎛ −4 ⎞
G
z. B. h M 2 D : x = ⎜ −1 ⎟ + r ⎜ 3 ⎟ ; r ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝2⎠
⎝ −4 ⎠
Schnittpunkt (2,2 | −3,4 | 5,2)
193
244
14. b) Fortsetzung
245
15. a) Aufpunkte stimmen überein, Richtungsvektoren nicht kollinear zueinander. g und h schneiden sich im Punkt P(2 | 1 | −3).
b) Gemeinsamer Aufpunkt O(0 | 0 | 0), Richtungsvektoren nicht kollinear
zueinander. g und h schneiden sich in O(0 | 0 | 0).
16. Richtungsvektor: 80 m tief, 1 500 m westlich, 518 m seitlich
17. a) C(5 | 5 | 0); F(6 | 5 | 1); G(6 | 6 | 0); H(4 | 6 | 1)
b) Die Diagonalen AG und EC schneiden sich im Punkt (4,5 | 5 | 1).
Zeichnung siehe Schülerband.
18. a) G(2 | 4 | 5); H(2 | 2 | 5)
b) Gerade AQ liegt zur Geraden BH windschief.
Gerade AQ schneidet Gerade EP im Punkt (3,75 | 3 | 3,75).
Gerade BH schneidet Gerade EP im Punkt (3,6 | 3,6 | 3).
c) S(3 | 3 | 7,5)
246
19. Das Flugzeug überfliegt das Windrad mit einer Flughöhe von 384 m, d. h.
der vertikale Abstand vom höchsten Punkt des Windrades beträgt 214 m.
194
246
⎛ 8 ⎞ ⎛ −2 ⎞
G ⎜ ⎟ ⎜ ⎟
20. h : x = 4 + t −2 ; t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝0⎠ ⎝ 8 ⎠
⎛ −2 ⎞
⎛1 ⎞
⎜
⎟
Da die Richtungsvektoren Vielfache voneinander sind: −2 = −2 ⎜ 1 ⎟ ,
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ 8⎠
⎝ −4 ⎠
sind die Geraden parallel. Für t = − 12 ergibt sich aus h der Punkt A.
21. a) b = − 23 , c = 43
b) b = − 37 , c = 97
⎛ 1 ⎞ ⎛0 ⎞
G
22. h : x = ⎜ 5 ⎟ + t ⎜ 2 ⎟ ; t ∈ \
⎜⎜
⎟⎟ ⎜⎜ ⎟⎟
⎝ −10 ⎠ ⎝ −4 ⎠
Die Geraden g und h sind parallel aber nicht identisch.
23. a) S(160 | 90 | 0)
⎛ 120 ⎞
JJG
b) FS = ⎜ 120 ⎟ = 120 ⋅ 2 ≈ 169,71 m
⎜⎜
⎟⎟
⎝ 0 ⎠
24. a) Die Geraden sind parallel zueinander.
b) A liegt auf g 5 .
2 Möglichkeiten für Punkt B: B(−18 | −11 | 60) oder B(−2 | −19 | 76).
247
25. a) Das durch das Gleichsetzen von g und h t entstehende Gleichungssystem besitzt für jedes t genau eine Lösung. Der Schnittpunkt in
Abhängigkeit von t ist S t (2 − t | 1 + 2t | −1 + t).
b) t = 15
26. Kristin hat r und s aus (1) und (2) richtig bestimmt aber nicht in Gleichung
(3) kontrolliert. In (3) ergibt sich für r = −4 und s = 4:
−6 = 9 Widerspruch!
Die Geraden sind windschief.
27. a) Nein, es kann zu keine Kollision kommen.
b) Geschwindigkeiten
1. Flugzeug 763,89 km
2. Flugzeug 402,51 km
h
h
28. 5 m über dem Boden.
195
Blickpunkt: Licht und Schatten
249
1. Eckpunkte des Daches:
A(5,0 | −2,4 | 2,4); B(5,0 | 0 | 2,4); C(0 | −2,4 | 2,4); D(0 | 0 | 2,4)
JJJG
JJJG
G
G
Schattenpunkte durch v: z. B. OA ′ = OA + 6 v
5
A ′(7, 4 | 1, 2 | 0); B′(7, 4 | 3, 6 | 0); C′(2, 4 | 1, 2 | 0); D′(2, 4 | 3, 6 | 0)
G
Schattenpunkte durch u:
A ′′(5,8 | −0,8 | 0); B′′(5,8 | 1, 6 | 0); C′′(0,8 | −0,8 | 0); D′′(0,8 | 1, 6 | 0)
Grundstücksgrenze:
⎛1⎞
G
g: x = r ⋅ ⎜ 0 ⎟ ; r ∈ \
⎜0⎟
⎝ ⎠
G
• Bei v liegt der Schatten ganz im Nachbargarten
A = 2,4 m ⋅ 5 m = 12 m 2 .
G
• Bei u liegt der Schatten auf beiden Grundstücken. Er ist begrenzt durch
B′′, D′′, E(5,8 | 0 | 0); F(0,8 | 0 | 0).
A = 1,6 m ⋅ 5 m = 8 m 2
2. a) Koordinaten der Spitze: E (3 | 3 | 5)
⎛ 3⎞
⎛ 2⎞
G ⎜ ⎟
Lichtstrahl durch E: g: x = 3 + λ ⋅ ⎜ 3 ⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ 5⎠
⎝ −2 ⎠
In der x1 -x 2 -Ebene gilt x3 = 0
→ λ = 2,5 → E’(8 | 10,5 | 0).
196
249
2. b) Schatten an der Wand (x1 -x3 -Ebene)
Berechnung von E’ in der x1 -x 2 -Ebene :
⎛ 3⎞
⎛ 0, 5 ⎞
G
g: x = ⎜ 3 ⎟ + λ ⎜ −2 ⎟ , x3 = 0 → λ = 5
⎜⎜ ⎟⎟
⎜⎜
⎟⎟
⎝ 5⎠
⎝ −1 ⎠
E’ (5,5 | −7 | 0)
E’ liegt „hinter“ der x1 -x3 -Ebene . Die „Knickstelle“ des Schattens
erhält man durch Schnitt der Geraden E’B mit der x1 -Achse .
⎛ 5⎞
⎛ 0, 5 ⎞
⎛1⎞
⎜ 5 ⎟ + λ ⋅ ⎜ −12 ⎟ = r ⋅ ⎜ 0 ⎟ → x ≈ 5, 2
1
⎜⎜ ⎟⎟
⎜⎜
⎟⎟
⎜⎜ ⎟⎟
⎝0⎠
⎝ 0 ⎠
⎝0⎠
Schattenpunkt am Boden: (5,5 | −7 | 0)
Schattenpunkt an der: (3,75 | 0 | 3,5)
Knickstellen: (1,5625 | 0 | 0); (5,21 | 0 | 0)
197
249
2. c) Schattenpunkt am Boden: (6 | 4 | 0)
3. a) A (6 | 4 | 0); B (6 | 6 | 0); C (4 | 6 | 0); D (4 | 4 | 0); E (6 | 4 | 3);
F (6 | 6 | 3); G (4 | 6 | 3); H (4 | 4 | 3); S (5 | 5 | 6)
b)
198
249
3. b) Fortsetzung
S: Schattenpunkt am Boden: (−5 | 11 | 0)
Schattenpunkt an der x 2 -x3 -Ebene: (0 | 8 | 3)
E: Schattenpunkt am Boden: (1 | 7 | 0)
Schattenpunkt an der Wand (0 | 7,6 | −0,6)
(er wirft also keinen „direkten“ Schatten)
F: Schattenpunkt am Boden: (1 | 9 | 0)
„Schattenpunkt“ an der Wand (0 | 9,6 | −0,6)
(existiert aber eigentlich nicht)
G: Schattenpunkt am Boden: (−1 | 9 | 0)
Schattenpunkt an der Wand: (0 | 8,4 | 0,6)
H: Schattenpunkt am Boden: (−1 | 7 | 0)
Schattenpunkt an der Wand: (0 | 6,4 | 0,6)
Knickstellen: (0 | 7 | 0) und (0 | 9 | 0)
Der Schatten wird also durch die Punkte (1 | 7 | 0); (0 | 7 | 0);
(0 | 6,4 | 0,6); (0 | 8 | 3); (0 | 8,4 | 0,6); (0 | 9 | 0) und (1 | 9 | 0)
beschrieben.
c)
Schattenpunkte:
E ′(7, 7 | 5, 7 | 0); F′(7, 7 | 8, 6 | 0); G ′(4, 9 | 8, 6 | 0);
H ′(4, 9 | 5, 7 | 0); S′(9, 5 | 12, 5 | 0)
199
249
4.
Schattenpunkte
E1 in x1 -x 2 -Ebene:
E1 (6,5 | −13 | 0)
E 2 auf der Stufe:
E 2 (5 | −8 | 2)
Bx1 in x1 -x 2 -Ebene:
Bx1 (5,18 | −4 | 0)
Bx 2 auf der Stufe:
Bx 2 (4,4 | −4 | 2)
D x1 in x1 -x 2 -Ebene:
D x1 (2 | −4 | 0)
D x 2 auf der Stufe:
D x 2 (3 | −4 | 2)
4.3 Winkel im Raum
4.3.1 Orthogonalität zweier Vektoren − Skalarprodukt
252
253
G G
2. u ∗ u = u1 ⋅ u1 + u 2 ⋅ u 2 + u 3 ⋅ u 3 = u12 + u 2 2 + u 3 2
G
Nach Seite 220 (Schülerband) Satz 1 ist u = u12 + u 2 2 + u 3 2 .
G
G G
Einsetzen der ersten Gleichung liefert u = u ∗ u .
G G
G G
3. (1) u ∗ v = 0 und v ∗ u = 0
G G
(2) 3 ⋅ ( u ∗ v ) = 0;
G G
(3 ⋅ u) ∗ v = 0;
G
G
u ∗ (3 ⋅ v) = 0
200
253
G G G
3. (3) u ∗ ( v + w ) = −1;
G G G G
u ∗ v + u ∗ w = −1
Alle Ausdrücke sind jeweils gleich.
Die Eigenschaften sind:
(1) kommutativ
(2) assoziativ bzgl. Multiplikation mit Skalar
(3) distributiv bzgl. Vektoraddition
4. (1) Die Funktion „dotP“ berechnet direkt das Skalarprodukt zweier
Vektoren, die als Listen ({ …}) oder Vektoren angegeben sind.
Ergebnis: −7,26
(2) Die Vektoren werden als Listen gespeichert.
Die Multiplikation arbeitet elementweise und danach werden die
Ergebnisse aufsummiert.
Ergebnis: −5125,2906
(3) Wie in (2), jedoch ohne das vorherige Speichern der einzelnen Vektoren
als Listen.
Ergebnis: −262,4536
5. Korrektur: In der 1. Auflage waren die Bezeichnungen der Vektoren
G
G
a und b im Foto vertauscht.
a) Verwende die Umkehrung des Satzes des Pythagoras:
⎛ −0,5 ⎞ ⎛ 0 ⎞
⎛ −0,5 ⎞
JJJG
a = CB = ⎜ 2 ⎟ − ⎜ 0 ⎟ = ⎜ 2 ⎟ = 0, 25 + 4 + 576 = 580, 25
⎜ 24 ⎟ ⎜ 0 ⎟
⎜ 24 ⎟
⎝
⎠ ⎝ ⎠
⎝
⎠
⎛ 10 ⎞ ⎛ 0 ⎞
⎛ 10 ⎞
JJJG
b = CA = ⎜ 2,5 ⎟ − ⎜ 0 ⎟ = ⎜ 2,5 ⎟ = 100 + 6, 25 + 0 = 106, 25
⎜ 0 ⎟ ⎜ 0⎟
⎜ 0 ⎟
⎝
⎠ ⎝ ⎠
⎝
⎠
⎛ −0,5 ⎞ ⎛ 10 ⎞
⎛ −10,5 ⎞
JJJG
c = AB = ⎜ 2 ⎟ − ⎜ 2,5 ⎟ = ⎜ −0,5 ⎟ = 110, 25 + 0, 25 + 576
⎜ 24 ⎟ ⎜ 0 ⎟
⎜ 24 ⎟
⎝
⎠ ⎝
⎠
⎝
⎠
= 686,5
⇒ a 2 + b 2 = 686,5 = c 2
Der Satz des Pythagoras ist erfüllt. Damit ist das Dreieck rechtwinklig.
G G
G2 G2
b) Pythagoras a − b = a + b gilt bei Orthogonalität
⇔ ( a1 − b1 ) + ( a 2 − b 2 ) + ( a 3 − b 3 )
2
2
2
= a12 + a 2 2 + a 33 + b12 + b 2 2 + b 33
⇔ a1b1 + a 2 b 2 + a 3 b 3 = 0
G G
⇔ a∗b = 0
Bedingung für Orthogonalität zweier Vektoren:
Das Skalarprodukt der Vektoren muss verschwinden.
201
253
6. a)
b)
c)
d)
G G
u∗v
G G
u∗v
G G
u∗v
G G
u∗v
=
=
=
=
0+0+0 = 0
2 +1− 3 = 0
2 − 4 + 15 = 13
6+0−6 = 0
⇒ orthogonal
⇒ orthogonal
⇒ nicht orthogonal
⇒ orthogonal
7. a) Es wurden lediglich die Komponenten multipliziert aber die Ergebnisse
nicht addiert. Das Skalarprodukt ergibt eine Zahl.
b) Hier wurde falsch addiert.
254
JJJG ⎛ 4 ⎞ JJJG ⎛ 3 ⎞
8. AC = ⎜ 2 ⎟ ; BD = ⎜ 3 ⎟
⎜ −6 ⎟
⎜ 3⎟
⎝ ⎠
⎝ ⎠
JJJG JJJG
AC ∗ BD = 12 + 6 − 18 = 0
Die Diagonalen sind orthogonal zueinander.
Das Viereck ist ein Drachenviereck.
b) t = 1 oder t = 1
9. a) t = 3
2
c) t = 0 oder t = 6
⎛ 0 ⎞ ⎛ 2 ⎞ ⎛ −3 ⎞
10. Beispiele: ⎜ 3 ⎟ ; ⎜ 4 ⎟ ; ⎜ 0 ⎟
⎜ 2⎟ ⎜ 0⎟ ⎜ 4 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
Es gibt unendlich viele, da es zum einen bereits unendlich viele Vielfache
von einem Vektor gibt. Zum anderen kann man stets 2 orthogonale
G
Vektoren addieren und das Ergebnis ist erneut orthogonal zu v.
⎛0⎞
11. a) (1) z. B. ⎜ 1 ⎟ ;
⎜ 2⎟
⎝ ⎠
⎛2⎞
⎜ −1⎟ ;
⎜0⎟
⎝ ⎠
⎛ −1⎞
⎜ 0 ⎟;
⎜1⎟
⎝ ⎠
⎛ 3⎞
⎜1⎟
⎜ 5⎟
⎝ ⎠
⎛ 4 ⎞ ⎛ −8 ⎞
⎜ 2 ⎟; ⎜ 7 ⎟
⎜ −3 ⎟ ⎜ 6 ⎟
⎝ ⎠ ⎝ ⎠
⎛1⎞ ⎛ 0⎞ ⎛ 2⎞ ⎛ 3⎞
(3) z. B. ⎜ 0 ⎟ ; ⎜ 0 ⎟ ; ⎜ 0 ⎟ ; ⎜ 0 ⎟
⎜ 0⎟ ⎜1⎟ ⎜ 0⎟ ⎜ 4⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎛ −1⎞ ⎛ 0 ⎞ ⎛ 1 ⎞ ⎛ −2 ⎞
(4) z. B. ⎜ 1 ⎟ ; ⎜ −1⎟ ; ⎜ 1 ⎟ ; ⎜ 1 ⎟
⎜ 0 ⎟ ⎜ 1 ⎟ ⎜ −2 ⎟ ⎜ 1 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎛0⎞
(2) z. B. ⎜ 1 ⎟ ;
⎜0⎟
⎝ ⎠
⎛ −4 ⎞
⎜ 0 ⎟;
⎜ 3⎟
⎝ ⎠
b) Im Raum und in der Ebene sind alle Vielfachen eines Vektors, der
orthogonal zum gegebenen ist, ebenfalls orthogonal.
Im Raum steht zudem jeder Vektor, der in einer bestimmten orthogonalen Ebene liegt, orthogonal zu dem gegebenen Vektor.
202
254
12. a) Skalarprodukt der Richtungsvektoren:
⎛ −1⎞ ⎛ 7 ⎞
⎜ 3 ⎟ ∗ ⎜ −1⎟ = 0 ⇒ Geraden orthogonal
⎜5⎟ ⎜2⎟
⎝ ⎠ ⎝ ⎠
Gleichsetzen der Parameterdarstellungen liefert für r = −1 bzw. s = 1
den Schnittpunkt S(2 | 1 | 1).
b) Skalarprodukt der Richtungsvektoren:
⎛4⎞ ⎛ 5⎞
⎜ 2 ⎟ ∗ ⎜ −7 ⎟ = 1 ⇒ nicht orthogonal
⎜ −1⎟ ⎜ 5 ⎟
⎝ ⎠ ⎝ ⎠
Gleichsetzen der Parameterdarstellungen ergibt keine Lösung für r, s
⇒ kein Schnittpunkt
c) Skalarprodukt der Richtungsvektoren:
⎛ 1 ⎞ ⎛ 2⎞
⎜ −1⎟ ∗ ⎜ 2 ⎟ = 0 ⇒ Geraden orthogonal
⎜ 2 ⎟ ⎜ 0⎟
⎝ ⎠ ⎝ ⎠
Gleichsetzen der Parameterdarstellungen ergibt keine Lösung für r, s
⇒ kein Schnittpunkt
−4
G JJJG ⎛ 8 ⎞
G JJJG ⎛ ⎞
c = AB = ⎜ 3 ⎟
b = CA = ⎜ 0 ⎟
⎜1⎟
⎜ −c ⎟
⎝ ⎠
⎝ 3⎠
G G
2
Rechter Winkel bei C ⇒ a ∗ b = 0 ⇔ c 3 − c 3 + 32 = 0; keine Lösung
G G
Rechter Winkel bei B ⇒ a ∗ c = 0 ⇔ c 3 = −6
G G
Rechter Winkel bei A ⇒ b ∗ c = 0 ⇔ c 3 = −32
4 ⎞
G JJJG ⎛
13. a = CB = ⎜ 3 ⎟
⎜1 − c ⎟
3⎠
⎝
−2
0
2
G JJJG ⎛ ⎞ G JJJG ⎛ ⎞ G JJJG ⎛ ⎞
14. a) (1) a = CB = ⎜ −2 ⎟ ; b = CA = ⎜ 0 ⎟ ; c = AB = ⎜ 2 ⎟
⎜ 2⎟
⎜ −2 ⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
G
G
G
a = b = c = 8 ⇒ gleichseitig
−5
−1
−4
G JJJG ⎛ ⎞ G JJJG ⎛ ⎞ G JJJG ⎛ ⎞
(2) a = CB = ⎜ 1 ⎟ ; b = CA = ⎜ 4 ⎟ ; c = AB = ⎜ −3 ⎟
⎜ −3 ⎟
⎜ −6 ⎟
⎜ 3⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
alle Skalarprodukte ungleich 0 und
G
G
G
a = 35; b = 53; c = 34 ; keine Besonderheiten
0
0
0
G JJJG ⎛ ⎞ G JJJG ⎛ ⎞ G JJJG ⎛ ⎞
(3) a = CB = ⎜ −3 ⎟ ; b = CA = ⎜ 0 ⎟ ; c = AB = ⎜ −3 ⎟
⎜0⎟
⎜ 3⎟
⎜ −3 ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
G G
a ∗ b = 0 ⇒ rechter Winkel bei C;
G
G
G
a = b = 3; c = 3 2 ⇒ gleichschenklig
203
254
JJJG JJJG JJJG JJJG
JJJG JJJG
14. b) (1) Eines der Skalarprodukte AB ∗ BC; AB ∗ CA oder BC ∗ CA
muss null ergeben, dann ist das Dreieck rechtwinklig.
JJJG
JJJG
(2) Das Dreieck ist gleichschenklig, falls von AB = BC oder
JJJG
JJJG
JJJG
JJJG
AB = CA oder BC = CA genau eine Gleichung erfüllt ist.
JJJG
JJJG
JJJG
(3) Das Dreieck ist gleichseitig, falls AB = BC = CA gilt.
JJJG ⎛ 4 ⎞
JJJG ⎛ 4 ⎞
15. AB = ⎜ −3 ⎟
AC = ⎜ 3 ⎟
⎜ −1,5 ⎟
⎜ −1,5 ⎟
⎝
⎠
⎝
⎠
JJJG JJJG
AB ∗ AC = 16 − 9 + 2, 25 = 9, 25 ≠ 0
Die Vektoren sind nicht orthogonal zueinander, es wird kein rechter
Winkel eingeschlossen.
255
G
G G
G G
16. a) Gesucht x mit x ∗ v = 0 und x ∗ u = 0
x2 + x3 = 0
⇒ LGS
x1 + x 2 − x 3 = 0
Lösungsmenge L = {(2t | − t | t) | t ∈ \}
2t
G ⎛ ⎞
⇒ alle Vektoren x = ⎜ − t ⎟ ; t ∈ \ sind Lösungen.
⎜ t ⎟
⎝ ⎠
b) Es gibt unendlich viele Lösungen, die alle in einer Ebene liegen.
G
Verfahren: Wähle 2 Komponenten von u beliebig und bestimme die
G G
3., sodass u ∗ v = 0 .
1
G ⎛ ⎞
Beispiel u = ⎜ 2 ⎟
⎜0⎟
⎝ ⎠
G
Berechne w analog zu a)
Beispiel: w 1 + 2w 2 = 0 und 2w 1 − w 2 + 2w 3 = 0
Wähle w 1 = 2, dann ist w 2 = −1; w 3 = −2,5
2 ⎞
G ⎛
w = ⎜ −1 ⎟
⎜ −2,5 ⎟
⎝
⎠
G G
17. v ∗ u = 0 ⇒ 2a − b = 0 ⇒ L =
{( t ) | t ∈ \}
t
2
⇒ a = t , b = t mit t ∈ \ .
2
Beispiele: a = 1; b = 2 oder a = 2; b = 4 oder a = 0; b = 0
204
255
18. Nach dem gemischten Assoziativgesetz (Satz 2) ist
G
G
G
G G
( raG ) ∗ ( sb ) = r ( aG ∗ ( sb ) ) = r ( s ⋅ aG ∗ b ) = rs ⋅ aN
∗b = 0
=0
19. Vektor Balken 1:
Vektor Balken 2:
0, 2 ⎞ ⎛ 0 ⎞ ⎛ 0, 2 ⎞
G ⎛
a = ⎜ 6 ⎟−⎜ 0 ⎟ = ⎜ 6 ⎟
⎜ −5 ⎟ ⎜ −2 ⎟ ⎜ −3 ⎟
⎝
⎠ ⎝ ⎠ ⎝
⎠
−
−
0,1
0
0,1
⎛
⎞
⎛
⎞
⎛
⎞
G
b = ⎜ −3 ⎟ − ⎜ 0 ⎟ = ⎜ −3 ⎟
⎜ −6 ⎟ ⎜ −2 ⎟ ⎜ −4 ⎟
⎝
⎠ ⎝ ⎠ ⎝
⎠
G G
a ∗ b = −0, 02 − 18 + 12 = −6, 02 ≠ 0
Die Balken sind nicht orthogonal.
20. Darstellungen der Vektoren
JJG ⎛ 0 ⎞ JJG ⎛ −4 ⎞ JJG ⎛ 3 ⎞ JJG ⎛ 0 ⎞
v1 = ⎜ −3 ⎟ ; v 2 = ⎜ 0 ⎟ ; v 3 = ⎜ 0 ⎟ ; v 4 = ⎜ −3 ⎟
⎜ −4 ⎟
⎜ 3⎟
⎜ 4⎟
⎜0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎝ ⎠
JJG JJG
v1 ∗ v 2 = −12
nicht orthogonal
JJG JJG
nicht orthogonal
v1 ∗ v 3 = −16
JJG JJG
v1 ∗ v 4 = 9
nicht orthogonal
JJG JJG
v 2 ∗ v3 = 0
orthogonal
JJG JJG
orthogonal
v2 ∗ v4 = 0
JJG JJG
v3 ∗ v 4 = 0
orthogonal
21. Bei der Verwendung des ∗ als Skalarproduktzeichen hat Jenny Recht.
(Bei der auch üblichen Verwendung eines „normalen“ Malpunktes für das
Skalarprodukt wäre Tims Aussage korrekt und Jennys Argumentation
falsch.)
22. Wähle D so, dass alle 4 Skalarprodukte null sind.
JJJG ⎛ 0 ⎞ JJJG ⎛ −3 ⎞ JJJG ⎛ −3 ⎞
AB = ⎜ 5 ⎟ ; CB = ⎜ 0 ⎟ ; CA = ⎜ −5 ⎟
⎜0⎟
⎜ −4 ⎟
⎜ −4 ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
JJJG JJJG
Rechter Winkel bei B, da AB ⋅ CB = 0.
JJJG ⎛ d1 − 1 ⎞ JJJG ⎛ 4 − d1 ⎞
Sei D ( d1 | d 2 | d 3 ) ⇒ AD = ⎜ d 2 − 1 ⎟ ; CD = ⎜ 6 − d 2 ⎟
⎜
⎟
⎜
⎟
⎝ d3 − 2 ⎠
⎝ 6 − d3 ⎠
JJJG JJJG
JJJG JJJG
JJJG JJJG
AD ∗ CD = 0; AD ∗ AB = 0 und CD ∗ CB = 0 .
205
255
22. Fortsetzung
JJJG
Bestimmung der Koordinaten über Parallelverschiebung von A entlang BC
⎛1⎞ ⎛ 3⎞ ⎛ 4⎞
D = ⎜1⎟ + ⎜0⎟ = ⎜1⎟
⎜ 2⎟ ⎜ 4⎟ ⎜ 6⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
JJJG
JJJG
JJJG
JJJG
Alle Seitenlängen sind wegen AB = CB = AD = CD = 5 gleich lang.
Also ist ABCD ein Quadrat.
JJJG ⎛ −1,85 ⎞ JJJG ⎛ −1,3 ⎞ JJJG ⎛ −0,55 ⎞
23. CB = ⎜ 1, 4 ⎟ ; CA = ⎜ −1, 75 ⎟ ; AB = ⎜ 3,15 ⎟
⎜ −0,19 ⎟
⎜ −0,32 ⎟
⎜ 0,13 ⎟
⎝
⎠
⎝
⎠
⎝
⎠
JJJG JJJG
JJJG JJJG
JJJG JJJG
AB ∗ CB = 5, 4028
CB ∗ CA = 0, 0158
CA ∗ AB = −4,84
Bei Punkt C liegt „annähernd“ ein rechter Winkel vor.
24. C(6 − 2r | 4 + r | 5 + 2r)
JJJG JJJG
Rechter Winkel bei C ⇔ AC ∗ BC = 0
JJJG ⎛ 3 − 2r ⎞ JJJG ⎛ −1 − 2r ⎞
AC = ⎜ 2 + r ⎟ ; BC = ⎜ 8 + r ⎟
⎜ 6 + 2r ⎟
⎜ −1 − 2r ⎟
⎝
⎠
⎝
⎠
JJJG JJJG
2
AC ∗ BC = 9r + 16r + 7 = 0 ⇔ r1 = −1 oder r2 = − 7
⇒ C1 (8 | 3 | 3) oder
(
C 2 68
9
29
9
31
9
9
)
4.3.2 Winkel zwischen zwei Vektoren
257
2. (In 1. Auflage: Nr. 3)
cos ϕ1 =
⎛ 8 ⎞ ⎛2⎞
⎜ −8 ⎟ ∗⎜ 10 ⎟
⎜ −4 ⎟ ⎜ 11 ⎟
⎝ ⎠ ⎝ ⎠
⎛8⎞
⎜ −8 ⎟
⎜ ⎟
⎝ −4 ⎠
⎛2⎞
⋅ ⎜ 10 ⎟
⎜ ⎟
⎝ 11 ⎠
= −20 = − 1
12 ⋅ 15
9
⇒ ϕ1 = 96,38° stumpfer Winkel
⇒ ϕ 2 = 180° − ϕ1 = 83, 62° spitzer Winkel
258
3. (In 1. Auflage: Nr. 4)
a) Die ersten beiden Schritte erwarten die Eingabe der Vektoren.
Der 3. Schritt wertet direkt die Formel α = cos −1
(
G G
a ∗b
G G
a ⋅ b
Im letzten Schritt erfolgt die Ausgabe des Winkels α.
) aus.
206
258
3. b)
4. (In 1. Auflage: Nr. 5)
G JJJG
G JJJG
Berechne den Winkel zwischen den Vektoren u = AB und v = AC
8
2
G ⎛ ⎞ G ⎛ ⎞
mit u = ⎜ −8 ⎟ ; v = ⎜ 10 ⎟ .
⎜ −4 ⎟
⎜ 11 ⎟
⎝ ⎠
⎝ ⎠
G
G G
G
G G
u = u ∗ u = 144 = 12 ; v = v ∗ v = 225 = 15
G G
u ∗ v = −108
Winkel berechnen: cos ϕ =
−108
12 ⋅ 15
= −0, 6 ⇒ ϕ = 126,9°
5. (In 1. Auflage: Nr. 6)
α = cos −1
(
G G
u ∗v
G G
u ⋅ v
)
a) α = 82,388°
b) α = 107,024°
c) α = 149,163°
6. (In 1. Auflage: Nr. 7)
G
G
a) u = 3 und v = 3
⇒ Alle Seiten des Vierecks sind gleich lang ⇒ Raute.
b) A(1 | 1 | 2)
JJJG JJJG G ⎛ 3 ⎞
OB = OA + u = ⎜ 0 ⎟ ⇒ B(3 | 0 | 4)
⎜ 4⎟
⎝ ⎠
JJJG JJJG G ⎛ 2 ⎞
OC = OA + v = ⎜ 3 ⎟ ⇒ C(2 | 3 | 0)
⎜0⎟
⎝ ⎠
JJJG JJJG G G ⎛ 4 ⎞
OD = OA + u + v = ⎜ 2 ⎟ ⇒ D(4 | 2 | 2)
⎜ 2⎟
⎝ ⎠
cos ϕ =
JJJG JJJG
AD ∗ BC
JJJG JJJG
AD ⋅ BC
⇒ ϕ = 90°
=
⎛ 3 ⎞ ⎛ −1 ⎞
⎜ 1 ⎟ ∗⎜ 3 ⎟
⎜ 0 ⎟ ⎜ −4 ⎟
⎝ ⎠ ⎝ ⎠
10 ⋅
26
=0
207
258
7. (In 1. Auflage Nr. 8)
a) S(5 | 4 | −5); α = 63,069°
b) S(−4 | −3 | −1); α = 46,077°
c) S(−8 | 7 | −5); α = 83,845°
d) S(−15 | 9 | 9); α = 68,301°
8. (In 1. Auflage Nr. 9)
Der Winkel berechnet sich aus cos α =
G G
u ∗v
G G
u ⋅ v
.
Das Vorzeichen von cos x hängt nur vom Skalarprodukt ab.
Da cos α > 0 für 0° ≤ α < 90° und cos α < 0 für 90° < α ≤ 180° ist,
ist die Aussage korrekt.
259
9. (In 1. Auflage Nr. 10)
JJJG ⎛ −3 ⎞ JJJG ⎛ −3 ⎞ JJJG ⎛ 0 ⎞
a) AB = ⎜ 4 ⎟ ; AC = ⎜ 0 ⎟ ; BC = ⎜ −4 ⎟
⎜0⎟
⎜5⎟
⎜ 5⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
JJJG
JJJG
JJJG
Längen: AB = 25 = 5; AC = 34 ≈ 5,831; BC = 41 = 6, 403
Winkel bei A: α = 72,02°
Winkel bei B: β = 60,02°
Winkel bei C: γ = 47,96°
JJJG ⎛ 1 ⎞ JJJG ⎛ 3 ⎞ JJJG ⎛ 2 ⎞
b) AB = ⎜ −2 ⎟ ; AC = ⎜ 4 ⎟ ; BC = ⎜ 6 ⎟
⎜ 4⎟
⎜9⎟
⎜ 5⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
Längen:
JJJG
JJJG
JJJG
AB = 21 ≈ 4,583; AC = 106 ≈ 10, 296; BC = 65 ≈ 8, 062
Winkel bei A: α = 48,925°;
Winkel bei B: β = 105,704°
Winkel bei C: γ = 25,371°
JJJG ⎛ 1 ⎞ JJJG ⎛ −3 ⎞ JJJG ⎛ −4 ⎞
c) AB = ⎜ 1 ⎟ ; AC = ⎜ 3 ⎟ ; BC = ⎜ 2 ⎟
⎜0⎟
⎜ −2 ⎟
⎜ −2 ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
Längen:
JJJG
JJJG
AB = 2 ≈ 1, 414; AC =
Winkel bei A: α = 90°
Winkel bei B: β = 73,22°
Winkel bei C: γ = 16,78°
JJJG
22 ≈ 4, 690; BC =
24 ≈ 4,90
208
259
10. (In 1. Auflage Nr. 11)
Koordinatenursprung z. B. links unten hinten, Achsen x1 nach vorn,
x 2 nach rechts, x 3 nach oben.
Dann: P(12 | 2 | 12); Q(12 | 12 | 4); R(10 | 12 | 12)
JJJG ⎛ 0 ⎞ JJJG ⎛ −2 ⎞ JJJG ⎛ −2 ⎞
PQ = ⎜ 10 ⎟ ; PR = ⎜ 10 ⎟ ; QR = ⎜ 0 ⎟
⎜ −8 ⎟
⎜ 0⎟
⎜8⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
Innenwinkel:
Bei P: α = 40,03°; bei Q: β = 52,70°; bei R: γ = 87,27°
11. (In 1. Auflage Nr. 12)
Gleichsetzen der Geraden führt auf folgendes Gleichungssystem in
Matrixschreibweise:
⎛ 2 −1 −2 ⎞
⎛1 0
−2 ⎞
⎜ −1 −3 8 ⎟ ⇒ ⎜ 0 1
−2 ⎟
⎜
⎟
⎜
⎟
−
− 5⎠
3
a
4
0
0
a
⎝
⎠
⎝
Das System besitzt für a = 5 die Lösung r = −2, s = −2.
⇒ S(2 | −8 | −9)
1
2
G ⎛ ⎞
G ⎛ ⎞
Schnittwinkel aus Richtungsvektoren u = ⎜ −1⎟ und v = ⎜ 3 ⎟ ; α = 50,77°
⎜3⎟
⎜5⎟
⎝ ⎠
⎝ ⎠
12. (In 1. Auflage Nr. 13)
Ein Würfel hat 4 Raumdiagonalen, z. B. dargestellt durch
8
8
−8
−8
G ⎛ ⎞ G ⎛ ⎞ G ⎛ ⎞ G ⎛ ⎞
a = ⎜ 8 ⎟ ; b = ⎜ −8 ⎟ ; c = ⎜ − 8 ⎟ ; d = ⎜ 8 ⎟ .
⎜8⎟
⎜8⎟
⎜8⎟
⎜8⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎝ ⎠
Da der Würfel symmetrisch ist, reicht es einen Schnittwinkel zu berechnen,
z. B. α = cos −1
(
G G
a ∗b
G G
a ⋅ b
) = 70,53° .
13. (In 1. Auflage Nr. 14)
⎛ k − 2⎞
JJJG ⎛ 5 ⎞ JJJG ⎛ k + 3 ⎞ JJJG ⎛ k − 2 ⎞
C k = ⎜ −2 ⎟ ⇒ AB = ⎜ −1 ⎟ ; AC = ⎜ −1 ⎟ ; BC = ⎜ 0 ⎟
⎜ 7 ⎟
⎜ −2 ⎟
⎜ 0 ⎟
⎜ 2 ⎟
⎝
⎠
⎝ ⎠
⎝
⎠
⎝
⎠
JJJG JJJG
rechter Winkel bei A: AB ∗ AC = 0 ⇔ 16 + 5k = 0 ⇔ k1 = − 16
5
JJJG JJJG
14
rechter Winkel bei B: AB ∗ BC = 0 ⇔ −14 + 5k = 0 ⇔ k 2 =
5
rechter Winkel bei C:
JJJG JJJG
AC ∗ BC = 0 ⇔ (k + 3)(k − 2) = 0 ⇔ k 3 = 2, k 4 = −3
209
259
14. (In 1. Auflage Nr. 15)
G
G
G
G
u und v parallel ⇒ u = r ⋅ v; r ∈ \ \ {0}
Satz 3: cos α =
G G
ru∗u
G
G
u ⋅ ru
=
G2
r u
G2
r ⋅ u
=
r
r
Für r > 0 ist cos α = 1 ⇒ α = 0°.
Für r < 0 ist cos α = −1 ⇒ α = 180°.
⇒ Satz 3 liefert korrekte Ergebnisse.
15. (In 1. Auflage Nr. 16)
cos ϕ1 =
⎛1⎞ G
⎜0⎟ ∗ v
⎜ ⎟
⎝0⎠
G ;
1⋅ v
cos ϕ 2 =
⎛ 0⎞ G
⎜1⎟ ∗ v
⎜ ⎟
⎝ 0⎠
G ;
1⋅ v
cos ϕ3 =
⎛ 0⎞ G
⎜ 0⎟ ∗ v
⎜ ⎟
⎝1⎠
G
1⋅ v
2
G ⎛ ⎞
a) v = ⎜ 1 ⎟ : ϕ1 = 64,12°; ϕ 2 = 77, 40°; ϕ 3 = 29, 21°
⎜ 4⎟
⎝ ⎠
−2
G ⎛ ⎞
v = ⎜ 3 ⎟:
⎜ 5⎟
⎝ ⎠
−2
G ⎛ ⎞
v = ⎜ 1 ⎟:
⎜ −4 ⎟
⎝ ⎠
−2
G ⎛ ⎞
v = ⎜ −3 ⎟ :
⎜ −5 ⎟
⎝ ⎠
⎛v ⎞
G ⎜ 1⎟
v = v2 :
⎜ ⎟
⎝ v3 ⎠
ϕ1 = 71, 07°; ϕ 2 = 60,88°; ϕ3 = 35,80°
ϕ1 = 64,12°; ϕ 2 = 77, 40°; ϕ3 = 29, 21°
ϕ1 = 71, 07°; ϕ 2 = 60,88°; ϕ3 = 35,80°
ϕ1 = arccos
v1
2
v1 + v 2 2 + v 2 2
; ϕ 2 = arccos
ϕ3 = arccos
v3
2
v1 + v 2 2 + v 2 2
;
⎛ v1 ⎞
G
v1
b) Mit v = ⎜ v 2 ⎟ ist cos 2 ( ϕ1 ) = ⎛
⎜ v 2 +v 2 +v 2
⎜ ⎟
2
3
⎝ 1
⎝ v3 ⎠
ebenso cos 2 ( ϕ 2 ) =
v22
2
v1 + v 2 2 + v 3 2
2
2
;
v1
⎞ =
und
⎟
v12 + v 2 2 + v 3 2
⎠
und cos 2 ( ϕ3 ) =
v32
2
v1 + v 2 2 + v 3 2
Aufsummieren ergibt:
cos 2 ( ϕ1 ) + cos 2 ( ϕ 2 ) + cos 2 ( ϕ3 ) =
v2
2
v1 + v 2 2 + v 2 2
v12 + v 2 2 + v 3 2
v12 + v 2 2 + v 3 2
=1
.
210
259
16. (In 1. Auflage Nr. 17)
JJG G
Kraft in Wegrichtung Fs = F ⋅ cos α
JJG
Fs = 120 N cos 35° = 98,3 N
G G JJG G
physikalische Arbeit: W = F ∗ s = Fs ⋅ s
W = 98,3 N ⋅ 300 m = 29 489,5 Nm
4.3.3 Vektorprodukt
262
G
G
2. (1) a und b Vielfache voneinander:
G
G
b = r ⋅ a; r ∈ \ \ {0}
⎛ a 2 ra 3 − a 3 ra 2 ⎞ G
G G G G
a × b = a × ra = ⎜ a 3 ra1 − a1ra 3 ⎟ = 0
⎜
⎟
⎝ a1ra 2 − a 2 ra1 ⎠
G G ⎛ b 2 a 3 − b 3a 2 ⎞ ⎛ − a 2 b 3 + a 3 b 2 ⎞
(2) b × a = ⎜ b 3a 1 − b1a 3 ⎟ = ⎜ − a 3 b1 + a1b 3 ⎟
⎜
⎟ ⎜
⎟
⎝ b1a 2 − b 2 a1 ⎠ ⎝ − a1b 2 + a 2 b1 ⎠
⎛ a 2 b 3 − a 3b 2 ⎞
G G
= − ⎜ a 3 b1 − a1b 3 ⎟ = − a × b
⎜
⎟
⎝ a1b 2 − a 2 b1 ⎠
⎛ a 2 ( b3 + c3 ) − a 3 ( b 2 + c 2 ) ⎞
G (G G) ⎜
⎟
(3) a × b + c = ⎜ a 3 ( b1 + c1 ) − a1 ( b 3 + c 3 ) ⎟
⎜ a (b + c ) − a (b + c ) ⎟
2
2 1
1 ⎠
⎝ 1 2
⎛ a 2 b 3 − a 3 b 2 + a 2 c 3 − a 3c 2 ⎞
= ⎜ a 3 b1 − a1b 3 + a 3c1 − a1c 3 ⎟
⎜
⎟
⎝ a1b 2 − a 2 b1 + a1c 2 − a 2 c1 ⎠
⎛ a 2 b 3 − a 3 b 2 ⎞ ⎛ a 2 c 3 − a 3c 2 ⎞
G G G G
= ⎜ a 3 b1 − a1b 3 ⎟ + ⎜ a 3c1 − a1c 3 ⎟ = a × b + a × c
⎜
⎟ ⎜
⎟
⎝ a1b 2 − a 2 b1 ⎠ ⎝ a1c 2 − a 2 c1 ⎠
⎛ a 2 rb 3 − a 3 rb 2 ⎞ ⎛ r ( a 2 b 3 − a 3 b 2 ) ⎞
G
G
G G
⎜
⎟
(4) a × ( r ⋅ b ) = ⎜ a 3 rb1 − a1rb 3 ⎟ = ⎜ r ( a 3 b1 − a1b 3 ) ⎟ = r ( a × b )
⎜
⎟
⎝ a1rb 2 − a 2 rb1 ⎠ ⎜⎝ r ( a1b 2 − a 2 b1 ) ⎟⎠
JJJG
3. Nach Satz 8 ist der Flächeninhalt eines Parallelogramms, das von AB und
JJJG JJJG
JJJG
AC aufgespannt wird, A P = AB × AC . Für den Flächeninhalt gilt
JJJG JJJG
A P = 2A und somit A = 1 AB × AC .
2
211
263
4. Das Volumen des Spats berechnet sich nach Grundseite mal Höhe:
V = G ⋅ h.
G G
Hierbei ist die Grundseite ein Parallelogramm, für das G = a × b gilt.
G
G
Für die Höhe h gilt h = c ⋅ cos α , wobei α der Winkel zwischen c und
G
G
einem auf a und b senkrecht stehenden Vektor ist.
G G G
⇒ V = a × b ⋅ c ⋅ cos α
G G G
Nach Satz 5 (S. 256) ist dies V = ( a × b ) ∗ c .
5. Das Volumen einer Pyramide berechnet sich nach Grundseite mal Höhe
geteilt durch 3: V = 1 G ⋅ h.
3
G G
Die Grundseite ist die Hälfte eines Parallelogramms: G = 1 ( a × b ) .
2
G
G
Für die Höhe gilt h = c ⋅ cos α , wobei α der Winkel zwischen c und
G
G
einem auf a und b senkrecht stehenden Vektor ist.
G G G
⇒ V = 1 ⋅ 1 a × b ⋅ c ⋅ cos α
3 2
G G G
Nach Satz 5 (S. 256) ist dies V = 1 ( a × b ) ∗ c .
6
13
G G ⎛ ⎞
G
G
6. Zu u und v orthogonale Vektoren sind Vielfache von u × v = ⎜ −9 ⎟ .
⎜ −3 ⎟
⎝ ⎠
−1
G G ⎛ ⎞
7. a) a × b = ⎜ 17 ⎟
⎜ 10 ⎟
⎝ ⎠
16
G G ⎛ ⎞
b) a × b = ⎜ 6 ⎟
⎜ 15 ⎟
⎝ ⎠
−4
G G ⎛ ⎞
c) a × b = ⎜ −7 ⎟
⎜ 1⎟
⎝ ⎠
⎛ 5⎞ ⎛9⎞
⎛ 26 ⎞
JJJG JJJG
8. a) A = 1 PQ × PR = 1 ⎜ −6 ⎟ × ⎜ 7 ⎟ = 1 ⎜ 81 ⎟ = 1 15 158 ≈ 61,56
2
2 ⎜
⎟ ⎜ ⎟ 2 ⎜ 89 ⎟ 2
⎝ 4 ⎠ ⎝ −9 ⎠
⎝ ⎠
⎛ 4 ⎞ ⎛3⎞
⎛ 147 ⎞
JJJG JJJG
b) A = 1 PQ × PR = 1 ⎜ 7 ⎟ × ⎜ 12 ⎟ = 1 ⎜ −57 ⎟ = 1 3 2 843 ≈ 80, 00
2
2 ⎜
2
⎟ ⎜ ⎟ 2 ⎜ 27 ⎟
⎝ −7 ⎠ ⎝ 9 ⎠
⎝
⎠
212
263
9. Berechne das Volumen der Pyramide.
Die Punkte bilden eine Pyramide ⇔ V > 0.
Volumen (mit Aufgabe 5):
JJJG JJJG JJJG
V = 1 ⋅ ( AB × AC ) ∗ AD = 217 ≈ 36,167
6
6
Oberflächeninhalt = Summe über 4 Dreiecke, z. B.
⎛ −6 ⎞
JJJG JJJG
A1 = 1 AB × AC = 1 ⎜ 9 ⎟ = 1 217 ≈ 7,365
2
2 ⎜
⎟ 2
⎝ −10 ⎠
A2 =
1
2
JJJG JJJG
AB × AD =
1
2
⎛ 14 ⎞
⎜ −21 ⎟ = 7 62 ≈ 27,559
⎜ −49 ⎟ 2
⎝
⎠
A3 =
1
2
JJJG JJJG
AC × AD =
1
2
⎛ −27 ⎞
⎜ −68 ⎟ = 1 7378 ≈ 42,948
⎜ −45 ⎟ 2
⎝
⎠
⎛ 2⎞ ⎛ 8 ⎞
⎛ −47 ⎞
⎜ −2 ⎟ x ⎜ −11⎟ = 1 ⎜ −38 ⎟ = 1 3689 ≈ 30,369
⎜ −3 ⎟ ⎜ 7 ⎟ 2 ⎜ −6 ⎟ 2
⎝ ⎠ ⎝
⎠
⎝
⎠
⇒ A = A1 + A 2 + A 3 + A 4 = 108, 241
A4 =
1
2
JJJG JJJG
BC × BD =
1
2
JJJG JJJG ⎛ 4 ⎞
JJJG JJJG ⎛ −1⎞
JJJG JJJG
10. a) Da AB = DC = ⎜ 3 ⎟ und AD = BC = ⎜ 2 ⎟ und AB ⋅ AD = 0 ist,
⎜ −1 ⎟
⎜2⎟
⎝ ⎠
⎝ ⎠
ist die Grundfläche ein Rechteck.
b) Es gibt 3 Flächen:
⎛ 8⎞
JJJG JJJG
A ABCD = AB × AD = ⎜ −7 ⎟ = 3 26 ≈ 15,3
⎜ 11 ⎟
⎝ ⎠
⎛ −1⎞ ⎛ −2 ⎞
⎛8⎞
JJJG JJJG
A BCFG = BC × BF = ⎜ 2 ⎟ × ⎜ 2 ⎟ = ⎜ 2 ⎟ = 6 2 ≈ 8,5
⎜2⎟ ⎜ 6⎟
⎜ 2⎟
⎝ ⎠ ⎝ ⎠
⎝ ⎠
⎛ −20 ⎞
JJJG JJJG
A ABEF = BA × BF = ⎜ 22 ⎟ = 6 30 ≈ 32,9
⎜ −14 ⎟
⎝
⎠
⇒ Die Seiten ABEF und DCGH haben den größten Flächeninhalt.
⎛ −8 ⎞ ⎛ −2 ⎞
JJJG JJJG JJJG
c) V = ( BA × BC ) ∗ BF = ⎜ 7 ⎟ ⋅ ⎜ 2 ⎟ = 36
⎜ −11⎟ ⎜ 6 ⎟
⎝
⎠ ⎝ ⎠
213
263
11. a) R(2 | 10 | 10)
b) Fehler in der 1. Auflage: Punkte P, Q, R, S liegen nicht in einer Ebene.
Korrektur: Setze S(5 | 0 | 10).
Zerlege das Viereck in zwei Dreiecke PSQ und RSQ
A = A PSQ + A RSQ
JJG JJJG
JJJG JJJG
= 1 PS × PQ + 1 RS × RQ
2
=
1
2
2
⎛ −5 ⎞ ⎛ 0 ⎞
⎜ 0 ⎟ × ⎜ 10 ⎟ +
⎜ 5 ⎟ ⎜ −3 ⎟
⎝ ⎠ ⎝ ⎠
1
2
⎛ 3 ⎞ ⎛8⎞
⎜ −10 ⎟ × ⎜ 0 ⎟
⎜ 0 ⎟ ⎜ −8 ⎟
⎝
⎠ ⎝ ⎠
⎛ −50 ⎞
⎛ 80 ⎞
⎜ −15 ⎟ + 1 ⎜ 24 ⎟ = 13 209 = 93,97
2
⎜ −50 ⎟ 2 ⎜ 80 ⎟
⎝
⎠
⎝ ⎠
Bei S: α S = 101, 723°
c) Bei P: α P = 101, 723°
=
1
2
Bei R: α R = 78, 277°
Bei Q: α Q = 78, 277°
−1
⎛ 0 ⎞
⎛6⎞
G ⎛ ⎞
12. a) Es gilt E t : x = ⎜ 1 ⎟ + r ⎜ 1 ⎟ + s ⎜ 3t ⎟
⎜ −1⎟
⎜ 2t + 2 ⎟
⎜0⎟
⎝ ⎠
⎝
⎠
⎝ ⎠
7
3t(2
2t)
−
+
⎞
⎛
⎞
G ⎛
und g t : x = ⎜ −11⎟ + r ⎜ 6(2 + 2t) ⎟
⎜ 4 ⎟
⎜
⎟
−6
⎝
⎠
⎝
⎠
g t kann wegen der x 3 -Koordinate −6 nur parallel zur x 3 -Achse
laufen. 2 + 2t = 0 ⇔ t = −1.
⎛ 0⎞
JJJJJJG JJJJJJG
b) A = 1 AB −1 × AC −1 = 1 ⎜ 0 ⎟ = 3
2
2 ⎜
⎟
⎝ −6 ⎠
Lernfeld
Ebenen − Ungekrümmtes im Raum
264
1. •
•
•
•
•
•
4 Punkte
2 Geraden, die senkrecht aufeinander stehen
2 Geraden, die echt parallel sind
2 Geraden
1 Gerade und 1 Punkt
3 Punkte
214
265
⎛1⎞
JJJG ⎛ 0 ⎞
G JJJG
g AB : x = OA + t ⋅ AB = ⎜ 3 ⎟ + t ⋅ ⎜ 0 ⎟ ; t ∈ \
⎜0⎟
⎜0⎟
⎝ ⎠
⎝ ⎠
⎛0⎞
JJJG ⎛ 0 ⎞
G JJJG
g AC : x = OA + s ⋅ AC = ⎜ 3 ⎟ + s ⋅ ⎜ 0 ⎟ ; s ∈ \
⎜0⎟
⎜ 2⎟
⎝ ⎠
⎝ ⎠
Verschobene Geraden AB entlang AC
0
0
⎛1⎞ ⎛ 0⎞
⎛1⎞
G ⎛ ⎞ ⎛ ⎞
g A ′B′ : x = ⎜ 3 ⎟ + ⎜ 0 ⎟ + t ⋅ ⎜ 0 ⎟ = ⎜ 3 ⎟ + t ⋅ ⎜ 0 ⎟
⎜0⎟ ⎜ 2⎟
⎜ 0⎟ ⎜ 2⎟
⎜ 0⎟
⎝ ⎠ ⎝ ⎠
⎝ ⎠ ⎝ ⎠
⎝ ⎠
0
⎛0⎞
⎛1⎞ ⎛ 0⎞
⎛1⎞
G ⎛ ⎞
g A ′′B′′ : x = ⎜ 3 ⎟ + 2 ⎜ 0 ⎟ + t ⋅ ⎜ 0 ⎟ = ⎜ 3 ⎟ + t ⋅ ⎜ 0 ⎟
⎜0⎟
⎜ 2⎟
⎜ 0⎟ ⎜ 4⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠ ⎝ ⎠
⎝ ⎠
Allgemein kann man die verschobenen Geraden durch die folgende
Gleichung angeben:
0
⎛ 0⎞
⎛1⎞
G ⎛ ⎞
g AB verschoben : x = ⎜ 3 ⎟ + s ⎜ 0 ⎟ + t ⋅ ⎜ 0 ⎟ , s, t ∈ \
⎜0⎟
⎜ 2⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
Indem man zunächst entlang AB ein gewisses Stück und dann in
Richtung AC ein anderes Stück geht, erreicht man jeden Punkt der
Ebene, in der die Glasfläche ABCD liegt.
Also ist durch
0
⎛0⎞
⎛1⎞
G ⎛ ⎞
x = ⎜ 3 ⎟ + s ⎜ 0 ⎟ + t ⋅ ⎜ 0 ⎟ jeder Punkt der Ebene, also die Ebene
⎜0⎟
⎜ 2⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
gegeben.
0
⎛0⎞
G ⎛ ⎞
• z. B. g CE : x = ⎜ 3 ⎟ + t ⋅ ⎜ −3 ⎟ ; t ∈ \
⎜ 2⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
0
⎛1⎞
G ⎛ ⎞
g CD : x = ⎜ 3 ⎟ + s ⋅ ⎜ 0 ⎟ ; s ∈ \
⎜ 2⎟
⎜0⎟
⎝ ⎠
⎝ ⎠
0
1
⎛
⎞
⎛
⎞
⎛0⎞
JJJG
⇒ OP′ = ⎜ 3 ⎟ + s ⋅ ⎜ 0 ⎟ + t ⋅ ⎜ −3 ⎟ ; s, t ∈ \
⎜ 2⎟
⎜0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
2. •
215
265
3. Die Ebenen eines „Pultdaches“ schneiden sich.
In der Reihe der Häuser sind jeweils die Ebenen der äquivalenten Dachhälften parallel und schneiden sich nicht.
Es gibt nur 3 verschiedene Lagebeziehungen von Ebenen: Schnitt in einer
Geraden, echte Parallelität und Identität.
4. a) Der Winkel α ist der kleinste
Winkel zwischen Gerade und
Ebene. Dieser ergibt sich, wenn
er in einer orthogonalen Ebene
zu der Dachfläche gemessen
wird.
b) Reflexionsgesetz:
Einfallwinkel β = Reflexionswinkel β
Da Einfallwinkel = Reflexionswinkel
gilt, kann man aus den Positionen
des Senders, des Empfängers und des
Spiegels mithilfe der Trigonometrie
die Winkel bestimmen.
In der Abbildung ist tan β =
bzw. α = 90° − β − tan −1
( ha )
a
h
216
4.4 Ebenen im Raum
4.4.1 Parameterdarstellung einer Ebene
268
JJJG
JJJG
JJJG
2. Maren: Stützvektor: OA ; Richtungsvektoren: AB und AC
JJJG
JJJG
JJJG
Janik: Stützvektor: OB ; Richtungsvektoren: − 1 AB und BC
2
weitere Beispiele
7
⎛ −5 ⎞ ⎛ 2 ⎞
G ⎛ ⎞
E: x = ⎜ 0 ⎟ + s ⎜ 3 ⎟ + t ⎜ −1 ⎟
⎜ −7 ⎟
⎜ 5 ⎟ ⎜ −4 ⎟
⎝ ⎠
⎝ ⎠ ⎝ ⎠
2
⎛ −9 ⎞ ⎛ −8 ⎞
G ⎛ ⎞
E: x = ⎜ 3 ⎟ + s ⎜ 5 ⎟ + t ⎜ 4 ⎟
⎜ −2 ⎟
⎜ 13 ⎟ ⎜ 16 ⎟
⎝ ⎠
⎝ ⎠ ⎝ ⎠
JJJG JJJG
G
G
3. a) OB = OA + 1 ⋅ u + 1,5 ⋅ v
JJJG JJJG
G
G
OC = OA + 1,5 ⋅ u − 0,5 ⋅ v
JJJG JJJG
G
G
OD = OA − 1 ⋅ u + 1,5 ⋅ v
JJJG JJJG
G
G
b) OX = OA + s ⋅ u + t ⋅ v mit s, t ∈ \
G
Man geht zunächst ein Vielfaches s von u und danach ein Vielfaches r
G
von v und erreicht somit jeden beliebigen Punkt X.
⎛3⎞
⎛ −1 ⎞ ⎛ 3 ⎞
G
4. a) Z. B: E: x = ⎜ −5 ⎟ + s ⎜ 6 ⎟ + t ⎜ −0, 5 ⎟ ; s, t ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜
⎟⎟
⎝ 10 ⎠
⎝ 2 ⎠ ⎝ 12 ⎠
b) Für obiges Beispiel:
⎛ 10 ⎞
⎛ 43 ⎞
⎛ −4,8 ⎞
(1) ⎜ 5, 5 ⎟
(2) ⎜ −35 ⎟
(3) ⎜ −0, 2 ⎟
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎝ 50 ⎠
⎝ 146 ⎠
⎝ 17, 6 ⎠
⎛ 1, 675 ⎞
(4) ⎜ −3, 6125 ⎟
⎜⎜
⎟⎟
⎝ 5, 9 ⎠
5. Beispiele:
⎛0⎞
⎛ 2⎞
⎛ 4⎞
JJJG
JJJG ⎜ ⎟
G JJJG
⎜ ⎟
⎜ ⎟
a) E: x = OP + λ PQ + μ PR = ⎜ 1 ⎟ + λ ⋅ ⎜ −1 ⎟ + μ ⋅ ⎜ 7 ⎟ ; λ, μ ∈ \
⎜2⎟
⎜ 2⎟
⎜ −2 ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎛ 1⎞
⎛ 1⎞
⎛ 9⎞
G ⎜ ⎟
⎜ ⎟
⎜ ⎟
b) E: x = ⎜ 1⎟ + λ ⋅ ⎜ 1 ⎟ + μ ⋅ ⎜ 3 ⎟ ; λ, μ ∈ \
⎜ 1⎟
⎜2⎟
⎜ 5⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
217
268
⎛1 ⎞
⎛2⎞
⎛2⎞
G ⎜ ⎟
⎜ ⎟
⎜ ⎟
5. c) E: x = ⎜ −2 ⎟ + s ⋅ ⎜ 6 ⎟ + t ⋅ ⎜ 6 ⎟ ; s, t ∈ \
⎜ 3⎟
⎜ −5 ⎟
⎜2⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎛0⎞
⎛ -10 ⎞
⎛ −4 ⎞
G ⎜ ⎟
⎜
⎟
⎜
⎟
d) E: x = ⎜ 7 ⎟ + s ⋅ ⎜ −7 ⎟ + t ⋅ ⎜ −11 ⎟ ; s, t ∈ \
⎜2⎟
⎜ −8 ⎟
⎜ −2 ⎟
⎝ ⎠
⎝
⎠
⎝
⎠
269
6. Zunächst Probe, dass P nicht auf g liegt (Punktprobe).
⎛4⎞
⎛ 3⎞
⎛ 1− 4 ⎞ ⎛ 4⎞
⎛ 3⎞
⎛ −3 ⎞
G ⎜ ⎟
⎜ ⎟
⎜
⎟ ⎜ ⎟
⎜ ⎟
⎜ ⎟
a) E: x = ⎜ 0 ⎟ + s ⋅ ⎜ −1 ⎟ + t ⋅ ⎜ 4 − 0 ⎟ = ⎜ 0 ⎟ + s ⋅ ⎜ −1 ⎟ + t ⋅ ⎜ 4 ⎟ ; s, t ∈ \
⎜2⎟
⎜ −3 ⎟
⎜ −1 − 2 ⎟ ⎜ 2 ⎟
⎜ −3 ⎟
⎜ −3 ⎟
⎝ ⎠
⎝ ⎠
⎝
⎠ ⎝ ⎠
⎝ ⎠
⎝ ⎠
⎛1⎞
⎛ 5⎞
⎛ 1⎞
G ⎜ ⎟
⎜ ⎟
⎜ ⎟
b) E: x = ⎜ 0 ⎟ + s ⋅ ⎜ 2 ⎟ + t ⋅ ⎜ 4 ⎟ ; s, t ∈ \
⎜0⎟
⎜ −3 ⎟
⎜ −3 ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎛ −200 ⎞
⎛ 10 ⎞
⎛ 200 ⎞
G ⎜
⎟
⎜
⎟
⎜
⎟
c) E: x = ⎜ 150 ⎟ + t ⋅ ⎜ −10 ⎟ + s ⋅ ⎜ −150 ⎟ ; s, t ∈ \
⎜ 30 ⎟
⎜ 5 ⎟
⎜ −30 ⎟
⎝
⎠
⎝
⎠
⎝
⎠
7. Gleichsetzen ergibt das Gleichungssystem
−s − 2t = 1
2s − t = −2
s + t = −1
welches die eindeutige Lösung s = −1; t = 0 besitzt.
Schnittpunkt: S(−2 | 0 | −2)
⎛ −2 ⎞
⎛ −1 ⎞
⎛2⎞
G ⎜ ⎟
⎜ ⎟
⎜ ⎟
E: x = ⎜ 0 ⎟ + s ⋅ ⎜ 2 ⎟ + t ⋅ ⎜ 1 ⎟ ; s, t ∈ \
⎜ −2 ⎟
⎜1⎟
⎜ −1 ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎛ 5⎞
⎛ 3⎞
⎛ 0 − 5⎞ ⎛ 5⎞
⎛ 3⎞
⎛ −5 ⎞
G ⎜ ⎟
⎜ ⎟
⎜
⎟ ⎜ ⎟
⎜ ⎟
⎜ ⎟
8. a) E: x = ⎜ 0 ⎟ + s ⋅ ⎜ −1 ⎟ + t ⋅ ⎜ −1 − 0 ⎟ = ⎜ 0 ⎟ + s ⋅ ⎜ −1 ⎟ + t ⋅ ⎜ −1 ⎟ ; s, t ∈ \
⎜2⎟
⎜ 4⎟
⎜ −1 − 2 ⎟ ⎜ 2 ⎟
⎜ 4⎟
⎜ −3 ⎟
⎝ ⎠
⎝ ⎠
⎝
⎠ ⎝ ⎠
⎝ ⎠
⎝ ⎠
b) Die Richtungsvektoren sind parallel zueinander:
⎛ 1 ⎞ ⎛ −3 ⎞
⎛2⎞
⎛ 1⎞
⎛ 1⎞
G ⎜ ⎟
⎜ ⎟ ⎜ ⎟
⎜ ⎟
⎜ ⎟
(−3) ⋅ ⎜ 1 ⎟ = ⎜ −3 ⎟ , daher E: x = ⎜ 1 ⎟ + s ⋅ ⎜ 1 ⎟ + t ⋅ ⎜ −5 ⎟ ; s, t ∈ \
⎜ −2 ⎟ ⎜ 6 ⎟
⎜3⎟
⎜ −2 ⎟
⎜ −2 ⎟
⎝ ⎠ ⎝ ⎠
⎝ ⎠
⎝ ⎠
⎝ ⎠
218
269
9. Aufgrund der selbstständigen Wahl des Koordinatensystems gibt es
unendlich viele Lösungsmöglichkeiten.
Beispiel: Wahl des Ursprungs in dem Mittelpunkt der Grundfläche.
Koordinatensystem: Standard-Rechtssystem
⎛0⎞
⎛1⎞ ⎛0⎞
G
Grundfläche: E G : x = ⎜ 0 ⎟ + s ⎜ 0 ⎟ + t ⎜ 1 ⎟ ; s, t ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝0⎠
⎝0⎠ ⎝0⎠
⎛0⎞
⎛1⎞ ⎛ 0 ⎞
G
Seitenflächen: E S1 : x = ⎜ 0 ⎟ + s ⎜ 0 ⎟ + t ⎜ 2, 5 ⎟ ; s, t ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜
⎟⎟
⎝ 12 ⎠
⎝ 0 ⎠ ⎝ 12 ⎠
⎛0⎞
⎛ 0 ⎞ ⎛ 2, 5 ⎞
G
E S2 : x = ⎜ 0 ⎟ + s ⎜ 1 ⎟ + t ⎜ 0 ⎟ ; s, t ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜
⎟⎟
⎝ 12 ⎠
⎝ 0 ⎠ ⎝ 12 ⎠
Seitenfläche
⎛0⎞
⎛ −1 ⎞ ⎛ 0 ⎞
G
E S3 : x = ⎜ 0 ⎟ + s ⎜ 0 ⎟ + t ⎜ −2, 5 ⎟ ; s, t ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜
⎟⎟
⎝ 12 ⎠
⎝ 0 ⎠ ⎝ 12 ⎠
⎛0⎞
⎛ 0 ⎞ ⎛ −2, 5 ⎞
G
E S 4 : x = ⎜ 0 ⎟ + s ⎜ −1 ⎟ + t ⎜ 0 ⎟ ; s, t ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜
⎟⎟
⎝ 12 ⎠
⎝ 0 ⎠ ⎝ 12 ⎠
10. Zum Beispiel:
P1: s = 0, t = 0: P1 (−2; 0; 1);
P2 : s = 1, t = 2: P2 (−3; 5; 2);
P3 : s = −1, t = 1: P3 (−4; 1; 0)
⎛ −2 ⎞
⎛ −1 ⎞
⎛ −2 ⎞
G
E: x = ⎜ 0 ⎟ + s ⋅ ⎜ 5 ⎟ + t ⋅ ⎜ 1 ⎟ ; s, t ∈ \
⎜ 1⎟
⎜ 1⎟
⎜ −1 ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
11. Sie hat nicht überprüft, ob die 3 Punkte auf einer Geraden liegen. Da A, B,
⎛ 3⎞
⎛ 9⎞
C auf einer Geraden liegen, sind die Richtungsvektoren ⎜ 3 ⎟ und ⎜ 9 ⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ −2 ⎠
⎝ −6 ⎠
linear abhängig und es wird keine Ebene sondern eine Gerade beschrieben.
12. Kein Punkt liegt auf der Ebene.
270
⎛6⎞
⎛ 0⎞
⎛ −6 ⎞
⎛0⎞
⎛ 6⎞
⎛ 1⎞
G ⎜ ⎟
G ⎜ ⎟
⎜
⎟
⎜
⎟
⎜
⎟
13. a) E : x = 5 + λ ⋅ −5 + μ ⋅ −4 b) E : x = 3 + λ ⋅ −1 + μ ⋅ ⎜ 3 ⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝3⎠
⎝ −1 ⎠
⎝ −2 ⎠
⎝0⎠
⎝ 2⎠
⎝ 3⎠
219
270
14. Dadurch, dass Timo die Konstanten in die 1. Spalte der Matrix geschrieben
hat, lautet das lineare Gleichungssystem nach Einsatz des GTR:
1 = 0, 5t
0 = s + 0, 5t .
0=0
Man kann also nicht direkt die Werte von s, t ablesen, sondern muss noch
rechnen: t = 2 und s = −1
15. a) s = 0, t = 1
b) s = 2, t = −1
c) P liegt nicht in E
d) s = −1, t = − 14
16. Geprüft wird, ob P4 in der Ebene E liegt, die von P1 , P2 , P3 bestimmt ist.
s = 21
⎛ 3⎞ ⎛ 7⎞
⎛ −8 ⎞
⎛ −7 ⎞
⎜ ⎟ ⎜ ⎟
⎜ ⎟
⎜ ⎟
a) ⎜ 2 ⎟ = ⎜ 2 ⎟ + s ⋅ ⎜ 0 ⎟ + t ⋅ ⎜ −4 ⎟ ⇔ t = 0 , d. h. P4 ∈ E
⎜ 1 ⎟ ⎜ −1 ⎟
⎜ 4⎟
⎜ 3⎟
s = 21
⎝ ⎠ ⎝ ⎠
⎝ ⎠
⎝ ⎠
s=0
⎛ −2 ⎞ ⎛ 2 ⎞
⎛ −4 ⎞
⎛ −2 ⎞
⎜ ⎟ ⎜ ⎟
⎜ ⎟
⎜ ⎟
b) ⎜ −1 ⎟ = ⎜ 1 ⎟ + s ⋅ ⎜ 1 ⎟ + t ⋅ ⎜ −1 ⎟ ⇔ t = 2 , d. h. P4 ∈ E
⎜ 5⎟ ⎜ 3⎟
⎜ −2 ⎟
⎜ 1⎟
s=0
⎝ ⎠ ⎝ ⎠
⎝ ⎠
⎝ ⎠
s = −1
⎛ 7 ⎞ ⎛ 5⎞
⎛ −4 ⎞
⎛ − 2⎞
⎜ ⎟ ⎜ ⎟
⎜ ⎟
⎜
⎟
c) ⎜ 0 ⎟ = ⎜ −1⎟ + s ⋅ ⎜ 2 ⎟ + t ⋅ ⎜ 3 ⎟ ⇔ t = 1 , d. h. P4 ∉ E
⎜ −1 ⎟ ⎜ 5 ⎟
⎜ −6 ⎟
⎜ −10 ⎟
−1 = 1
⎝ ⎠ ⎝ ⎠
⎝ ⎠
⎝
⎠
17. a) Überprüfe, ob P, Q und R nicht auf einer Geraden liegen.
JJJG JJJG
(1) PQ = QR (d. h. die Punkte liegen auf einer Geraden)
JJJG
JJJG
(2) PR = 2 ⋅ PQ (d. h. die Punkte liegen auf einer Geraden)
b) Überprüfe, ob P nicht auf g liegt.
(1) Ja, denn P liegt nicht auf g.
G JJJG
(2) Für s = 10 ergibt sich x = OP . P liegt auf g.
c) Überprüfe, ob die Geraden nicht windschief zueinander oder identisch
sind.
s = − 61
3s + t = −1
⎛2⎞
⎛ 3⎞ ⎛ 1⎞
⎛ −1 ⎞
⎜ ⎟
⎜ ⎟ ⎜ ⎟
⎜ ⎟
(1) ⎜ 1 ⎟ + s ⋅ ⎜ 0 ⎟ = ⎜ 2 ⎟ + t ⋅ ⎜ 2 ⎟ ⇔ − 2t = +1 ⇔ t = −0,5
⎜ 4⎟
⎜ 1 ⎟ ⎜ 3⎟
⎜ 1⎟
s − t = −1
s = −0,5
⎝ ⎠
⎝ ⎠ ⎝ ⎠
⎝ ⎠
Die Geraden sind windschief zueinander.
−s =1
s = −1
⎛ 1⎞
⎛ −1 ⎞ ⎛ 2 ⎞
⎛0⎞
⎜ ⎟
⎜ ⎟ ⎜ ⎟
⎜ ⎟
(2) ⎜ 1 ⎟ + s ⋅ ⎜ 1 ⎟ = ⎜ 1 ⎟ + t ⋅ ⎜ 1 ⎟ ⇔ s − t = 0 ⇔ t = −1
⎜0⎟
⎜ 2⎟ ⎜ 1⎟
⎜ 1⎟
2s − t = 1
t = −3
⎝ ⎠
⎝ ⎠ ⎝ ⎠
⎝ ⎠
Die Geraden sind windschief zueinander.
220
270
3s − 6t = −6
⎛ 5⎞
⎛ 3 ⎞ ⎛ −1 ⎞
⎛ 6⎞
t beliebig und
⎜ ⎟
⎜ ⎟ ⎜ ⎟
⎜ ⎟
17. c) (3) ⎜ 0 ⎟ + s ⋅ ⎜ −1 ⎟ = ⎜ 2 ⎟ + t ⋅ ⎜ −2 ⎟ ⇔ −s + 2t = 2 ⇔
s = 2t − 2
⎜2⎟
⎜ 4 ⎟ ⎜ −6 ⎟
⎜ 8⎟
4s − 8t = −8
⎝ ⎠
⎝ ⎠ ⎝ ⎠
⎝ ⎠
Die beiden Geraden sind identisch.
⎛2⎞
⎛ 4⎞
⎛ 2⎞
(4) Da ⎜ −1⎟ ⋅ 2 = ⎜ −2 ⎟ und ⎜ 3 ⎟ ∉ g1
⎜3⎟
⎜ 0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
sind die Geraden parallel und nicht identisch.
271
18. a) Die 3 Stützvektoren sind identisch
⇒ Ebene und Geraden haben gemeinsamen Punkt.
Jeweils der Richtungsvektor der Geraden ist auch ein Richtungsvektor
der Ebene.
b) Beispielhaftes Vorgehen:
3
⎛1⎞
G ⎛ ⎞
G
• F enthält g1 ⇒ F: x = ⎜ 1 ⎟ + s ⎜ −1⎟ + t ⋅ u
⎜ 2⎟
⎜2⎟
⎝ ⎠
⎝ ⎠
3
G ⎛ ⎞ JJJG
• Mit P nicht in E ist z. B. u = ⎜ 1 ⎟ − OP.
⎜ 2⎟
⎝ ⎠
2
G ⎛ ⎞
Beispiel: P(1 | 1 | 1) ⇒ u = ⎜ 0 ⎟
⎜1⎟
⎝ ⎠
3⎞
1 ⎞ ⎛ 2⎞
⎛
⎛
G
⇒ z. B. F: x = ⎜ 1 ⎟ + s ⎜ −1⎟ + t ⎜ 0 ⎟
⎜ 2⎟
⎜ 2 ⎟ ⎜1⎟
⎝ ⎠
⎝ ⎠ ⎝ ⎠
221
271
18. c) Beispielhaftes Vorgehen:
⎛ 1 ⎞ ⎛ 2⎞
G G
• G parallel zu E ⇒ G: x = a + s ⎜ −1⎟ + t ⎜ 1 ⎟
⎜ 2 ⎟ ⎜ 4⎟
⎝ ⎠ ⎝ ⎠
JJJ
G
G
• G enthält P ⇒ a = OP
1
⎛ 1 ⎞ ⎛ 2⎞
G ⎛ ⎞
Beispiel mit P(1 | 1 | 1): G: x = ⎜ 1⎟ + s ⎜ −1⎟ + t ⎜ 1 ⎟
⎜ 1⎟
⎜ 2 ⎟ ⎜ 4⎟
⎝ ⎠
⎝ ⎠ ⎝ ⎠
⎛ 1⎞
⎛0⎞
G
19. a) x = s ⋅ ⎜ 0 ⎟ + t ⋅ ⎜ 1⎟
⎜0⎟
⎜0⎟
⎝ ⎠
⎝ ⎠
⎛0⎞
⎛0⎞
G
b) x = s ⋅ ⎜ 1⎟ + t ⋅ ⎜ 0 ⎟
⎜0⎟
⎜ 1⎟
⎝ ⎠
⎝ ⎠
⎛ 3⎞
⎛ 1⎞
⎛0⎞
G
c) x = ⎜ 1⎟ + s ⋅ ⎜ 0 ⎟ + t ⋅ ⎜ 0 ⎟
⎜ −2 ⎟
⎜0⎟
⎜ 1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎛0⎞
⎛ 1⎞
⎛0⎞
G
d) x = ⎜ 0 ⎟ + s ⋅ ⎜ 0 ⎟ + t ⋅ ⎜ 1⎟
⎜ 2⎟
⎜0⎟
⎜0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎛ 3⎞
⎛ −3 ⎞
⎛ −3 ⎞
G
e) x = ⎜ 0 ⎟ + s ⋅ ⎜ 1⎟ + t ⋅ ⎜ 0 ⎟
⎜0⎟
⎜ 0⎟
⎜ −1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎛0⎞
⎛ 3⎞
⎛ 0⎞
G
f) x = ⎜ 0 ⎟ + s ⋅ ⎜ 0 ⎟ + t ⋅ ⎜ −2 ⎟
⎜ 4⎟
⎜ −4 ⎟
⎜ −4 ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎛ 1⎞
⎛0⎞
G
g) x = s ⋅ ⎜ 2 ⎟ + t ⋅ ⎜ 0 ⎟
⎜0⎟
⎜ 1⎟
⎝ ⎠
⎝ ⎠
20. - 3 Punkte: Beispiel: Schülerband S. 268, Aufgabe 5.
- 1 Punkt und 1 Gerade: Beispiel: Schülerband S. 269, Aufgabe 6
- 2 Geraden, die sich in einem Punkt schneiden:
Beispiel: Schülerband S. 269, Aufgabe 7
- 2 verschiedene parallele Geraden: Beispiel: Schülerband S. 269,
Aufgabe 8
⎛4⎞
⎛ 0⎞
⎛ −4 ⎞
G ⎜ ⎟
⎜
⎟
21. a) E : x = 4 + λ ⋅ −2 + μ ⋅ ⎜ 0 ⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝2⎠
⎝ 2⎠
⎝ 2⎠
b) Es muss gelten: λ, μ ≥ 0 und λ + μ ≤ 1.
22. a) Der Stützvektor aller drei Parameterdarstellungen ist gleich. Die
Richtungsvektoren der Ebene sind die Richtungsvektoren der beiden
Geraden. Für s = 0, r beliebig ergibt sich aus der Ebene die Gerade g1
und für r = 0 und s beliebig die Gerade g 2 .
222
271
G G
G
G
22. b) Setze in x = a + r ⋅ u + s ⋅ v
G G
G
(1) s = 0, das ergibt g: x = a + t ⋅ u
G G
G
(2) r = 0, das ergibt g: x = a + t ⋅ v
G G G
G
(3) r = 1, das ergibt g: x = a + u + t ⋅ v
G G
G
G
(4) s = 3, das ergibt g: x = a + 3v + t ⋅ u
4.4.2 Lagebeziehungen zwischen Gerade und Ebene
273
3. a) (1) Gleichsetzen führt auf Gleichungssystem:
r−t =1
r+t =1
2r − 3s + 4t = −1 ⇒ 6t − 3s = −3
0=0
− 4r + 2s = −2
Das Gleichungssystem hat einen freien Parameter und somit
unendlich viele Lösungen ⇒ g liegt in E.
(2) Richtungsvektor von g liegt in E (Linearkombination der Richtungs⎛1⎞ ⎛1⎞
⎛0⎞
vektoren von E): ⎜ −4 ⎟ = ⎜ 2 ⎟ + 2 ⎜ −3 ⎟ .
⎜ 0 ⎟ ⎜ −4 ⎟
⎜2⎟
⎝ ⎠ ⎝ ⎠
⎝ ⎠
JJJG
Punkt A(2 | 1 | −1) des Stützvektors OA von g liegt in E für r = 1;
s = 1.
b) Beispiele:
1
1
G ⎛ ⎞ ⎛ ⎞
g1: x = ⎜ 2 ⎟ + t ⎜ 2 ⎟ mit t ∈ \
⎜ 1 ⎟ ⎜ −4 ⎟
⎝ ⎠ ⎝ ⎠
1
0
G ⎛ ⎞ ⎛ ⎞
g 2 : x = ⎜ 2 ⎟ + t ⎜ −3 ⎟ mit t ∈ \
⎜1⎟ ⎜ 2 ⎟
⎝ ⎠ ⎝ ⎠
2
1
G ⎛ ⎞ ⎛ ⎞
g 3 : x = ⎜ 4 ⎟ + t ⎜ −1 ⎟ mit t ∈ \
⎜ −3 ⎟ ⎜ −2 ⎟
⎝ ⎠ ⎝ ⎠
274
4. Parameterdarstellung der Trägergeraden des Seils
⎛1⎞
JJJG ⎛ 8 ⎞
OX = ⎜ 11 ⎟ + r ⎜ 3 ⎟ ; r ∈ \
⎜ 21⎟
⎜ 4⎟
⎝ ⎠
⎝ ⎠
JJJG ⎛ 8 + r ⎞
Ortsvektor des Schnittpunkts: OS = ⎜ 11 + 3r ⎟ .
⎜ 21 + 4r ⎟
⎝
⎠
Dieser Ortsvektor muss auch die Ebenengleichung erfüllen. Einsetzen
liefert r = −4; t = −2; s = 0. Aus der Parameterdarstellung der Geraden folgt
S(4 | −1 | 5). Dies ist ungefähr der Punkt, an dem die Verankerung
angebracht werden sollte.
223
274
(3) keine Lösung, g & E
5. a) (1) S(−3 | 8 | 1)
(2) keine Lösung, g & E
(4) g liegt in E
b) g und E haben den gleichen Stützvektor.
Richtungsvektor von g ist auch Richtungsvektor von E.
6. (1) Gerade und Ebene sind parallel, sie haben keinen Schnittpunkt.
(2) Gerade liegt in der Ebene.
(3) Gerade und Ebene schneiden sich in einem Punkt.
⎛ −1 ⎞
⎛ 12 ⎞
G ⎜ ⎟
⎜ ⎟
7. a) Z. B.: g: x = ⎜ 2 ⎟ + t ⋅ ⎜ 13 ⎟ ; t ∈ \
⎜3⎟
⎜2⎟
⎝ ⎠
⎝ ⎠
⎛ −1 ⎞
⎛ 3⎞
G ⎜ ⎟
⎜ ⎟
b) Z. B.: g: x = ⎜ 2 ⎟ + t ⋅ ⎜ −2 ⎟ ; t ∈ \
⎜3⎟
⎜ 1⎟
⎝ ⎠
⎝ ⎠
⎛ −1 ⎞
⎛ 2⎞
G ⎜ ⎟
⎜ ⎟
oder g: x = ⎜ 2 ⎟ + t ⋅ ⎜ −2 ⎟ ; t ∈ \
⎜3⎟
⎜ 5⎟
⎝ ⎠
⎝ ⎠
⎛ 3⎞
⎛ 2⎞
G ⎜ ⎟
⎜ ⎟
c) Z. B.: g: x = ⎜ −2 ⎟ + t ⋅ ⎜ −2 ⎟ ; t ∈ \
⎜ 5⎟
⎜ 5⎟
⎝ ⎠
⎝ ⎠
⎛ 3⎞
⎛ 3⎞
G ⎜ ⎟
⎜ ⎟
oder g: x = ⎜ −2 ⎟ + t ⋅ ⎜ −2 ⎟ ; t ∈ \
⎜ 5⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
JJJG JJJJG
JJJJG
JJJJG
8. Ebene P1P2 P3 : OX = OP1 + λ P1P2 + μ P1P3
JJJG JJJG
JJJG
Gerade AB: OX = OA + ϕ ⋅ AB
JJJJG
JJJJG
JJJG JJJG JJJJG
λ P1P2 + μ P1P3 − ϕAB = OA − OP1
Für einen Schnittpunkt müssen wir Parameter λ, μ und ϕ finden.
⎛ −7 ⎞
⎛ 14 ⎞
⎛ −3 ⎞ ⎛ 2 ⎞
λ ⎜ 5 ⎟ + μ ⎜ −10 ⎟ − ϕ ⎜ 3 ⎟ = ⎜ −2 ⎟
⎜⎜ ⎟⎟
⎜⎜
⎟⎟
⎜⎜ ⎟⎟ ⎜⎜
⎟⎟
⎝ −3 ⎠
⎝ −2 ⎠
⎝ 15 ⎠ ⎝ −14 ⎠
λ = 1, ϕ = 23 und μ = 21 .
S(−1 | 3 | 1)
224
274
9. Ebene, in der das Parallelogramm liegt:
⎛1⎞
⎛2⎞
⎛0⎞
G ⎜ ⎟
⎜
⎟
E: x = 2 + r 3 + s ⎜ 2 ⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝0⎠
⎝0⎠
⎝6⎠
Schnittpunkt von g mit E:
( − 319 | − 3659 | 109
12 )
> 1 und r = − 20
< 0.
9
Alle Punkte des Parallelogramms werden beschrieben für Parameterwerte
0 ≤ s ≤ 1 und 0 ≤ r ≤ 1.
Die Gerade trifft nicht das Parallelogramm.
für Parameterwerte s =
275
109
72
⎛0⎞
⎛0⎞ ⎛1⎞
G ⎜ ⎟
⎜ ⎟ ⎜ ⎟
10. a) Z. B.: E: x = ⎜ 2 ⎟ + r ⋅ ⎜ 0 ⎟ + s ⎜ 0 ⎟
⎜0⎟
⎜1⎟ ⎜0⎟
⎝ ⎠
⎝ ⎠ ⎝ ⎠
1
⎛ ⎞
⎛0⎞ ⎛0⎞
G ⎜ ⎟
⎜ ⎟ ⎜ ⎟
b) Z. B.: E: x = ⎜ 0 ⎟ + r ⋅ ⎜ 1 ⎟ + s ⎜ 0 ⎟
⎜0⎟
⎜0⎟ ⎜1⎟
⎝ ⎠
⎝ ⎠ ⎝ ⎠
11. Das Tauchboot taucht auf im Punkt (13 | 0 | 0).
12. Für a = −1 sind die 3 Richtungsvektoren linear abhängig und somit Ebene
und Gerade parallel. Der Stützvektor der Geraden liegt nicht in der Ebene.
13. Beispiel:
⎛ 3⎞
⎛ −1 ⎞ ⎛ 1 ⎞
G ⎜ ⎟
E1 : x = 1 + s ⎜ 1 ⎟ + t ⎜ 0 ⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝ −2 ⎠
⎝ 2 ⎠ ⎝0⎠
⎛1⎞
⎛ 1 ⎞ ⎛ −1 ⎞
G
E2 : x = ⎜1⎟ + s⎜ 0 ⎟ + t ⎜ 1 ⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝3⎠
⎝0⎠ ⎝ 2 ⎠
⎛1⎞
⎛ −1 ⎞ ⎛ 2 ⎞
G
E3 : x = ⎜ 1 ⎟ + s ⎜ 1 ⎟ + t ⎜ 0 ⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝3⎠
⎝ 2 ⎠ ⎝ −5 ⎠
225
275
⎛0⎞
⎛ 0⎞
⎛ −9 ⎞
⎛ −3 ⎞
⎛ −3 ⎞
⎛ 0⎞
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
E 2 : 11 + λ ⋅ 0 + μ ⋅ ⎜ −3 ⎟
14. E1 : 4 + λ ⋅ 4 + μ ⋅ 0
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ 7⎠
⎝ −3 ⎠
⎝ 0⎠
⎝ 4⎠
⎝ 2⎠
⎝ 0⎠
⎛0⎞
⎛2⎞
G
G
⎜
⎟
E1 : 3 * x = 40
E2 : ⎜ 0 ⎟ * x = 6
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝4⎠
⎝3⎠
Ermitteln Durchstoßpunkt S:
E1 : 3x 2 + 4x3 = 40
Einsetzen von x1 = −2; x 2 = 6 ⇒ x3 = 5,5
S = (−2 | 6 | 5,5)
15. a) B(4 | 4 | 0); C(−4 | 4 | 0); D(−4 | −4 | 0); E(0 | 0 | 16); P(2 | −2 | 8)
b) S(−0,857 | −0,857 | 12,571)
c) Man benötigt lediglich Richtungsvektoren
JJJG ⎛ −4 ⎞ JJJG ⎛ 4 ⎞
BE = ⎜ −4 ⎟ ; QR = ⎜ 2 ⎟
⎜ 16 ⎟
⎜ −8 ⎟
⎝ ⎠
⎝ ⎠
JJJG JJJG
BE ∗ QR
JJJG
BE ⋅ QR
cos ϕ = JJJG
= −152 ⇒ ϕ = 12, 24°
24 42
4.4.3 Lagebeziehungen zwischen Ebenen
277
2. a) Gleichsetzen führt auf das Gleichungssystem
5r − s − 4k − 2t = 4
r−k−t =1
6s − 6k − 18t = 6 ⇒ s − k − 3t = 1
2r + 3s − 5k − 11t = 5
0=0
Das Gleichungssystem hat 2 freie Parameter, d. h. die Schnittmenge
sind die Ebenen selber; sie sind identisch.
Alternativ:
Richtungsvektoren vergleichen:
⎛ 4 ⎞ ⎛ 5 ⎞ ⎛ −1⎞
⎛ 2 ⎞ ⎛ 5⎞
⎛ −1⎞
⎜ 6 ⎟ = ⎜ 0 ⎟ + ⎜ 6 ⎟ ; ⎜ 18 ⎟ = ⎜ 0 ⎟ + 3 ⎜ 6 ⎟
⎜ 5⎟ ⎜ 2⎟ ⎜ 3 ⎟
⎜ 11 ⎟ ⎜ 2 ⎟
⎜3⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎝ ⎠ ⎝ ⎠
⎝ ⎠
und Stützvektor von E liegt in F für r = −1; s = 0.
226
277
2. b) Beispiele:
0
⎛5⎞
⎛2⎞
G ⎛ ⎞
E: x = ⎜ 8 ⎟ + r ⎜ 0 ⎟ + s ⎜ 18 ⎟ mit r, s ∈ \
⎜ 4⎟
⎜ 2⎟
⎜ 11 ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
1
⎛ 4⎞
⎛ −1 ⎞
G ⎛ ⎞
E: x = ⎜ 2 ⎟ + r ⎜ 6 ⎟ + s ⎜ 6 ⎟ mit r, s ∈ \
⎜1⎟
⎜5⎟
⎜3⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
−4
⎛6⎞
⎛0⎞
G ⎛ ⎞
E: x = ⎜ 2 ⎟ + r ⎜ 24 ⎟ + s ⎜ 30 ⎟ mit r, s ∈ \
⎜ −1 ⎟
⎜ 16 ⎟
⎜ 17 ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
3. Die Punkte der Schnittgeraden liegen sowohl in der Ebene E1 , als auch
in der Ebene E 2 , die z. B. durch die Punkte B, E und A gegeben ist.
⎛0⎞ ⎛ 6 ⎞
JJJG
JJJG ⎛ 0 ⎞
G JJJG
E 2 : x = OB + k ⋅ BE + t ⋅ BA = ⎜ 8 ⎟ + k ⎜ 0 ⎟ + t ⎜ −8 ⎟ ; k, t ∈ \
⎜0⎟
⎜ 4⎟ ⎜ 0 ⎟
⎝ ⎠
⎝ ⎠ ⎝ ⎠
Gleichsetzen von E1 und E 2 liefert:
−3r − 3s − 6t = −6
r=0
4s + 8t = 8 ⇒ s + 2t = 2
−4r − 4s − 4k = −4
k − 2t = −1
Einsetzen von k = −1 + 2t gibt die gesuchte Gerade
0
6
G ⎛ ⎞ ⎛ ⎞
g: x = ⎜ 8 ⎟ + t ⎜ −8 ⎟ ; t ∈ \
⎜ −4 ⎟ ⎜ 0 ⎟
⎝ ⎠ ⎝ ⎠
4. E : −3x1 + 6x 2 + 4x3 = 36
a) F : 3x1 + 6x 2 + 4x3 = 18
b) F : 3x1 + 6x 2 + 4x3 = 36
c) F : 3x1 − 3x 2 + 4x3 = 0
d) F : x1 − x 2 + x3 = −2
⎛ 0 ⎞
⎛ −3 ⎞
⎜ 2⎟
G ⎜
⎟
Schnitt mit: x = 4, 5 + t ⋅ ⎜ − 3 ⎟
⎜⎜
⎟⎟
⎜ 1 ⎟
⎝ 0 ⎠
⎝ ⎠
⎛ 0 ⎞
⎛0⎞
⎜ ⎟
G ⎜ ⎟
Schnitt mit: x = 6 + t ⋅ ⎜ − 23 ⎟
⎜⎜ ⎟⎟
⎜ 1 ⎟
⎝0⎠
⎝ ⎠
⎛ −4 ⎞
⎛ 12 ⎞
⎜ ⎟
G ⎜ ⎟
Schnitt mit: x = 12 + t ⋅ ⎜ − 83 ⎟
⎜⎜ ⎟⎟
⎜ 1 ⎟
⎝0⎠
⎝ ⎠
⎛ 18 ⎞
⎛ −20 ⎞
G ⎜ ⎟
Schnitt mit: x = 17 + t ⋅ ⎜ −14 ⎟
⎜⎜ ⎟⎟
⎜⎜
⎟⎟
⎝ −3 ⎠
⎝ 6 ⎠
227
278
4
⎛0⎞
G ⎛ ⎞
5. a) Die Ebenen schneiden sich in g: x = ⎜ 2 ⎟ + s ⎜ 1 ⎟ ; s ∈ \ .
⎜5⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
b) Die Ebenen sind identisch.
−9, 6 ⎞
⎛ −5 ⎞
G ⎛
c) Die Ebenen schneiden sich in g: x = ⎜ −2, 4 ⎟ + s ⎜ −2 ⎟ ; s ∈ \ .
⎜ 0 ⎟
⎜ −1 ⎟
⎝
⎠
⎝ ⎠
0,5 ⎞
⎛ 2⎞
G ⎛
d) Die Ebenen schneiden sich in g: x = ⎜ 1,5 ⎟ + s ⎜ 1 ⎟ ; s ∈ \ .
⎜ 1,5 ⎟
⎜ 0⎟
⎝
⎠
⎝ ⎠
2
⎛ 9⎞
G ⎛ ⎞
e) Die Ebenen schneiden sich in g: x = ⎜ 6 ⎟ + s ⎜ −7 ⎟ ; s ∈ \ .
⎜9⎟
⎜ 10 ⎟
⎝ ⎠
⎝ ⎠
⎛3⎞ ⎛ 1 ⎞
⎛ 2⎞
G ⎜ ⎟ ⎜ ⎟
6. Z. B.: E1 : x = 2 + t −2 + s ⎜ −2 ⎟ ; s, t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ −1 ⎠ ⎝ 2 ⎠
⎝ 2⎠
⎛3⎞ ⎛ 1 ⎞
⎛ −6 ⎞
G ⎜ ⎟ ⎜ ⎟
Z. B.: E 2 : x = 2 + t −2 + r ⎜ 0 ⎟ ; t, r ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ −1 ⎠ ⎝ 2 ⎠
⎝ −3 ⎠
7. Beispiele:
⎛0⎞
⎛0⎞ ⎛1⎞
G
E1 : x = ⎜ 0 ⎟ + s ⎜ 0 ⎟ + t ⎜ 0 ⎟ ; s, t ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝1⎠
⎝2⎠ ⎝0⎠
⎛0⎞
⎛0⎞ ⎛0⎞
G
E 2 : x = ⎜ 0 ⎟ + s ⎜ 0 ⎟ + t ⎜ 1 ⎟ ; s, t ∈ \ oder
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝2⎠
⎝1⎠ ⎝0⎠
⎛0⎞
⎛0⎞ ⎛1⎞
G
E1 : x = ⎜ 0 ⎟ + s ⎜ 0 ⎟ + t ⎜ 1 ⎟ ; s, t ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝ 5⎠
⎝1⎠ ⎝0⎠
⎛ 2⎞
⎛ 0 ⎞ ⎛ −1 ⎞
G
E 2 : x = ⎜ −2 ⎟ + s ⎜ 0 ⎟ + t ⎜ 1 ⎟ ; s, t ∈ \
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎝0 ⎠
⎝3⎠ ⎝ 0 ⎠
228
278
⎛ 1 ⎞ ⎛ 5⎞
⎛ −3 ⎞
G ⎜ ⎟ ⎜ ⎟
8. a) Z. B.: E 2 : x = 0 + t 4 + s ⎜ 3 ⎟ ; s, t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝ −4 ⎠ ⎝ 3 ⎠
⎝ −4 ⎠
⎛1⎞ ⎛ 1 ⎞
⎛0⎞
G ⎜ ⎟ ⎜ ⎟
b) Z. B.: E: x = 1 + t 0 + s ⎜ 0 ⎟ ; s, t ∈ \
⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
⎝1⎠ ⎝ 0 ⎠
⎝1⎠
c) 9. a) Die Ebenen E1 und E 2 sind parallel.
2
⎛ −1 ⎞
⎛ 2⎞
G ⎛ ⎞
b) E 3 : x = ⎜ 1 ⎟ + r ⋅ ⎜ 4 ⎟ + t ⋅ ⎜ 1 ⎟ ; r, t ∈ \
⎜6⎟
⎜0⎟
⎜ 3⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
0
⎛ −1⎞
⎛ 2⎞
G ⎛ ⎞
c) z. B.: E: x = ⎜ 0 ⎟ + r ⋅ ⎜ 4 ⎟ + t ⋅ ⎜ 1 ⎟
⎜0⎟
⎜0⎟
⎜ 3⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
1⎞
−2 ⎞
⎛
⎛
⎛ 2⎞
G
E: x = ⎜ 0 ⎟ + r ⋅ ⎜ 8 ⎟ + t ⋅ ⎜ 1 ⎟
⎜0⎟
⎜ 0⎟
⎜ 3⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
6
⎛ −2 ⎞
⎛1⎞
G ⎛ ⎞
E: x = ⎜ 3 ⎟ + r ⋅ ⎜ 8 ⎟ + t ⋅ ⎜ 5 ⎟
⎜6⎟
⎜ 0⎟
⎜ 3⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎛1⎞
10. E ist parallel zur x1x 2 -Ebene, wie man an den Richtungsvektoren ⎜ −3 ⎟
⎜0⎟
⎝ ⎠
⎛ −2 ⎞
und ⎜ 1 ⎟ direkt sieht.
⎜ 0⎟
⎝ ⎠
4
⎛0⎞
⎛ −2 ⎞
G ⎛ ⎞
11. Z. B: E: x = ⎜ 1 ⎟ + r ⋅ ⎜ 3 ⎟ + t ⋅ ⎜ 3 ⎟
⎜ 4⎟
⎜ −3 ⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
E1 schneidet E in einer Geraden.
E 2 ist zu E echt parallel.
E 3 schneidet E in einer Geraden.
229
278
12. Beispiele
1
⎛1⎞
⎛1⎞
G ⎛ ⎞
(1) • E1: x = ⎜ 0 ⎟ + r ⎜ 0 ⎟ + s ⎜ 1 ⎟
⎜0⎟
⎜0⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
2
2
⎛ ⎞
⎛0⎞
G ⎛ ⎞
• E1 : x = ⎜ 1 ⎟ + r ⎜ 1 ⎟ + s ⎜ 1 ⎟
⎜0⎟
⎜0⎟
⎜0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
2
⎛1⎞
⎛ 0⎞
G ⎛ ⎞
E2: x = ⎜ 0 ⎟ + r ⎜ 0⎟ + s ⎜ 1 ⎟
⎜0⎟
⎜0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
0
1
⎛ ⎞
⎛ 0⎞
G ⎛ ⎞
E2: x = ⎜ 0⎟ + r ⎜ 0⎟ + s ⎜ 0⎟
⎜0⎟
⎜ 0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
0
⎛0⎞
⎛1⎞
G ⎛ ⎞
(2) • E1: x = ⎜ 1 ⎟ + r ⎜ 1 ⎟ + s ⎜ 0 ⎟
⎜0⎟
⎜0⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
8
⎛ 2⎞
⎛ −2 ⎞
G ⎛ ⎞
• E1 : x = ⎜ 1 ⎟ + r ⎜ 1 ⎟ + s ⎜ 0 ⎟
⎜0⎟
⎜ 0⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
−3
⎛ 3⎞
⎛ 4⎞
G ⎛ ⎞
E2: x = ⎜ 0 ⎟ + r ⎜ 4⎟ + s ⎜ 4⎟
⎜0⎟
⎜ 3⎟
⎜ 3⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
0
⎛ 0⎞
⎛ 0⎞
G ⎛ ⎞
E2: x = ⎜ 1 ⎟ + r ⎜ 1⎟ + s ⎜ 0⎟
⎜0⎟
⎜ 0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
0
⎛0⎞
⎛ 0⎞
G ⎛ ⎞
E2: x = ⎜ 3⎟ + r ⎜ 1 ⎟ + s ⎜ 0 ⎟
⎜0⎟
⎜ 3⎟
⎜ −6 ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
0
⎛1⎞
⎛ −1 ⎞
G ⎛ ⎞
• E1 : x = ⎜ 2 ⎟ + r ⎜ 2 ⎟ + s ⎜ 0 ⎟
⎜0⎟
⎜ 3⎟
⎜ −3 ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
0
⎛0⎞
⎛1⎞
G ⎛ ⎞
(3) • E1: x = ⎜ 0 ⎟ + r ⎜ 0 ⎟ + s ⎜ 0 ⎟
⎜1⎟
⎜1⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
0
⎛ 2⎞
⎛ −2 ⎞
G ⎛ ⎞
• E1 : x = ⎜ 0 ⎟ + r ⎜ 7 ⎟ + s ⎜ −7 ⎟
⎜ 3⎟
⎜ 4⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
0
⎛6⎞
⎛ 12 ⎞
G ⎛ ⎞
• E1: x = ⎜ 0 ⎟ + r ⎜ 7 ⎟ + s ⎜ 14 ⎟
⎜ 2⎟
⎜8⎟
⎜ 14 ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
3
⎛ 3⎞
⎛ −6 ⎞
G ⎛ ⎞
E2: x = ⎜ 2⎟ + r ⎜1⎟ + s ⎜ 4 ⎟
⎜5⎟
⎜ 5⎟
⎜ −10 ⎟
⎝ ⎠
⎝ ⎠
⎝
⎠
0
⎛ 0⎞
⎛ 0⎞
G ⎛ ⎞
E2: x = ⎜ 0⎟ + r ⎜ 0⎟ + s ⎜ 1 ⎟
⎜1⎟
⎜1⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
6
⎛ 3⎞
⎛ 1⎞
G ⎛ ⎞
E 2 : x = ⎜ 6 ⎟ + r ⎜ 3 ⎟ + s ⎜ 1⎟
⎜7⎟
⎜ 4⎟
⎜ 1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
1
⎛ 1⎞
⎛ 0⎞
G ⎛ ⎞
E 2 : x = ⎜ 1 ⎟ + r ⎜ 1⎟ + s ⎜ 0 ⎟
⎜ 2⎟
⎜ 1⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
0
⎛ 1⎞
⎛1⎞
G ⎛ ⎞
(4) • E1: x = ⎜ 0 ⎟ + r ⎜ 1⎟ + s ⎜ 0 ⎟
⎜0⎟
⎜ 1⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
1
⎛1⎞
⎛ 0⎞
G ⎛ ⎞
• E1 : x = ⎜ 3 ⎟ + r ⎜ 2 ⎟ + s ⎜ 1 ⎟
⎜5⎟
⎜ 3⎟
⎜ 2⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
1
⎛ 6⎞
⎛7⎞
G ⎛ ⎞
• E1 : x = ⎜ 1 ⎟ + r ⎜ 1 ⎟ + s ⎜ 2 ⎟
⎜ 1⎟
⎜ 4⎟
⎜ 5⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
0
⎛ 1⎞
⎛ 0⎞
G ⎛ ⎞
E 2 : x = ⎜ 1 ⎟ + r ⎜ 1⎟ + s ⎜ 1 ⎟
⎜0⎟
⎜ 1⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
5
⎛ 3⎞
⎛1⎞
G ⎛ ⎞
E 2: x = ⎜ 4 ⎟ + r ⎜ 3⎟ + s ⎜ 0 ⎟
⎜ 4⎟
⎜ 3⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
5
⎛ 3⎞
⎛ −2 ⎞
G ⎛ ⎞
E 2 : x = ⎜ 9 ⎟ + r ⎜ 5 ⎟ + s ⎜ −4 ⎟
⎜ −1⎟
⎜0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
2
⎛5⎞
⎛ 2⎞
G ⎛ ⎞
• E1 : x = ⎜ 1 ⎟ + r ⎜ 0 ⎟ + s ⎜ 2 ⎟
⎜1⎟
⎜0⎟
⎜ 2⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
230
4.5 Normalenvektor einer Ebene
4.5.1 Normalenvektor und Koordinatengleichung einer Ebene
283
3
G
G ⎛ ⎞
2. a) n ablesen: n = ⎜ −2 ⎟
⎜ 6⎟
⎝ ⎠
Punkt P bestimmen x 2 = x 3 = 0 : P(6 | 0 | 0)
⎛ 3 ⎞ ⎡⎛ x 1 ⎞ ⎛ 6 ⎞ ⎤
⇒ Normalenform: E: ⎜ −2 ⎟ ∗ ⎢⎜ x 2 ⎟ − ⎜ 0 ⎟ ⎥ = 0
⎜ 6 ⎟ ⎢⎜ x ⎟ ⎜ 0 ⎟ ⎥
⎝ ⎠ ⎣⎝ 3 ⎠ ⎝ ⎠ ⎦
a
G ⎛ ⎞
b) Normalenvektor ablesbar: n = ⎜ b ⎟ bzw. Vielfache davon
⎜c⎟
⎝ ⎠
a
⎛ ⎞
G
n = r ⋅ ⎜ b ⎟ ; r ∈ \ \ {0}
⎜c⎟
⎝ ⎠
284
3. a) Die 3 Punkte dürfen nicht auf einer Geraden liegen.
Beispiel: P(0 | 3 | 0); Q(12 | 0 | 0); R(0 | 0 | 2) liefert
0
⎛ 12 ⎞
⎛0⎞
G ⎛ ⎞
E: x = ⎜ 3 ⎟ + r ⎜ −3 ⎟ + s ⎜ −3 ⎟
⎜0⎟
⎜0⎟
⎜ 2⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
b) (1) x1 = 6 − 4x 2 − 6x 3
(2) x 2 = s; x 3 = t
x1 = 6 − 4s − 6t
x2 = s
x3 = t
6
⎛ −4 ⎞ ⎛ −6 ⎞
G ⎛ ⎞
(3) x = ⎜ 0 ⎟ + s ⎜ 1 ⎟ + t ⎜ 0 ⎟
⎜0⎟
⎜ 0⎟ ⎜ 1⎟
⎝ ⎠
⎝ ⎠ ⎝ ⎠
231
284
4. a)
E1 ist parallel zur
x1 - und x 3 -Achse .
E 2 ist parallel zur
x 3 -Achse .
b) d = 0; a, b, c beliebig: Ebene beinhaltet Ursprung
a = 0; b ≠ 0; c ≠ 0: Ebene parallel zur x1 -Achse
a = 0; b = 0; c ≠ 0: Ebene parallel zur x1x 2 -Ebene
a = 0; b ≠ 0; c = 0: Ebene parallel zur x1x 3 -Ebene
a ≠ 0; b = 0; c ≠ 0: Ebene parallel zur x 2 -Achse
a ≠ 0; b = 0; c = 0: Ebene parallel zur x 2 x 3 -Ebene
a ≠ 0; b ≠ 0; c = 0: Ebene parallel zur x 3 -Achse
232
284
5. Überprüfe, ob die Normalenvektoren Vielfache voneinander sind, also ob
JJG
JJG
n1 = s ⋅ n 2 mit s ∈ \.
Ja:
Überprüfe, ob Normalengleichungen äquivalent sind, d. h. multipliziere die Normalengleichung von E 2 mit s und überprüfe, ob dies
die von E1 ist.
Nein: Die Ebenen schneiden sich in einer Geraden g.
285
6. a) Ebene des Sockels
⎛ 2 ⎞ ⎡⎛ x1 ⎞ ⎛ 17 ⎞ ⎤
E: ⎜ 5 ⎟ ∗ ⎢⎜ x 2 ⎟ − ⎜ −8 ⎟ ⎥ = 0
⎜ −8 ⎟ ⎢⎜ x ⎟ ⎜ 19 ⎟ ⎥
⎝ ⎠ ⎣⎝ 3 ⎠ ⎝ ⎠ ⎦
Prüfe B ∈ E:
⎛ 2 ⎞ ⎡⎛ 29 ⎞ ⎛ 17 ⎞ ⎤ ⎛ 2 ⎞ ⎛ 12 ⎞
⎜ 5 ⎟ ∗ ⎢⎜ −24 ⎟ − ⎜ −8 ⎟ ⎥ = ⎜ 5 ⎟ ∗ ⎜ −16 ⎟ = 0 ⇒ B ∈ E
⎜ −8 ⎟ ⎢⎜ 12 ⎟ ⎜ 19 ⎟ ⎥ ⎜ −8 ⎟ ⎜ −7 ⎟
⎝ ⎠ ⎣⎝
⎠ ⎝ ⎠⎦ ⎝ ⎠ ⎝
⎠
Prüfe C ∈ E:
⎛ 2 ⎞ ⎡⎛ 11 ⎞ ⎛ 17 ⎞ ⎤ ⎛ 2 ⎞ ⎛ −6 ⎞
⎜ 5 ⎟ ∗ ⎢⎜ 5 ⎟ − ⎜ −8 ⎟ ⎥ = ⎜ 5 ⎟ ∗ ⎜ 13 ⎟ = 45 ≠ 0 ⇒ C ∉ E.
⎜ −8 ⎟ ⎢⎜ 20 ⎟ ⎜ 19 ⎟ ⎥ ⎜ −8 ⎟ ⎜ 1 ⎟
⎝ ⎠ ⎣⎝ ⎠ ⎝ ⎠ ⎦ ⎝ ⎠ ⎝ ⎠
b) x liegt genau dann in E, wenn die Gleichung
⎛ 2 ⎞ ⎡⎛ x1 ⎞ ⎛ 17 ⎞ ⎤
⎜ 5 ⎟ ∗ ⎢⎜ x 2 ⎟ − ⎜ −8 ⎟ ⎥ = 0 gilt.
⎜ −8 ⎟ ⎢⎜ ⎟ ⎜ 19 ⎟ ⎥
⎝ ⎠ ⎣⎝ x 3 ⎠ ⎝ ⎠ ⎦
⎛ 2 ⎞ ⎡⎛ x1 ⎞ ⎛ 2 ⎞ ⎤
7. a) E: ⎜ 1 ⎟ ∗ ⎢⎜ x 2 ⎟ − ⎜ 3 ⎟ ⎥ = 0 ⇔ 2x1 + x 2 + 2x 3 = 11
⎜ 2 ⎟ ⎢⎜ ⎟ ⎜ 2 ⎟ ⎥
⎝ ⎠ ⎣⎝ x 3 ⎠ ⎝ ⎠ ⎦
⎛ 4 ⎞ ⎡⎛ x1 ⎞ ⎛ 6 ⎞ ⎤
b) E: ⎜ 0 ⎟ ∗ ⎢⎜ x 2 ⎟ − ⎜ −2 ⎟ ⎥ = 0 ⇔ 4x1 − 3x 2 = 15
⎜ −3 ⎟ ⎢⎜ x ⎟ ⎜ 3 ⎟ ⎥
⎝ ⎠ ⎣⎝ 3 ⎠ ⎝ ⎠ ⎦
⎛ 0 ⎞ ⎡⎛ x 1 ⎞ ⎛ 2 ⎞ ⎤
c) E: ⎜ 0 ⎟ ∗ ⎢⎜ x 2 ⎟ − ⎜ −3 ⎟ ⎥ = 0 ⇔ x 3 = 5
⎜ 1 ⎟ ⎢⎜ x ⎟ ⎜ 5 ⎟ ⎥
⎝ ⎠ ⎣⎝ 3 ⎠ ⎝ ⎠ ⎦
8. a) P ∉ E; Q ∉ E; R ∈ E
b) P ∉ E; Q ∈ E; R ∉ E
9. a) E:
b) E:
x2
3
x1
3
+
x3
4
c) P ∈ E; Q ∈ E; R ∈ E
d) P ∈ E; Q ∈ E; R ∈ E
= 1 ⇔ E: 4x 2 + 3x 2 = 12
= 1 ⇔ x1 = 3
233
285
x
9. c) E: x1 + 2 = 1 ⇔ 3x1 + x 2 = 3
3
d) E:
286
x1
2
+
x3
4
= 1 ⇔ 2x1 + x 3 = 4
10. a) (5) S1 (0 | 0 | 0); S 2 (0 | 0 | 0); S3 (0 | 0 | 0)
(6) S1 (4 | 0 | 0); S 2 (0 | 2 | 0); S3 existiert nicht
b) Setze 2 Koordinaten null und löse die entstehende Gleichung für die
3. Koordinate.
234
286
11. a) E:
b) E:
c) E:
x
x2
+ 3 = 1 ⇔ E: 6x1 + 4x 2 + 3x 3 = 12
3
4
x3
x2
x1 +
−
= 1 ⇔ E: 12x1 + 4x 2 − 3x 3 = 12
3
4
x
x
x
− 1 + 2 + 3 = 1 ⇔ E: − 5x1 + 2x 2 + 5x 3 = 10
2
5
2
x1
2
+
12. a) parallel zur x 3 -Achse
3
⎛ −3 ⎞
⎛ 0⎞
G ⎛ ⎞
z. B. E: x = ⎜ 0 ⎟ + r ⎜ 2 ⎟ + s ⎜ 0 ⎟ ; r, s ∈ \
⎜0⎟
⎜0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
b) parallel zur x1 -Achse
0
⎛ 0⎞
⎛1⎞
G ⎛ ⎞
z. B. E: x = ⎜ 4 ⎟ + r ⎜ −2 ⎟ + s ⎜ 0 ⎟ ; r, s ∈ \
⎜0⎟
⎜1⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
235
286
12. c) E beinhaltet die x 3 -Achse
⎛1⎞
⎛0⎞
G
z. B. E: x = r ⎜ 1 ⎟ + s ⎜ 0 ⎟ ; r, s ∈ \
⎜0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
d) parallel zur x 2 -x 3 -Ebene
2
⎛0⎞
⎛ 0⎞
G ⎛ ⎞
z. B. E: x = ⎜ 0 ⎟ + r ⎜ 1 ⎟ + s ⎜ 0 ⎟ ; r, s ∈ \
⎜0⎟
⎜0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
236
286
12. e) E ist die x1 -x 3 -Ebene
⎛1⎞
⎛0⎞
G
z. B. E: x = r ⎜ 0 ⎟ + s ⎜ 0 ⎟ ; r, s ∈ \
⎜0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
f) parallel zur x1 -x 2 -Ebene
0
⎛1⎞
⎛0⎞
G ⎛ ⎞
z. B. E: x = ⎜ 0 ⎟ + r ⎜ 0 ⎟ + s ⎜ 1 ⎟ ; r, s ∈ \
⎜ −2 ⎟
⎜0⎟
⎜0⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
x1 -x 2 -Ebene: x 3 = 0
x1 -x 3 -Ebene: x 2 = 0
x 2 -x 3 -Ebene: x1 = 0
Genau 2 Vorfaktoren von den Variablen müssen null ergeben.
13. Koordinatenebenen:
t 2 − 1 = 0 ⇒ t = 1 oder t = 1
−2t −2 = 0 ⇒ t = −1
t 2 + t = 0 ⇒ t = 0 oder t = −1
Es gibt keinen Parameterwert für t, sodass 2 Vorfaktoren gleichzeitig
verschwinden. E t ist nie parallel zu einer Koordinatenebene.
237
286
2
⎛ −1⎞ ⎛ 1 ⎞
G ⎛ ⎞
14. a) E: x = ⎜ 0 ⎟ + s ⎜ 1 ⎟ + t ⎜ 0 ⎟
⎜0⎟
⎜ 0 ⎟ ⎜1⎟
⎝ ⎠
⎝ ⎠ ⎝ ⎠
5
⎛ −3 ⎞ ⎛ 1 ⎞
G ⎛ ⎞
c) E: x = ⎜ 0 ⎟ + s ⎜ 1 ⎟ + t ⎜ 0 ⎟
⎜0⎟
⎜ 0 ⎟ ⎜1⎟
⎝ ⎠
⎝ ⎠ ⎝ ⎠
⎛2⎞ ⎛1⎞
1⎞
⎛
⎜ 3⎟ ⎜3⎟
G
d) E: x = ⎜ 0 ⎟ + s ⎜ 1 ⎟ + t ⎜ 0 ⎟
⎜0⎟
⎜ ⎟ ⎜ ⎟
⎝ ⎠
⎝ 0⎠ ⎝1⎠
⎛− 1 ⎞
⎛ 1 ⎞ ⎛− 1 ⎞
⎜2⎟ ⎜ 2⎟
G ⎜ 2⎟
b) E: x = ⎜ 0 ⎟ + s ⎜ 1 ⎟ + t ⎜ 0 ⎟
⎜ 0 ⎟
⎜0⎟ ⎜ 1 ⎟
⎝ ⎠
⎝ ⎠ ⎝ ⎠
15. a) E1: 2x1 − 3x 2 + x 3 = 0
b) E1: 4x1 − 2x 2 + x 3 = 0
E 2 : 2x1 − 3x 2 + x 3 = 1
E 2 : 4x1 − 2x 2 + x 3 = 1
c) E1: x1 − x 3 = 1
d) E1: x 2 + 2x 3 = 0
E 2 : x1 − x 3 = 2
E 2 : x 2 + 2x 3 = 1
16. Koordinatengleichung: E: x1 = p1
17. a) 6t + 12t + 16 − 6t = 0 ⇔ t = − 4
3
JJG ⎛ 3t ⎞
b) Normalenvektor von E t : n t = ⎜ 4t ⎟ muss ein Vielfaches des
⎜3⎟
⎝ ⎠
⎛ 3t ⎞
⎛ 3⎞
Richtungsvektors der Geraden sein: ⎜ 4t ⎟ = r ⋅ ⎜ 4 ⎟ ⇒ t = 3; r = 3
⎜3⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
E: 9x1 + 12x 2 + 3x 3 − 18 = 0
238
4.5.2 Abstandsberechnungen
287
5
3
G ⎛ ⎞
G ⎛ ⎞
2. a) Normalenvektor von E: n = ⎜ −1⎟ ; Richtungsvektor von g: u = ⎜ 7 ⎟
⎜ −4 ⎟
⎜2⎟
⎝ ⎠
⎝ ⎠
G
G G
n ⋅ u = 0 ⇒ die Gerade steht senkrecht auf n .
Wegen (11 | -11 | 1) ∉ E ist g & E .
b)
Man wählt einen beliebigen Punkt P der Geraden und berechnet
den Abstand des Punktes zur Ebene:
11 ⎞ ⎛ 3 ⎞
3
G ⎛ ⎞
G ⎛
Z. B.: P(11 | −11 | 1); n = ⎜ −1⎟ ⇒ h: x = ⎜ −11⎟ + t ⎜ −1⎟
⎜2⎟
⎜ 1 ⎟ ⎜2⎟
⎝ ⎠
⎝
⎠ ⎝ ⎠
Schnittpunkt von h mit E: F(5 | −9 | −3)
⎛ 6⎞
JJG
PF = ⎜ −2 ⎟ = 2 14 ≈ 7, 48
⎜ 4⎟
⎝ ⎠
288
3. a) Die Normalenvektoren sind Vielfache voneinander
JJG ⎛ 10 ⎞ JJG ⎛ −20 ⎞
n1 = ⎜ −2 ⎟ ; n 2 = ⎜ 4 ⎟
⎜ 11 ⎟
⎜ −22 ⎟
⎝
⎠
⎝ ⎠
Jedoch ist z. B. (3 | 0 | 0) ein Punkt von E1 aber nicht von E 2 .
Die Ebenen sind parallel aber verschieden.
239
288
3. b)
Man wählt beliebig einen Punkt P auf Ebene E1 und berechnet
den Abstand des Punktes P zur Ebene E 2 :
3
10
10
G ⎛ ⎞
G ⎛ ⎞ ⎛ ⎞
Z. B.: P(3 | 0 | 0); n = ⎜ −2 ⎟ ⇒ g: x = ⎜ 0 ⎟ + t ⎜ −2 ⎟
⎜ 11 ⎟
⎜ 0 ⎟ ⎜ 11 ⎟
⎝ ⎠
⎝ ⎠ ⎝ ⎠
(
Schnittpunkt von g mit E 2 : F 1
2
5
−
⎛ 3 ⎞ ⎡ G ⎛ 4 ⎞⎤
4. Hilfsebene: E: ⎜ −2 ⎟ ∗ ⎢ x − ⎜ −5 ⎟ ⎥ = 0
⎜ 4⎟ ⎢
⎜ 8 ⎟⎥
⎝ ⎠ ⎣
⎝ ⎠⎦
Schnittpunkt von E und g: F
JJG
FP = 6 ⋅
(
216
29
1
29
230
29
11
5
)
⎛ 2 ⎞
JJG
; PF = ⎜⎜ − 2 ⎟⎟ = 3
5
⎜ 11 ⎟
⎝ 5 ⎠
) für s =
14
29
30
29
5. Abst(g; h) = 2949
29
Für parallele Geraden wählt man einen beliebigen Punkt P der ersten
Geraden und berechnet den Abstand zwischen P und der zweiten Geraden.
289
6. a) Siehe Information auf S. 288
−6
2
G ⎛ ⎞ ⎛ ⎞
b) Lotgerade durch P: g: x = ⎜ 5 ⎟ + t ⎜ −2 ⎟
⎜ 5⎟ ⎜1⎟
⎝ ⎠ ⎝ ⎠
Schnittpunkt mit der Ebene: F(−2 | 1 | 7)
JJG ⎛ −4 ⎞ JJG
Differenzvektor FP = ⎜ 4 ⎟ ; FP = 36 = 6
⎜ −2 ⎟
⎝ ⎠
Der Abstand von P zu E ist 6.
240
289
7. a) 1
3
b) 1
c) 2
3
d) 7
e)
1
11
f)
1
5
1
G ⎛ ⎞
8. a) Der Normalenvektor n = ⎜ 1 ⎟ ist senkrecht zum Richtungsvektor:
⎜ −2 ⎟
⎝ ⎠
2
G ⎛ ⎞
n ⋅ ⎜1⎟ = 0 .
⎜ 3⎟
⎝ ⎠
Wähle z. B. P(3 | −1 | 2) ⇒ Abst(g; E) = Abst(P; E) = 5 3 ≈ 2,887
3
b) Der Richtungsvektor der Geraden ist eine Linearkombination der
Richtungsvektoren der Ebene:
⎛ 2 ⎞ ⎛ 1 ⎞ ⎛ −1⎞
⎜ −1⎟ = ⎜ 3 ⎟ − ⎜ 4 ⎟
⎜ 0 ⎟ ⎜ 2⎟ ⎜ 2 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
Gerade und Ebene sind parallel.
Wähle z. B. P(1 | −2 | 1) ⇒ Abst(g; E) = Abst(P; E) = 3
23
69 ≈ 1, 083
9. a) Die Normalenvektoren sind Vielfache voneinander:
JJG ⎛ 3 ⎞ JJG ⎛ −9 ⎞
JJG JJG
n1 = ⎜ −1⎟ ; n 2 = ⎜ 3 ⎟ ; − 3n1 = n 2 ⇒ Ebenen parallel.
⎜2⎟
⎜ −6 ⎟
⎝ ⎠
⎝ ⎠
Abst ( E1 ; E 2 ) = 14 ≈ 3, 742
b) Die Normalenvektoren sind Vielfache voneinander:
JJG ⎛ 1 ⎞ ⎛ −1⎞ ⎛ −2 ⎞ JJG ⎛ 2 ⎞
JJG JJG
n1 = ⎜ 1 ⎟ × ⎜ 2 ⎟ = ⎜ −4 ⎟ ; n 2 = ⎜ 4 ⎟ ; − n1 = n 2 ⇒ Ebenen parallel.
⎜ 2⎟ ⎜ 2 ⎟ ⎜ 3 ⎟
⎜ −3 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎝ ⎠
Abst ( E1 ; E 2 ) = 13 29 = 2, 414
29
c) Die Normalenvektoren sind Vielfache voneinander:
JJG ⎛ 1 ⎞ ⎛ −1⎞ ⎛ 2 ⎞ JJG ⎛ −3 ⎞ ⎛ 5 ⎞ ⎛ −2 ⎞
JJG JJG
n 1 = ⎜ 1 ⎟ × ⎜ 2 ⎟ = ⎜ 1 ⎟ ; n 2 = ⎜ 3 ⎟ × ⎜ −4 ⎟ = ⎜ − 1 ⎟ ; − n 1 = n 2
⎜ −1⎟ ⎜ 0 ⎟ ⎜ 3 ⎟
⎜ 1 ⎟ ⎜ 2 ⎟ ⎜ −3 ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⇒ Ebenen parallel.
Abst ( E1 ; E 2 ) = 9 14 ≈ 4,811
7
241
290
1
G ⎛ ⎞
10. a) n = ⎜ 2 ⎟ ⋅ 2 ; P(3 | 0 | 0)
⎜ −2 ⎟ 3
⎝ ⎠
⎡
⎛ 11 ⎞ ⎤
3
11 ⎞
1⎞ ⎢
⎛
⎛
JJJ
G
G
G
G ⎜ ⎟⎥
q = OP + n = 1 ⎜ 4 ⎟ ; E1: ⎜ 2 ⎟ ∗ ⎢ x − ⎜ 4 ⎟ ⎥ = 0
3⎜
⎟
⎜ −2 ⎟ ⎢
⎜ 34 ⎟ ⎥
⎝ −4 ⎠
⎝ ⎠ ⎢
⎜ − ⎟⎥
⎝ 3 ⎠⎦
⎣
⎡
⎛ 7 ⎞
⎛ 7 ⎞⎤
3
⎛ 1 ⎞ ⎢ G ⎜ 3 ⎟⎥
G JJJG G ⎜ 4 ⎟
r = OP + n = ⎜ − ⎟ ; E 2 : ⎜ 2 ⎟ ∗ ⎢ x − ⎜ − 4 ⎟ ⎥ = 0
⎜ −2 ⎟ ⎢
⎜ 43 ⎟
⎜ 43 ⎟ ⎥
⎝ ⎠ ⎢
⎜ ⎟
⎜ ⎟⎥
⎝ 3 ⎠
⎝ 3 ⎠⎦
⎣
b) E1: 6x1 − 3x 2 + 2x 3 = 21
E 2 : 6x1 − 3x 2 + 2x 3 = −7
c) E1: x1 + x 2 = 2 2
d) E1: x1 − 2x 3 = 3 + 2 5
E 2 : x1 + x 2 = −2 2
E 2 : x1 − 2x 3 = 3 − 2 5
JJJG ⎛ 2 ⎞ JJJG ⎛ 4 ⎞
11. a) AB = ⎜ 2 ⎟ ; AC = ⎜ 0 ⎟ sind offensichtlich linear unabhängig
⎜0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⇒ A, B, C definieren eine Ebene E: x1 − x 2 − 4x 3 + 30 = 0
b) Fehler in der 1. Auflage. Die Koordinate von P lautet: P(2 | 6 | 6,5).
• P liegt in E.
JJJG JJJG
JJJG
JJJG
• Es gilt z. B.: OP = OA + 1 ⋅ AB + 0,5 ⋅ BC und
JJJG JJJG
JJJG
JJJG
OP = OA + 1 ⋅ AC + 0,5 ⋅ CB, also P liegt auf der Seite BC.
Abst ( P, g AB ) : 1,5 (Bei B hat das Dreieck einen rechten Winkel.)
Abst ( P, g BC ) = 0; Abst ( P, g AC ) ≈ 1,138
12. Ist P der Fußpunkt des Lots von B auf die Gerade so gilt:
⎛ 3⎞
JJJG ⎛ 2 ⎞
OP = ⎜ 0 ⎟ + t ⋅ ⎜ 2 ⎟ .
⎜0⎟
⎜ 1⎟
⎝ ⎠
⎝ ⎠
⎡⎛ 2 ⎞ ⎛ 3 ⎞ ⎤ ⎛ 10 ⎞ JJJG
⎛ 3⎞
JJJG ⎛ −8 ⎞
BP = ⎜ −7,5 ⎟ + t ⋅ ⎜ 2 ⎟
Es gilt weiter: ⎢⎜ 0 ⎟ + t ⎜ 2 ⎟ ⎥ − ⎜ 7,5 ⎟ = BP
⎢⎜ ⎟ ⎜ ⎟ ⎥ ⎜
⎟
⎜ −0,3 ⎟
⎜ 1⎟
⎝
⎠
⎝ ⎠
⎣⎝ 0 ⎠ ⎝ 1⎠ ⎦ ⎝ 0,3 ⎠
JJJG ⎛ 3 ⎞
393
≈ 2,807
BP * ⎜ 2 ⎟ = 0 ⇔ − 39,3 + 14t = 0 ⇒ t = 140
⎜ 1⎟
⎝ ⎠
JJJG ⎛ 0, 4214 ⎞
JJJG
BP = ⎜ −1,8857 ⎟ , | BP | ≈ 3,165 km
⎜ 2,507 ⎟
⎝
⎠
242
290
13. a) Abst(P; g) = 3
b) Abst(P; g) ≈ 2,928
1
0
G ⎛ ⎞ ⎛ ⎞
c) g: x = ⎜ 1 ⎟ + t ⎜ 2 ⎟ ; Abst(P; g) = 3
⎜0⎟ ⎜ 2⎟
⎝ ⎠ ⎝ ⎠
−4
6
G ⎛ ⎞ ⎛ ⎞
d) g: x = ⎜ 2 ⎟ + t ⎜ −1 ⎟ ; Abst(P; g) ≈ 0,346
⎜ 1 ⎟ ⎜ 10 ⎟
⎝ ⎠ ⎝ ⎠
⎛2⎞
⎛ 4⎞
14. a) ⎜ −1⎟ = 1 ⎜ −2 ⎟ ⇒ Richtungsvektoren kollinear ⇒ parallele Geraden
⎜ 2 ⎟ 2⎜ 4 ⎟
⎝ ⎠
⎝ ⎠
Abst(g; h) = 5 26 ≈ 8, 498
3
⎛3⎞
⎛ −6 ⎞
b) ⎜ −3 ⎟ = − 1 ⎜ 6 ⎟ ⇒ parallele Geraden
2⎜
⎜4⎟
⎟
⎝ ⎠
⎝ −8 ⎠
Abst(g; h) ≈ 10,326
15. a) Abst(A; g) = 2 5
b) Ebene orthogonal zu g, die A enthält:
E: 2x1 + x 2 − x 3 − 2 = 0
Schnittpunkt mit g: F(2 | 1 | 3)
JJJG ⎛ 2 ⎞
JJJJG
JJJG ⎛ −2 ⎞
FA = ⎜ −4 ⎟ ⇒ FA ' = − FA = ⎜ 4 ⎟ ⇒ A’(0 | 5 | 3)
⎜ 0⎟
⎜ 0⎟
⎝ ⎠
⎝ ⎠
16. a) Wenn P ∈ g gelten soll, müssen die Gleichungen für die x1 - und die
x 3 - Koordinate für das gleiche t erfüllt sein:
für x1 : 8 = 4 + t
⇒t=4
für x 3 : 5 = −1 + t ⇒ t = 6
Aus diesem Widerspruch folgt, dass P ∉ g ist.
(
b) Lotfußpunkt F 1 (20 − p) 1 (2p − 7) 1 (5 − p)
3
JJG
Abst(P; g) = FP =
3
1
3
3
)
( p 2 + 14p + 55) = 5
⇒ p = −7 + 69 ≈ 1,31 oder p = −7 − 69 ≈ −15,31
243
290
⎛ 5 ⎞
⎛ −1 ⎞
17. a) a1 = 5, denn ⎜ −10 ⎟ = −5 ⎜ 2 ⎟
⎜ 15 ⎟
⎜ −3 ⎟
⎝
⎠
⎝ ⎠
Abst ( g; h 5 ) =
5
14
⎛ 5 ⎞ ⎛ −1 ⎞
b) ⎜ −2a ⎟ ⋅ ⎜ 2 ⎟ = −5 − 13a = 0 ⇒ a 2 = − 5
13
⎜ 3a ⎟ ⎜ −3 ⎟
⎝
⎠ ⎝ ⎠
Lösen der Vektorgleichung h a 2 = g nach t, r liefert Widerspruch
⇒ windschief
4.5.3 Winkel zwischen einer Geraden und einer Ebene
292
2. a) Der Winkel zwischen Bleistift und Buch, der kleiner ist als 90°, ist ein
sinnvoller Winkel. Ebenso der Winkel zwischen Bleistift und Lot.
b)
Nach Satz 5, S. 256 im Schülerband ist der Winkel zwischen zwei
G G G G
Vektoren n ∗ v = n ⋅ v ⋅ cos ϕ∗ .
Da ϕ = 90° − ϕ∗ und cos(90° − ϕ) = sin ϕ ist, folgt: sin ϕ =
G G
n∗v
G G
n⋅v
.
Um immer den kleineren Winkel zu berechnen, ist der Betrag des
G G
Skalarproduktes zu nehmen: sin ϕ = nG ∗ vG .
n⋅v
G
G
3. sin ϕ = nG ∗ vG
n⋅v
a) ϕ = 40,48°
b) ϕ = 35,26°
c) ϕ = 4,34°
d) ϕ = 2,84°
e) ϕ = 35,26°
f) ϕ = 32,31°
G G
4. Wegen n ∗ v = 0 liegt g entweder in E oder parallel zu E. Da (1 | 2 | 3) ∉ E,
liegt g parallel. Es existiert also kein Schnittwinkel.
244
292
JJJG ⎛ 4 ⎞ JJJG ⎛ 4 ⎞
5. Z. B. v R = ⎜ 3 ⎟ ; v G = ⎜ −3 ⎟
⎜ −5 ⎟
⎜ −5 ⎟
⎝ ⎠
⎝ ⎠
Gerade
Rot
Ebene
x 1x 2
45°
x 1x 3
25,1°
x 2x3
Grün
45°
25,1°
34,45°
6. a) Spurpunkte E1: S1
( 23
34,45°
)
0 0 ; S 2 (0 | −1 | 0); S3 (0 | 0 | 2)
Spurpunkte E 2 : S1 (0 | 0 | 0); S 2 (0 | 0 | 0); S3 (0 | 0 | 0)
Winkel
Ebene
Achse
x1
E1
E2
53,3°
24,1°
x2
32,31°
24,1°
x3
15,5°
54,74°
a
1
0
0
G ⎛ ⎞ JJJG ⎛ ⎞ JJJJG ⎛ ⎞ JJJJG ⎛ ⎞
b) n = ⎜ b ⎟ ; v x1 = ⎜ 0 ⎟ ; v x 2 = ⎜ 1 ⎟ ; v x 3 = ⎜ 0 ⎟
⎜c⎟
⎜0⎟
⎜ 0⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎝ ⎠
sin ϕ1 = aG ; sin ϕ 2 = bG ; sin ϕ3 = cG
n
n
G
n = a 2 + b2 + c2
( sin ϕ1 ) 2 + ( sin ϕ 2 ) 2 + ( sin ϕ3 ) 2
n
= G12 ( a 2 + b 2 + c 2 ) = 1
n
245
293
7. a) g liegt auf E
b) g liegt auf E
(
− 36
7
40
7
) , ϕ = 90°,
c) E: x1 + 2x2 − 3x3 = −28
S − 47
Projektion besteht nur aus S.
d) E: 5x1 − x2 − 3x3 = −3
S (2 | 1 | 4), ϕ ≈ 64,62°
S′
(
13
7
−
4
7
30
7
)
⎛ 2⎞
⎛ 1⎞
G
g′: x = ⎜ 1⎟ + t ⋅ ⎜ 11⎟
⎜ 4⎟
⎜ −2 ⎟
⎝ ⎠
⎝ ⎠
2
G ⎛ ⎞ G
8. n = ⎜ 3 ⎟ ; n = 15; sin(30°) = 1
2
⎜1⎟
⎝ ⎠
Der Richtungsvektor habe die Länge 1
⇒
1
2
=
2v1 + 3v 2 + v 3
15
; v12 + v 2 2 + v 3 2 = 1
JJG ⎛ 0,864 ⎞ JJG ⎛ 0, 778 ⎞
Beispiele für Richtungsvektoren: v1 = ⎜ 0,503 ⎟ ; v 2 = ⎜ 0 ⎟
⎜ 0 ⎟
⎜ 0, 628 ⎟
⎝
⎠
⎝
⎠
Beispiele für die Position des Lasers:
P1 = (21, 6 | 12,575 | 0); P2 (19, 45 | 0 | 15, 7)
(Alle möglichen Punkte bilden einen Kreis)
9. a) D(−6 | 3 | 2);
⎛ 2⎞ ⎛6⎞
G
Normalenvektor von E ABC mit Länge 9 n = 3 ⋅ ⎜ 2 ⎟ = ⎜ 6 ⎟ ;
⎜ 1⎟ ⎜ 3⎟
⎝ ⎠ ⎝ ⎠
JJJG JJJJG G
Mittelpunkt von ABCD: M(−3 | 0 | 2) ⇒ OS = OM ± n
⇒ S(3 | 6 | 5) oder S(−9 | −6 | −1)
Da S oberhalb von x1x 2 -Ebene, ist die Lösung S(3 | 6 | 5).
JJJG ⎛ −7 ⎞ JJG ⎛ −3 ⎞
b) SA = ⎜ −7 ⎟ ; SB = ⎜ −9 ⎟ ; sin ϕ =
⎜ 1⎟
⎜ −3 ⎟
⎝ ⎠
⎝ ⎠
9
11
⇒ ϕ ≈ 54,9°
JJJJJG ⎛ 5 ⎞
c) Normalenvektor der Seite ABS: n ABS = ⎜ −4 ⎟
⎜7⎟
⎝ ⎠
Winkel zwischen 2 Ebenen cos α =
G JJJJJG
n ∗ n ABS
G JJJJJG
n ⋅ n ABS
⇒ α ≈ 71,6°
246
293
10. a) Mastspitze M(2 | 1 | 9)
2
⎛1⎞
G ⎛ ⎞
Gerade der Sonnenstrahlen g: x = ⎜ 1 ⎟ + r ⎜ −2 ⎟
⎜9⎟
⎜ −2 ⎟
⎝ ⎠
⎝ ⎠
Schnittpunkt von g mit E: S1
(
54
11
− 53 35
11
11
)
1
G G
G ⎛ ⎞
Winkel zwischen g und E: n = ⎜ 2 ⎟ ; sin ϕ1 = nG ∗ uG ⇒ ϕ1 ≈ 53,14°
n ⋅ u
⎜ 4⎟
⎝ ⎠
1
G ⎛ ⎞
b) Richtungsvektor des Seils: n = ⎜ 2 ⎟
⎜ 4⎟
⎝ ⎠
Befestigungspunkt (2 | 1 | 3)
2
⎛1⎞
G ⎛ ⎞
Gerade des Seils g S : x = ⎜ 1 ⎟ + s ⎜ 2 ⎟
⎜ 3⎟
⎜ 4⎟
⎝ ⎠
⎝ ⎠
Schnittpunkt g S mit E: S 2
(
34
21
5
21
31
21
)
JJJG ⎛ 0 ⎞
Winkel zwischen g S und Mast: n M = ⎜ 0 ⎟
⎜1⎟
⎝ ⎠
sin ϕ 2 =
JJJG G
nM ∗ n
JJJG G
nM ⋅ n
⇒ ϕ 2 ≈ 60, 79°
4.5.4 Winkel zwischen zwei Ebenen
295
1. a) cos (ϕ) = 13 ϕ ≈ 70,53°
b) cos (ϕ) = 21 ϕ = 60°
JJG JJG
c) n1 * n2 = 0 ⇒ ϕ = 90°
JJG ⎛ 4 ⎞
126
d) n2 = ⎜ −5 ⎟ ⇒ cos(ϕ) = 63
ϕ ≈ 79,74°
⎜ −1⎟
⎝ ⎠
JJG ⎛ 9 ⎞
e) n2 = ⎜ 4 ⎟ ⇒ cos(ϕ) = 4 ⋅ 73292
ϕ ≈ 20,56°
⎜ −7 ⎟
⎝ ⎠
JJG ⎛ 1⎞ JJG ⎛ 7 ⎞
f) n1 = ⎜ −2 ⎟ , n2 = ⎜ −5 ⎟ ⇒ cos(ϕ) = 7 6060
ϕ ≈ 25,35°
⎜ −1⎟
⎜ −4 ⎟
⎝ ⎠
⎝ ⎠
247
295
JJG ⎛ 4 ⎞
1. g) n1 = ⎜ 5 ⎟ ,
⎜ 1⎟
⎝ ⎠
JJG ⎛ 2 ⎞
h) n1 = ⎜ 2 ⎟ ,
⎜ 1⎟
⎝ ⎠
JJG ⎛ 1⎞
n2 = ⎜ −2 ⎟ ⇒ cos(ϕ) =
⎜ 0⎟
⎝ ⎠
−6
210
ϕ ≈ 65,54°
JJG ⎛ −4 ⎞
n 2 = ⎜ 11 ⎟ ⇒ cos(ϕ) =
⎜ 5⎟
⎝ ⎠
19
27 2
ϕ ≈ 60,16°
2. Koordinatenebenen Normalenvektoren
JJJG ⎛ 0 ⎞
x1x 2 -Ebene n12 = ⎜ 0 ⎟ ⇒ Winkel ϕ1
⎜1⎟
⎝ ⎠
0⎞
⎛
JJJG
x1x 3 -Ebene n13 = ⎜ 1 ⎟ ⇒ Winkel ϕ 2
⎜0⎟
⎝ ⎠
JJJG ⎛ 1 ⎞
x 2 x 3 -Ebene n13 = ⎜ 0 ⎟ ⇒ Winkel ϕ3
⎜0⎟
⎝ ⎠
1
G ⎛ ⎞
a) n = ⎜ −1 ⎟ ;
cos ϕ1 = 2 ; ϕ1 ≈ 35, 26°
3
⎜ −2 ⎟
⎝ ⎠
cos ϕ 2 =
1
;
6
ϕ 2 ≈ 60,91°
cos ϕ3 = 1 ; ϕ3 ≈ 60,91°
6
Spurpunkte S1 (6 | 0 | 0); S 2 (0 | −6 | 0); S3 (0 | 0 | −3)
248
295
1
G ⎛ ⎞
2. b) n = ⎜ −3 ⎟ ;
⎜5⎟
⎝ ⎠
cos ϕ1 =
5
;
7
cos ϕ 2 =
3
;
35
ϕ1 ≈ 32,31°
ϕ 2 ≈ 59,53°
cos ϕ3 = 1 ; ϕ3 ≈ 80, 27°
35
E: x1 − 3x 2 + 5x 3 = 4
(
)
(
S1 (4 | 0 | 0); S 2 0 | − 4 | 0 ; S3 0 | 0 | 4
1
G ⎛ ⎞
c) n = ⎜ 3 ⎟ ;
⎜ −4 ⎟
⎝ ⎠
3
cos ϕ1 = 2
2;
13
5
)
ϕ1 ≈ 38,33°
cos ϕ 2 =
3
;
26
ϕ 2 ≈ 53,96°
cos ϕ3 =
1
;
26
ϕ3 ≈ 78, 69°
S1 (12 | 0 | 0); S 2 (0 | 4 | 0); S3 (0 | 0 | −3)
249
295
1
G ⎛ ⎞
2. d) n = ⎜ 3 ⎟ ;
⎜0⎟
⎝ ⎠
cos ϕ1 = 0; ϕ1 = 90°
3
;
10
cos ϕ 2 =
ϕ 2 ≈ 18, 43°
cos ϕ3 = 1 ; ϕ3 ≈ 80, 27°
10
E: x1 + 3x 2 = 6
S1 (6 | 0 | 0); S 2 (0 | 2 | 0); S3 existiert nicht
3. a) S(4 | 4 | 10); A(8 | 0 | 0); B(8 | 8 | 0); C(0 | 8 | 0)
JJG ⎛ 3 ⎞
JJG ⎛ 6 ⎞
Normalenvektor SAB: n1 = ⎜ 2 ⎟ ; Normalenvektor SBC: n 2 = ⎜ 4 ⎟
⎜ 2⎟
⎜1⎟
⎝ ⎠
⎝ ⎠
cos ϕ =
28
901
⇒ ϕ ≈ 21,12°
Da die Figur symmetrisch ist, gilt dies für alle Winkel zwischen
Seitenflächen.
b) Schnittpunkte von E mit Kanten der Pyramide:
(
S1 (6 | 2 | 5); S 2 7 | 7
5
2
) ; S (3 | 5 ) ; S (
3
Schnittfläche ist Viereck mit A =
15
2
1d
2 1
4
22
7
22
7
55
7
⋅ d 2 ⋅ sin α .
Länge der Diagonalen d1 ≈ 4,92; d 2 ≈ 7, 65;
Schnittwinkel der Diagonalen α ≈ 69,16° ⇒ A ≈ 17,59
JJJG ⎛ −4 ⎞ G ⎛ 20 ⎞
c) AS = ⎜ 4 ⎟ ; n = ⎜ 5 ⎟ ⇒ sin ϕ ≈ 0,382 ⇒ ϕ ≈ 22, 44°
⎜ 10 ⎟
⎜ 18 ⎟
⎝ ⎠
⎝ ⎠
)
250
295
JJJJJJG ⎛ 1 ⎞ JJJJJJG ⎛ 0 ⎞
4. a) n PQR = ⎜ 1 ⎟ ; n BCG = ⎜ 1 ⎟ ⇒ cos ϕSeite = 1 ⇒ ϕSeite ≈ 72, 45°.
11
⎜ 3⎟
⎜0⎟
⎝ ⎠
⎝ ⎠
JJJJJJG ⎛ 0 ⎞
n EGH = ⎜ 0 ⎟ ⇒ cos ϕ Deck = 3 ⇒ ϕ Deck = 25, 24°.
11
⎜1⎟
⎝ ⎠
JJJG JJJG JJJG
b) V = VWürfel − VPyramide = 4 3 − 1 ( PQ × QR ) ∗ QF = 64 − 3 = 62,5
6
2
JJJG JJJG
3
1
c) A = QP × QR =
11 ≈ 4,975
2
2
JJG ⎛ 1 ⎞
5. Normalenvektor der Ebene, die A, B, C enthält n1 = ⎜ 1 ⎟ .
⎜ −1⎟
⎝ ⎠
JJG ⎛ −1⎞
Normalenvektor der Ebene, die B, C, D enthält n 2 = ⎜ 1 ⎟ .
⎜1⎟
⎝ ⎠
Winkel ϕ zwischen den Ebenen: cos ϕ =
296
6. a) Dachneigung: tan α
JJJG
A ABQP = 1 BQ +
2
JJJG
A PQCD = 1 QC +
(
(
2
JJG JJG
n1 ∗ n 2
JJG JJG
n1 ⋅ n 2
=
1
3
⇒ ϕ ≈ 70,5°
Dachhöhe
=
= 3 m ⇒ α ≈ 36,87°
Grundmaß bis First
4m
JJJG
JJJG
1
AP ∗ AB = (12 + 16) ⋅ 5 = 70 m 2
2
JJJG
JJJG
PD ∗ CD = 55 m 2
)
)
Normalenvektoren:
JJJJJJJG ⎛ 0 ⎞
JJJG JJJG
(
n ABQP = ⎜ 3 ⎟
proportional zu AB × BQ )
⎜ 4⎟
⎝ ⎠
JJJJJJJG ⎛ 3 ⎞
JJJG JJJG
(
n PQCD = ⎜ 0 ⎟
proportional zu CQ × CD )
⎜ 4⎟
⎝ ⎠
⇒ cos ϕ =
JJJJJJJG JJJJJJJG
n ABQP ⋅ n PQCD
JJJJJJJG JJJJJJJG
n ABQP ⋅ n PQCD
=
16
25
⇒ ϕ = 50, 2°
⎛4⎞
JJJG
b) PQ = ⎜ 4 ⎟ = 41 ≈ 6, 403 m
⎜ −3 ⎟
⎝ ⎠
c) Schornsteinspitze S(3 | 10 | 7,75); Dachebene E: 3x1 + 4x 3 − 32 = 0
Hessesche Normalenform
1
5
( 3x1 + 4x 3 − 32 ) = 0 ⇒ Abst (S; E) = 1,6 m
251
296
7. a) C(−3 | 5 | 0); D(−3 | −5 | 0); G(−2 | 3 | 3); H(−2 | −3 | 3)
Zeichnung: siehe Schülerbuch.
Neigungswinkel = Winkel zwischen Seitenfläche und x1x 2 -Ebene
JJG ⎛ 0 ⎞
mit n1 = ⎜ 0 ⎟
⎜1⎟
⎝ ⎠
Normalenvektoren der Seitenflächen:
JJJJJJJG ⎛ 3 ⎞ JJJJJJJG ⎛ 0 ⎞
n ABEF = ⎜ 0 ⎟ ; n BCFG = ⎜ 3 ⎟
⎜1⎟
⎜ 2⎟
⎝ ⎠
⎝ ⎠
Neigungswinkel ABEF und CDGH:
cos ϕ1 =
JJJJJJJG JJG
n ABEF ∗ n1
JJJJJJJG JJG
n ABEF ⋅ n1
=
1 ;
10
ϕ1 ≈ 71, 6°.
Neigungswinkel BCFG und ADEH; cos ϕ 2 =
2
;
13
ϕ 2 ≈ 56,3°.
b) Der Mast ragt durch die Fläche BCFG, die in der Ebene
E: 3x 2 + 2x 3 − 15 = 0 liegt. Abst(E; P) =
3
13
≈ 0,832
⇒ Der Mast ragt (5 − 0,832) m = 4,168 m heraus.
Mitte des Mastes M(0 | 4 | 2,5); Abst(E; M) = 0,555 m
Das Seil ist 55,5 cm lang.
8. a)
Böschungswinkel: tan α =
47,04 m
1
2
(189,43 m −123,58 m )
=
47,04
32,925
α = 55,01° = 55°0’36’’
Mit den Längenangaben ist der Böschungswinkel etwas größer als der
im Internet angegebene.
Innenwinkel γ = 168,014° = 168°0’50’’
b) h P = tan α ⋅ 1 (189, 43 m) = 135,32 m
2