Test 1 (Vektorgeometrie) 19. März 2008 Aufgabe 1 Die 4 Punkte A(4

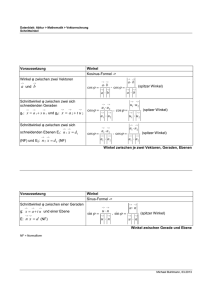
Test 1 (Vektorgeometrie)
19. März 2008
Aufgabe 1 Die 4 Punkte
A(4, 0, 3),
B(8, −6, 11),
C(6, 5, 0),
D(−2, 1, −2)
liegen in der gleichen Ebene.
(a) Bestimmen Sie den Schnittpunkt der Geraden (AB) und (CD).
(2 Punkte)
(b) Bestimmen Sie den spitzen Winkel zwischen den beiden Geraden.
(2 Punkte)
(c) Bestimmen Sie die Koordinatengleichung der Ebene, in welcher die beiden Geraden liegen.
(2 Punkte)
Aufgabe 2 Gegeben sei ein Tetraeder mit den 4 Ecken
A(2, 3, 1),
B(4, 1, −2),
C(6, 3, 7),
D(−5, −4, 8) .
(a) Bestimmen Sie die Länge der Höhe, die von der Ecke D auf die gegenüberliegende
Seitenfläche gefällt wird.
(2 Punkte)
(b) Bestimmen Sie den spitzen Winkel, den die Seitenflächen (ABC) und (ABD)
bilden.
(2 Punkte)
Aufgabe 3 Geben Sie einen Einheitsnormalenvektor der Ebene 2x − y + 5z − 12 = 0
an.
(1 Punkt)
Lösungen zum Test 1 (Vektorgeometrie)
Aufgabe 1
19. März 2008
(a) Die Parametergleichungen der beiden Geraden lauten :
 


 


4
4
6
−8
!r1 =  0  + t  −6  und !r2 =  5  + s  −4 
3
8
0
−2
Um den Schnittpunkt zu finden, müssen wir die rechten Seiten gleichsetzen :
 

  


4
4
6
−8
 0  + t  −6  =  5  + s  −4 
3
8
0
−2
Wir erhalten das lineare Gleichungssystem :
4t + 8s = 2
−6t + 4s = 5
8t + 2s = −3
Wir subtrahieren das Doppelte der zweiten Gleichung von der ersten :
16t = −8 =⇒ t = −
1
2
Wir finden s = 12 . Wir müssen überprüfen, dass alle 3 Gleichgungen erfüllt sind,
weil nur dann ein Schnittpunkt vorliegt ! Die beiden Werte erfüllen in der Tat alle
3 Gleichungen. Der Schnittpunkt ist gegeben durch S(2, 3, −1) .
−−→
−−→
(b) Wir bestimmen den Winkel zwischen den Vektoren AB und CD.




4
−8
−−→ 
−−→
−6  und CD =  −4 
AB =
8
−2
Wir berechnen das Skalarprodukt auf zwei Arten :
−−→ −−→
AB · CD = −32 + 24 − 16 = −24
√
√
√
−−→ −−→
−−→ −−→
AB · CD = |AB| · |CD| cos γ = 116 · 84 cos γ = 4 609 cos γ
Gleichsetzen und nach cos γ auflösen :
−24
6
.
.
cos γ = √
= −√
= −0.243132 =⇒ γ = 104.1o
4 609
609
Der spitze Winkel ist also 75.9o .
(c) Der Vektor




44
11
−−→ −−→ 
−56  = 4  −14 
AB × CD =
−64
−16
ist ein Normalenvektor der gesuchten Ebene. Also lautet die Koordinatengleichung :
11x − 14y − 16z + D = 0
Wir bestimmen D , indem wir die Koordinaten des Punkts A einsetzen :
44 − 48 + D = 0 =⇒ D = 4
Also lautet die gesuchte Gleichung :
11x − 14y − 16z + 4 = 0
Aufgabe 2
(a) Wir berechnen zuerst die Vektoren :


 
2
4
−−→
−→
!a = AB =  −2  , !b = AC =  0  ,
−3
6


−7
−−→
!c = AD =  −7 
7
Die Länge der Höhe durch D ist gleich dem Abstand d des Punktes D von der
Ebene (ABC). Dafür haben wir die folgende Formel :
d=
[!a, !b, !c]
|!a × !b|
Es gilt :
%
% 4 −7
2
%
[!a, !b, !c] = [!b, !c, !a] = %% 0 −7 −2
% 6
7 −3
Weiter gilt :

%
%
%
%
%
% = 4 % −7 −2
%
% 7 −3
%
%
%
%
%
2
% + 6 % −7
%
% −7 −2

−12
%
%
%
%
!a × !b =  −24  =⇒ %!a × !b% = 28
8
Also ist der gesuchte Abstand d = 308/28 = 11 .
(b) Wir berechnen die Normalenvektoren dieser Seitenflächen :




−3
−5
!a × !b = 4  −6  und !a × !c = 7  1 
2
−4
Wir berechnen jetzt den Winkel zwischen den Vektoren




−3
−5
!n1 =  −6  und !n2 =  1 
2
−4
Wir berechnen wiederum auf 2 Arten das Skalarprodukt :
!n1 · !n2 = 15 − 6 − 8 = 1
√
!n1 · !n2 = |!n1 | · |!n2 | cos α = 7 42 cos α
Der Winkel ist gegeben durch :
1
.
cos α = √ = 0.0220433 =⇒ α = 88.7o
7 42
Aufgabe 3


2
1 
−1 
!n = √
30
5
%
%
% = 308
%