Skript §12

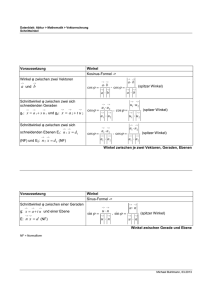
Geometrie
Oberstufe
Seite 23
§12. Winkel
1. Wiederholung


Der Zwischenwinkel  zweier Vektoren a und b errechnet sich nach der Formel:
 

ab

cos  
mit a = | a | und b = | b | (vgl. §05)
a b
Setzt man die Richtungsvektoren zweier Geraden in diese Formel ein, so erhält man den
Schnittwinkel der beiden Geraden. Dabei ist zu beachten, dass mn immer denjenigen Winkel
verwendet der zwischen 0° und 90° liegt, also für den der cos größer oder gleich Null ist:
cos  
u1 u 2
u1  u 2
mit u1 = | u1 | und u2 = | u 2 |
Mit der NF einer Ebene können nun auch Zwischenwinkel zweier Ebenen oder einer
Ebene/Gerade bestimmt werden.
2. Winkel zwischen zwei Ebenen E und F

 
E: n1  (x  a )  0 (NF)

 
F: n 2  (x  b)  0 (NF)
Der Zwischenwinkel von E und F ist so groß
wie der Zwischenwinkel der beiden Normalen

vektoren n1 und n 2
Also setzt man diese in die Formel ein und erhält für den Zwischenwinkel  zweier Ebenen:
cos  
n1 n 2
n1  n 2


mit n1 = | n1 | und n2 = | n 2 |
3. Winkel zwischen einer Gerade g und einer Ebene E
  
E: n  (x  a )  0 (NF)
 

g: x  a  u

Verwendet man den Normalenvektor n der Ebene und

den Richtungsvektor u der Gerade, so stellt man fest
dass der Winkel * zwischen diesen n i c h t der
Winkel zwischen Ebene und Gerade ist. Der gesuchte
Winkel  und * ergänzen sich jedoch zu 90°.
Also gilt: * = 90°–.
Außerdem ist cos * = cos(90°–) = sin 
und man kann somit den Winkel  zwischen Gerade und Ebene mit folgender Formel bestim–
men:
sin  
n u
nu
© H. Drothler 2012


mit n = | n | und u = | u |
www.drothler.net