Folien zur 9. Vorlesung
Werbung

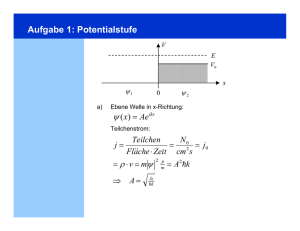
Experimentalphysik III Experimentelle Grundlagen der Quantenphysik Frank Cichos Vorlesung 9 Linienspektren - Balmer Serie 1.5.3. Bohr‘s model Emission spectrum of a hydrogen atom Balmer‘s formula m2 " = 364.6nm 2 m #4 Brackett Pfund ! more common form: Rydberg - Ritz formula (1908) = Ry 1 m2 1 n2 Balmer n=1 n=2 n=3 n=4 ⇥ n, m are principle numbers n defines the series Lyman wavelength Lyman Balmer Paschen Brackett excitation energy in eV Paschen Bohrsches Atommodell 1.5.3. Bohr‘s model Nils Bohr (1913) • electron is in circular orbit around positive charge electron Coulomb centrifugal v Ze2 r= 4⇥ µv 2 in principle any radius is allowed proton • Bohr‘s hypothesis • angular momentum is quantized |L| = µrv = n • orbits are stable, no radiation (we‘ll see later that this corresponds to the idea of a standing electron wave and to de Broglie‘s idea) Bohrsches Atommodell 1.5.3. Bohr‘s model summary of Bohrs model of the hydrogen atom • electron moves on circles around the nucleus with quantized radii n2 rn = 2 a0 Z with a0 = 0h 2 ⇥µe2 • radii increase quadratically with n • possible values are inversely proportional to Ze, He+ is smaller than H • each state has a well defined total energy (approaches 0 for r"!) energies are negative, since bound En = Z2 Ry 2 n Epot = +2En Ekin = En • the energy E1 is needed to ionize the atom • by absorption of h#, the atom can be excited from Ei to Ek Bohrsches Atommodell Schwächen 1.5.3. Bohr‘s model weaknesses of Bohr‘s model • accelerated charges do radiate light this means they lose energy and will finally crash into the positive charge, not compatible with classical electrodynamics • lowest orbit has |L|=$ but experimentally one observes |L|=0 • orbital momentum is actually |L| = l(l + 1) • Zeeman effect, fine structure, hyperfine structure (but we do not know about this, yet) Franck Hertz Versuch (1911-1914) 1.5.3. Bohr‘s model Franck-Hertz experiment electrons loose energy in collisions e (Ekin ) + Hg ⇥ Hg ⇥ (Ea ) + e (Ekin • atoms can acquire only discrete energy quanta • the magnitude depends on the specific atom Ea ) electron current as function of the acc. voltage for mercury vapor Franck-Hertz Versuch Bessere Auflösung Linienspektren 1.5.3. Bohr‘s model atomic spectra (1859/1885, Balmer, Kirchhoff, Bunsen) • elements emit light of certain frequencies only • each element has a characteristic emission and absorption spectrum • spectral lines are not completely narrow emission spectrum of magnesium emission spectrum of silicon Bohr Sommerfeld Modell n … Hauptquantenzahl l … Drehimpulsquantenzahl 2. Einführung in die Quantenmechanik 2.1. Die Schrödingergleichung 2.2. Anwendungen der Schrödingergleichung Potentialstufe ur dort von null edingung genauer zu deWellen (4.11) Ep(x) D ⋅ eikx Ekin > E0 E0 A ⋅ eikx Ep = E 0 B ⋅ e−ikx Ekin < E0 I II 0 x Abb. 4.3. Eindimensionale Potentialbarriere Grenzfläche Vakuum-Materie (z. B. eine Glasoberflä- Potentialstufe 4.2. Anwendungsbeispiele der stationären Schrödingergleichung enzierbar sein, weil sonst die zweite x 2 nicht definiert und damit die ng nicht anwendbar wäre. Dies erd (4.14) die Randbedingungen für (x = 0) + B = C+ D, " ψII x 0 (A − B) = α (C − D) . E0−Ekin e (4.15a) (4.15b) nun die beiden Fälle, dass die Enerinlaufenden Teilchens kleiner oder ntialstufe ist (Abb. 4.3): – αx E0 A B Ekin 128 127 A =B x 0 4.Abb. Grundlagen der Quantenmechanik 4.4. Wellenfunktion ψ(x) bei vollständiger Reflexion der einlaufenden Welle für E kin < E 0 trotz Eindringens in das Gebiet mit 2π 2π E 0 > E kin λ= λ' = k k' Die Wahrscheinlichkeit W(x), ein Teilchen am Ort x > 0 zu finden, ist 2 # # 4k 2 −2α x |A| W(x) = |ψII | 2 = # D · e−α x # 2 = 2 e 2 2 2 α + k v⋅ A v'⋅ D 2 4k 2 −2α x , (4.19) E > E0 = 2 |A| e E0 k0 2 v⋅B α reell, und der Koeffizient C in wobei k 2 = 2m E /!2 ist. Nach einer Strecke x = 0 0 in, weil sonst ψII (x) für x → +∞ 1/(2α) ist die Eindringwahrscheinlichkeit auf 1/ex d damit nicht mehr normierbar. Aus ihres Wertes bei x = 0 abgesunken. 0 dann Abb. Dies 4.5. Transmission Reflexion für E >wohlvertraut. E0 ist uns ausundder Wellenoptik in das Reflexionsvermögen $ $ $ n 1 − n 2 $2 $ R = $$ n1 + n2 $ einer Lichtwelle umformen, die fläche zwischen zwei Medien m trifft (siehe Bd. 2, Abschn. 8.4.4 Um den Bruchteil aller pro tierten Teilchen (d. h. die Zah durch die Fläche x = x 0 > 0 g teilt durch die pro Zeiteinhe rgie auf E kin = E − E 0 ieht das im Wellenmob) ist nun rein imaginär, le Größe nis der Wellenzahlen bestimmt. Deshalb wird der Transmissionskoeffizient v′ |D|2 4k · k ′ T= = . 2 ′ 2 v|A| (k + k ) Reflexion an einer Potentialstufe (4.20) (4.24b) ebiet II heißen dann: (4.21) R 1 R ie −x-Richtung fließen, ik′ x lten ψII = D · e . Aus olgt: 2k A ′ k+k on # · e−ikx , 0,8 (4.22) 1,0 0,6 0,4 0,5 0,2 (4.23) d. h. der Bruchteil aldann analog zur Optik 4.4) –40 a) (4.24a) –30 –20 E 0/ E 0,5 0 b) –10 E 0/ E 0 0 0 1 Energie E pot (x) = E 0 ist. Das gesamte x-Gebiet wird nun in drei Bereiche I, II und III aufgeteilt, für die wir, aus den Überlegungen des vorigen Abschnitts, die Wellenfunktionen Tunneleffekt ψI = A eikx + B e−ikx , ψII = C eα x + D e−α x , ψIII = A′ eikx λ= (4.25) 2π k λ= E0 a I II 0 2π k III a x Abb. 4.7. Zum Tunneleffekt durch eine rechteckige Potentialbarriere 16E T ≈ 2 (E E0 Die Transmissio durch sie darge albarriere hängt rierehöhe E 0 , v Differenz ∆E = Im klassisch riere für E < E Durchdringung mechanischen B weil die Teilch diagramm auf Tunnel den Pot Potentialbarriere E pot (x) haben ( spielen jedoch d sie einfacher zu und Transmissiosvermögen T als Funktion des Verhältnisses E/E 0 dargestellt für den speziellen Fall einer rechteckigen Barriere mit der Breite a = 3λD (E 0 ), die Tunneln durch eine Potentialbarriere 1,0 R und T T ferenzersch den beiden tierten Ant von de Bro Teilchens o riere ab. Mi aus (4.27c) ⇒ λ′ = 2a/ 1 0,5 E − E0 R E20 (E −E0 ) + 4 ⋅E 0 0 1 5 10 E / E 0 0 Teilchens oberhalb der Barriere zur Dicke a der Bar√ riere ab. Mit k ′ = 2π/λ′ = 2m(E − E 0 )/! erhält man aus (4.27c) Maxima der Transmission für k ′ · a = n · π Streuung an einer Potentialbarriere ′ ⇒ λ = 2a/n (Abb. 4.10). Dann ist der Wegunterschied T 1 E − E0 E20 (E −E0 ) + 4 ⋅E E/E0 nsverBreite sener- 0 0,5 1 a/λ' Abb. 4.10. Transmissionsvermögen T als Funktion des Verhältnisses a/λ′ von Potentialbarrierenbreite a und de Broglie′ s Tunneleffektes ist das Tunnelmikroskop. Abstand G. Binnig H. Rohrer kroskop rekten Anwendungen des Tunneleffektes ist das Tunnelmikroskop. 1986 durch Vakuum itze und leitender Fläche Prinzipieller Aufbau eines STM s Tunnelstroms auf den Abstand (scanning tunneling microscope) brasterung einer Probe G.Leiden Binnig Univ.] H. Rohrer [Interf. Phys. Group, STM scope) en Univ.] Energiebänder für Spitze und Pr (rechts) angelegter Spannung [In Univ.] Energiebänder für Spitze und Probe ohne (links) und mit (rechts) angelegter Spannung [Interf. Phys. Group, Leiden Univ.] Bei einem typischen Wert von V=4eV folgt eine Erhöhung des Tunnelstroms um einen Faktor 1000 bei einer Abstandsänderung von nur 0.3 nm! Dies macht STM so empfindlich! Strom-Abstands-Kennlinie STM erfordert eine genaue Positionierung der STM-Spitze (Å-Präzision). Zu diesem Zweck werden piezoelektische Elemente eingesetzt. Feedback-Loop im STM Piezoelektrika: Prinzip und 3D-Scanner [alle Bilder: Interf. Phys. Group, Leiden Univ.] 2 Scanning Tunnelin Microscopy (STM) Bilder Beispiel einiger STM Bilder: Atomic Corral [IBM Gallery] Linescan und Bild von Graphit [Interf. Phys. Group, Leiden Univ.] 243 2.4.2. Der -Zerfall Beim -Zerfalls ergibt sich das Gesamtpotential aus der sehr kurzreichweitigen Tunneln beim α-Zerfall attraktiven Kernkraft und der repulsiven Coulombkraft zwischen den positiv geladenen -Teilchen, d.h He-Kernen (Rutherford 1908). E VCoulomb r starke Kernkraft Tunneleffekt 0 2.4.2. Der -Zerfall Atomkern Ladung Ze r VKern ergibt sich das Gesamtpotential aus der sehr kurzreichweitigen Beim -Zerfalls Vtot Coulombkraft zwischen den positiv geladenen attraktiven Kernkraft und der repulsiven -Teilchen, d.h He-Kernen (Rutherford 1908). E VCoulomb r starke Kernkraft Tunneleffekt Atomkern Ladung Ze