Quantenmechanik - Institut für Experimentelle Kernphysik

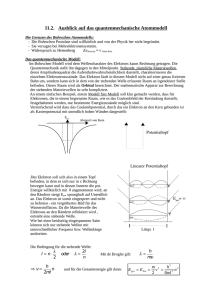
9. Übungsblatt
Universität Karlsruhe
Institut für Experimentelle Kernphysik
Ausgewählte Kapitel der Physik
SS 2007
Prof. Dr. G. Quast
Ausgabe: 27.06.2007
Besprechung: 05.07.2007
Dr. T. Kuhr
[email protected]
Quantenmechanik
Aufgabe 1: Potentialstufe
Ein Teilchenstrom der Stärke von N0 Teilchen pro Sekunde und cm2 in x-Richtung, bestehend aus Teilchen der Energie E und Masse m, trifft bei der Position x = 0 auf eine
Potentialstufe der Höhe V0 < E.
a) Ein solcher Teilchenstrahl kann in guter Näherung als ebene Welle beschrieben werden. Geben Sie die Gleichung für die ensprechende ebene Welle an. Wie ist die Normierungskonstante zu wählen?
Hilfe: Ein Strom ist gegeben durch das Produkt aus Teilchendichte und Teilchengeschwindigkeit. j = ρ · v.
b) Was passiert in der klassischen Physik mit dem Teilchenstrahl, d.h. was sind die
Teilchengeschwindigkeiten und Ströme rechts und links von der Potentialstufe?
c) Um das korrekte, quantenmechanisch bestimmte Verhalten des Teilchenstrahls zu
berechnen, kann man die eindimensionale, stationäre Schrödingergleichung benutzen.
Berechnen Sie zunächst den Reflexionskoeffizienten, d.h. den Quotienten aus einlaufendem und reflektiertem Teilchenstrom.
Hilfe: Formulieren Sie einen geeigneten Lösungsansatz für die Wellenfunktion für die
Gebiete rechts und links der Potentialstufe. Welche Bedingungen sind an die Wellenfunktion bei x = 0 zu stellen, um die freien Koeffizienten im Lösungsansatz zu
bestimmen?
d) Bestimmen Sie den Transmissions-Koeffizienten, d.h. den Quotienten der Teilchenströme vor und hinter der Potentialstufe.
e) Vergleichen Sie die quantenmechanische Lösung mit der klassischen! Unter welchen
Grenzbedingungen stimmen klassische und quantenmechanische Lösung überein?
Aufgabe 2: Potentialbarriere und Tunneleffekt
Ein Elektron befindet sich in einem Potentialkasten, der bei x = 0 durch eine unendlich hohe Wand begrenzt ist, und bei
x > 1.0 · 10−10 m durch eine Potentialbarriere mit der Dicke a = 0.1 nm und der
Höhe V0 = 1000 eV (siehe Skizze).
V=
8
V(x)
V0
a
0
1
−10
10
x
a) Skizzieren Sie den Verlauf der Wellenfunktion, wenn sich das Elektron im Potentialkasten im Grudzustand befindet. Nehmen Sie hierfür an, dass die Potentialbarriere
so hoch ist, dass sich Wellenfunktion und Energie des Elektrons nur wenig von denen
im Kastenpotential (Blatt 8, Aufg. 4) unterscheidet.
b) Berechnen Sie näherungsweise den Transmissionskoeffizienten T für die Transmission
eines Elektrons im Grundzustand durch die Potentialbarriere. Hinweis: Nehmen Sie
an, daß man die Wellenfunktion des Elektrons als Überlagerung einer nach links und
nach rechts laufenden Welle auffassen kann, die durch die Barriere tunnelt.
c) Das Elektron wird nach einer gewissen Zeit aus dem Potentialkasten wegtunneln.
Man kannn das folgendermassen verstehen: Das Elektron bewegt sich mit einer der
Grundzustandsenergie entsprechenden Geschwindigkeit zwischen der rechten und der
linken Seite periodisch hin und her. Berechnen Sie die dafür benötigte Zeit tu . Wie
groß ist die Transmissionsrate pro Umlauf, d.h. T /tu ? Wie groß ist deren Kehrwert,
d.h. tu /T ?
Hinweis: tu /T ist die “Zerfallszeit” des Elektrons im Potentialtopf. Die Änderung der
Wahrscheinlichkeit Pe , das Elektron nach einer Zeit ∆t noch im Kasten zu finden,
ist gegeben durch ∆Pe = −∆t tTu · P (t), oder, als Differentialgleichung geschrieben:
dPe
dt
=
T
tu
t
· P ; diese hat die Lösung P (t) = e− τ mit τ =
tu
T .
Aufgabe 3: Bohr’sches Atommodell und Wasserstoff (alte Klausuraufgabe)
Im Bohr’schen Modell des Wasserstoffatoms wird angenommen, dass sich ein Elektron auf
einer Kreisbahn (strahlungslos) im Coulomb-Potential des Protons bewegt.
a) Geben Sie die kinetische und potentielle Energie des Elektrons als Funktion des Abstands r vom Proton an. Wie groß ist der Drehimpuls des Elektrons als Funktion von
r?
b) Nach dem 3. Bohr’schen Postulat soll der Drehimpuls “gequantelt” sein und nur
Werte von L = nh̄, n = 1, 2, ... annehmen dürfen. Welche Werte für die möglichen
Radien rn und die Gesamtenergie En des Elektrons ergeben sich?
c) Die exakten quantenmechanischen Lösungen für das Wasserstoffatom werden durch
die Quantenzahlen n, l und m charakterisiert. Welche Werte können diese Quantenzahlen jeweils annehmen und was ist hier der größtmögliche Wert des Drehimpulses
für einen Zustand n?
d) Diskutieren Sie kurz die Unzulänglichkeiten des Bohr‘schen Modells im Vergleich zur
korrekten quantenmechanischen Behandlung des Wasserstoffproblems. (mindestens
drei)
Aufgabe 4: Ionisationsenergie
Die Ionisationsenergie ist die Energie, die man benötigt, um ein Elektron aus einem Atom
zu entfernen. Bestimmen Sie die Ionisationsenergien von
a) einem Wasserstoffatom, dessen Elektron sich im angeregten Zustand mit n = 3 befindet.
b) He+ im n = 2-Zustand (Heliumkern, einfach ionisiert, d.h. nur ein Elektron, das sich
im n = 2-Zustand befindet)
c) Li++ im n = 4-Zustand.
Hinweis: Der He-Kern enthält 2 Protonen, der Lithium-Kern 3 Protonen.
Rydberg-Energie: E0 = 13, 6 eV
2
Aufgabe 5: Drehimpuls
~ für die Bahn eines Elektrons im
a) Berechnen Sie die Länge der Drehimpulsvektoren L
Zustand mit den Drehimpulsquantenzahlen l = 0, l = 1 und l = 2.
b) Bestimmen Sie für diese drei Fälle die möglichen z-Komponenten des Bahndrehim~ durch geeignete graphische Konstruktion.
pulsvektors L
c) Wie sehen für das Beispiel l = 1 die magnetischen Momente aus?
—————————————————————————————————————————–
Die Übungsaufgaben finden Sie auch im Internet unter der URL:
http://www-ekp.physik.uni-karlsruhe.de/~tkuhr/AKdPh
3