Bewegung von Elektronen in einem homogenen elektrischen Feld

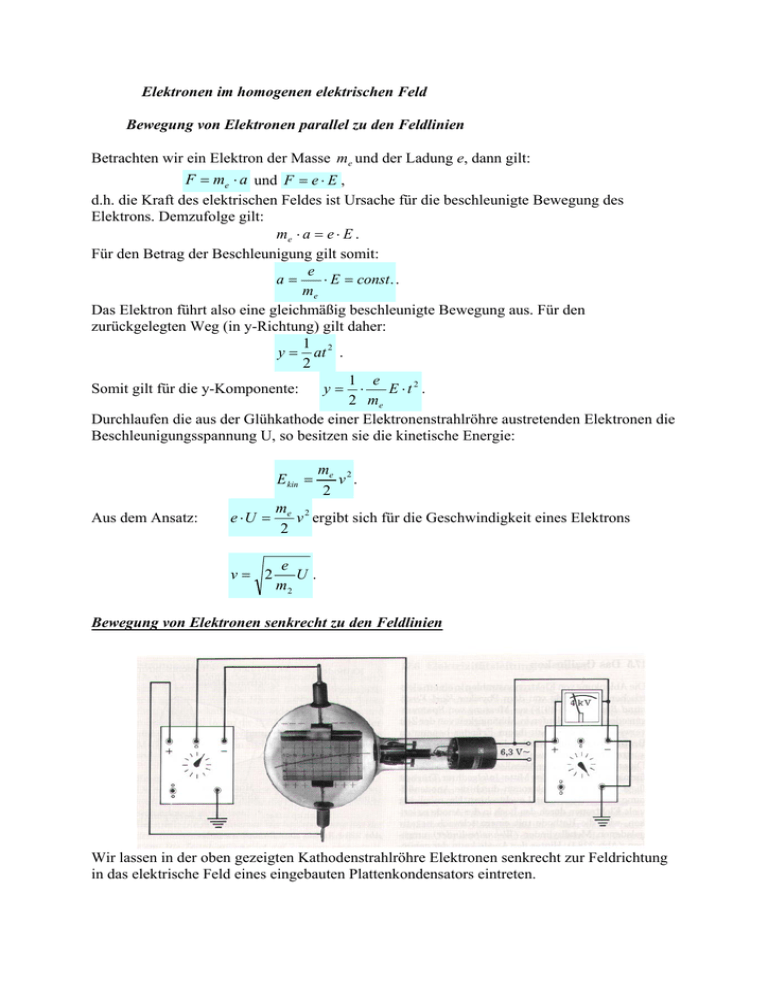
Elektronen im homogenen elektrischen Feld
Bewegung von Elektronen parallel zu den Feldlinien
Betrachten wir ein Elektron der Masse me und der Ladung e, dann gilt:
F = me ⋅ a und F = e ⋅ E ,
d.h. die Kraft des elektrischen Feldes ist Ursache für die beschleunigte Bewegung des
Elektrons. Demzufolge gilt:
me ⋅ a = e ⋅ E .
Für den Betrag der Beschleunigung gilt somit:
e
a=
⋅ E = const . .
me
Das Elektron führt also eine gleichmäßig beschleunigte Bewegung aus. Für den
zurückgelegten Weg (in y-Richtung) gilt daher:
1
y = at 2 .
2
1 e
Somit gilt für die y-Komponente:
y= ⋅
E ⋅t2 .
2 me
Durchlaufen die aus der Glühkathode einer Elektronenstrahlröhre austretenden Elektronen die
Beschleunigungsspannung U, so besitzen sie die kinetische Energie:
E kin =
Aus dem Ansatz:
me 2
v .
2
e ⋅U =
me 2
v ergibt sich für die Geschwindigkeit eines Elektrons
2
v= 2
e
U.
m2
Bewegung von Elektronen senkrecht zu den Feldlinien
Wir lassen in der oben gezeigten Kathodenstrahlröhre Elektronen senkrecht zur Feldrichtung
in das elektrische Feld eines eingebauten Plattenkondensators eintreten.
Hat das Elektron die Anfangsgeschwindigkeit v 0 , so überlagern sich gleichförmige
horizontale und gleichmäßig beschleunigte vertikale Bewegung. Dieser Vorgang lässt sich
analog mit dem waagerechten Wurf vergleichen.
In y-Richtung besitzt das Elektron die konstante Beschleunigung:
e ⋅ Ey
F
e Uy
ay =
=
=
⋅
.
me
me
me d
Die Bewegung des Elektrons in x-Richtung wird beschrieben durch:
1
1 e ⋅ Ey 2
Richtung:
⋅t .
y = ayt 2 = ⋅
2
2 me
x = v0 t und in y-
x2
⇒t = 2
v0
2
1 e ⋅ Ey x2
⇒y= ⋅
⋅
2 me v02
1 e ⋅ Ey
⇒y=
⋅ x2
2
2 me ⋅ v 0
Die Bahnkurve eines geladenen Teilchens, das senkrecht zu den Feldlinien in das elektrische
Feld eines Kondensators einfliegt, ist ein Parabelbogen.