Elektrotechnik II Wechselstromrechnung

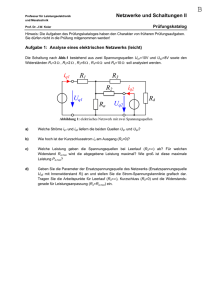
Elektrotechnik II
Professur für Leistungselektronik
und Messtechnik
Hilfestellung zur Übung Nr. 2
Prof. Dr. J. W. Kolar
Wechselstromrechnung
Aufgabe 1: Leistungsanpassung
a)
Die Quelle Iq2 liefert einen rein komplexen Strom. Dies bedeutet, dass die beiden Ströme Iq1
und Iq2 eine Phasenverschiebung von 90° aufweisen. Werden die beiden Stromquellen einzeln
betrachtet, muss diese Phasenverschiebung zur Berechnung der verfügbaren (d.h. dem
Verbraucher maximal abgebbaren) Leistung (ein Effektivwert!) nicht berücksichtigt werden.
Allgemein wird die maximal verfügbare Leistung Pmax durch den Innenwirkwiderstand Ri bzw.
durch den Innenwirkleitwert Gi der Quelle bestimmt:
Pmax =
U q2
4 ⋅ Ri
, bzw. Pmax =
I q2
4 ⋅ Gi
Zur Berechnung der Leistungen müssen die komplexen Leitwerte allerdings zuerst in die Wirkund Blindkomponenten aufgetrennt werden.
Zwischenresultate: Yi1 = Gi1 + jBi1 = 4.33mS + j2.5mS, P1 max = 519.6W
b)
Wird Leistungsanpassung verlangt, muss der Innenleitwert Yi konjugiert komplex zum
Verbraucherleitwert Ya sein. Um Ya für die gesamte Schaltung zu berechnen, müssen die beiden Quellen allerdings zunächst bezüglich der Klemmen a und b in eine Ersatzstromquelle
umgewandelt werden (IqE = Iq1 + Iq2 und YiE = Yi1 + Yi2).
Zwischenresultat: Ya = Y*iE = 9.33mS + j6.16mS
c)
Zwischenresultat: Pa max = 670W
d)
Am Verbraucher tritt bei Anpassung die Spannung Ua = IqE / 2·GiE auf. Zur Berechnung des
Klemmenstroms Ia1 (Ia2) muss berücksichtigt werden, dass ein Teil von Iq1 (Iq2) durch Yi1 (Yi2)
fliesst (Knotenregel anwenden)!
Alternativ können die Klemmenströme Ia1 und Ia2 auch mit der Stromteilerregel berechnet werden (vgl. Abb. 1). So folgt z.B. für den Strom in Yi1
I Yi1
Y i1
=
I q1 + I q 2 Y Gesamt
und daraus mit der Knotenregel der gesuchte Strom Ia1.
Zwischenresultat: Ia2 = Iq2 - Yi2·Ua= -2.66A + j4.32A
e)
Mit den nun bekannten Klemmenströmen lassen sich die Wirkleistungen berechnen, welche
die jeweiligen Quellen an die Last liefern.
Resultat: Pa1 = 171.1W
1
Elektrotechnik II
Professur für Leistungselektronik
und Messtechnik
Hilfestellung zur Übung Nr. 2
Prof. Dr. J. W. Kolar
Iq1+Iq2
Iq1
Iq2
IYi1
Ia
IYi2
Yi1
Ya
Yi2
Abb. 1: Berechnung der Klemmenströme mit der Stromteilerregel
Aufgabe 2: Blindstromkompensation
•
Die Leuchtstoffröhre wird als reiner Wirkwiderstand RL modelliert, in welchem durch den gegebenen Strom IL die bekannte Wirkleistung PL umgesetzt wird. Die gesuchte Spannung UL
kann also direkt berechnet werden.
Zwischenresultat: UL = 95.2V
•
Da die Effektivwerte von U und IL bekannt sind, kann die Scheinleistungsaufnahme SR der
Reihenschaltung von Leuchtstoffröhre und Drossel berechnet werden. Der Wirkfaktor cos φR
berechnet sich aus dem Zusammenhang zwischen der (gegebenen) Wirkleistung P der Reihenschaltung und der Scheinleistung SR.
Zwischenresultate: SR = 92.4VA, cos φR = 0.53
•
Die Kapazität C soll den Blindleistungsbedarf der Drossel decken, so dass sich die gesamte
Schaltung (also inkl. Kapazität) vom speisenden Netz her gesehen wie ein reiner Wirkwiderstand verhält, also U und I in Phase sind (vgl. Abb. 2). Die Grösse der Kapazität C lässt sich
durch Vergleich der in der Kapazität umgesetzten Blindleistung QC mit der in der Reihenschaltung von Lampe und Drossel umgesetzten Blindleistung QR bestimmen (QR + QC = 0).
(Zwischen)Resultat: QR = 78.3var, C = 5.15μF
Abb. 2: Schaltung der Leuchtstofflampe (a), welche wie ein Wirkwiderstand am Netz erscheinen soll,
und dazugehörendes (unmassstäbliches) Zeigerdiagramm (b)
2
Elektrotechnik II
Professur für Leistungselektronik
und Messtechnik
Hilfestellung zur Übung Nr. 2
Prof. Dr. J. W. Kolar
Aufgabe 3: Reihenschaltung von Wirk- und Blindwiderständen
•
Aus den 3 Strommessungen lassen sich die jeweiligen Scheinwiderstände Z, Z′ und Z″ berechnen, wobei die Messung 1 zwischen den Klemmen a und b gerade den Betrag des Blindwiderstands von C′ ergibt. Der Kapazitätswert von C′ kann nicht bestimmt werden, da die
Kreisfrequenz der Sinusspannung U nicht bekannt ist.
Zwischenresultate: Z = 5kΩ, XC′ = 2kΩ
•
Aus dem gemessenen Strom I und der dazugehörenden Wirkleistung P lässt sich der Betrag
des Wirkwiderstandes R bestimmen.
•
X ist ein Blindwiderstand (Kapazität oder Induktivität), d.h. sein Zeiger steht im Widerstandszeigerdiagramm senkrecht auf demjenigen von R, und der Satz von Pythagoras kann angewendet werden. (Der Scheinwiderstand Z ist ja durch die Messung bekannt ...)
Zwischenresultat: X = 2kΩ
•
Ob nun X eine Kapazität oder Induktivität ist, folgt aus dem Widerstandszeigerdiagramm der
gesamten Schaltung. Es können zwei verschiedene Zeigerdiagramme gezeichnet werden, eines mit der Annahme, dass X eine Kapazität ist, und das andere mit der Annahme, dass X eine Induktivität ist. Von den zwei möglichen Widerstandszeigerdiagrammen passt dann allerdings nur eines zu den berechneten Scheinwiderständen!
3