pdf-file

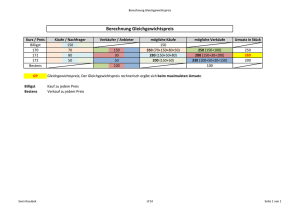
Mathematische Modellierung
Dozent: Prof. Dr. Martin Burger
Assistenz: Dipl. Math. Markus Knappitsch
2. Übungszettel. Abgabe: 25.10.2012
http://wwwmath.uni-muenster.de/num/Vorlesungen/Modellierung WS12/
Aufgabe 1:[Der geheimnisvolle Mord]
In den frühen Morgenstunden der Halloweennacht wird auf dem Vorplatz des mathematischen Institutes eine Leiche gefunden. Da der Rechtsmediziner Boerne aus Münster
immer noch krank ist, muss Kommissar Thiel den Todeszeitpunkt des Mordopfers allein bestimmen. Er erinnert sich daran, dass nach dem Newtonschen Abkühlungsgesetz
die Abkühlung eines Körpers (negative Temperaturänderung pro Zeit) proportional zur
Differenz von Körpertemperatur und Umgebungstemperatur ist. Daher misst er die Temperatur des Opfers um 6:13 Uhr, sie beträgt 22◦ C . Leider kennt Thiel die Proportionalitätskonstante nicht. Daher misst er um 6:43 die Temperatur des Opfers erneut. Sie
beträgt nun 20◦ C . Die Außentemperatur beträgt 2◦ C und kann als konstant angenommen werden. Die Körpertemperatur zum Todeszeitpunkt wird mit gesunden 37◦ C
angenommen. Helfen Sie Kommissar Thiel!
1. Zu welcher Uhrzeit wurde der Mord verübt?
2. Skalieren Sie das Modell und führen Sie eine Sensitivitätsanalyse für die Mordzeit
bezüglich der Körpertemperatur zum Mordzeitpunkt durch, um den Zeitraum, in
dem Alibis benötigt werden, genau eingrenzen zu können.
3. Wer war der Mörder?
( 2+2+0 Punkte)
Aufgabe 2:[Ein Modell zur Preisanpassung]
Ein Käufer und ein Verkäufer verhandeln über den Preis einer Ware. Zu Beginn (t = 0)
liegt der Verkaufspreis (PV (0)) über dem Angebotspreis (PK (0)) des Käufers. In jedem
Zeitschritt ∆t verringert der Verkäufer
seinen Preis um einen Bruchteil der Differenz,
nämlich um A∆t PV (t) − PK (t) , während
der Käufer sein Angebot um einen Bruchteil
anhebt, nämlich um B∆t PV (t) − PK (t) .
1. Leiten Sie für kleine Zeitschritte ∆t ein asymptotisches Modell basierend auf gewöhnlichen
Differentialgleichungen her.
2. Ermitteln Sie den Gleichgewichtspreis.
3. Verifizieren Sie die exponentielle Konvergenz gegen den Gleichgewichtspreis in der
Zeit.
(2+2+2 Punkte)
Aufgabe 3:[Räuber-Beute Dynamik]
Die Dynamik zweier Spezies die in einer Räuber-Beute Beziehung zueinander stehen lässt
sich durch das folgende System zweier gewöhnlicher Differentialgleichungen modellieren:
u̇ = a1 − b1 u − c1 v u
v̇ = a2 + b2 u − c2 v v.
Dabei ist u(t) die Population der Beutespezies und v(t) die Population der Jägerspezies.
a1 , a2 , b1 , b2 , c1 , c2 sind reelle Konstanten.
1. Interpretieren Sie die Bedeutung der Reaktionsterme bzw. der Parameter ai , bi , ci ,
i = 1, 2 .
2. Reduzieren Sie durch eine Skalierung die Anzahl der Parameter im System.
3. Berechnen Sie die Fixpunkte des Systems, und testen Sie diese auf ihre Stabilität.
4. Simulieren Sie das System numerisch durch ein Eulerverfahren. Finden Sie dazu
passende Parameterbereiche. Deuten Sie das Ergebnis. Das ganze sollte etwa so
aussehen:
5. Modifizieren Sie das System so, dass es anstelle des Räuber-Beute Szenarios die Fälle
Konkurrenz und Kooperation modelliert. Im Kooperationsfall begünstigen sich die
die Spezies gegenseitig, im Konkurrenzfall liegt eine beidseitige Hemmung vor.
(2+2+3+3+2 Punkte)