Physik Formelsammlung Abitur 2014 Bremen
Werbung
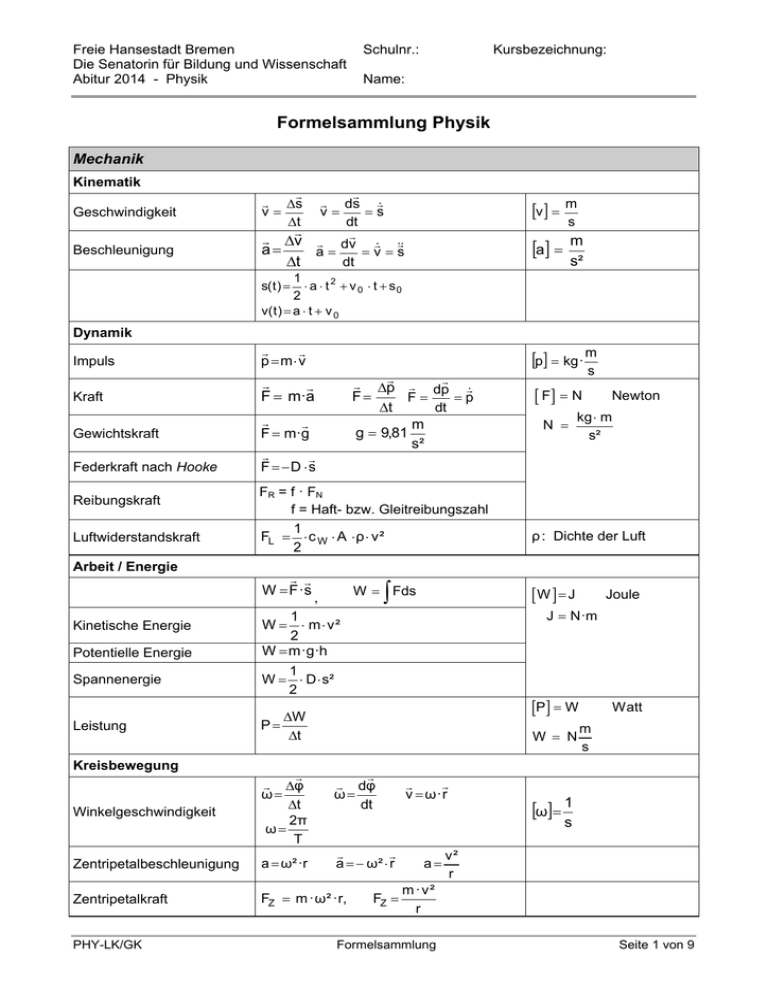
Freie Hansestadt Bremen Die Senatorin für Bildung und Wissenschaft Abitur 2014 - Physik Schulnr.: Kursbezeichnung: Name: Formelsammlung Physik Mechanik Kinematik Geschwindigkeit Beschleunigung s v t ds s v dt v dv a a vs t dt v m s m s² a 1 a t 2 v 0 t s0 2 v( t ) a t v 0 s( t ) Dynamik Impuls p m v Kraft F m·a Gewichtskraft F m·g Federkraft nach Hooke F D s Reibungskraft Luftwiderstandskraft Arbeit / Energie Kinetische Energie Potentielle Energie Spannenergie Leistung Kreisbewegung p kg · m p dp F p F t dt m g 9,81 s² FR = f · FN f = Haft- bzw. Gleitreibungszahl 1 FL c W A ρ v ² 2 W F ·s N kg m s² ρ : Dichte der Luft W N Zentripetalbeschleunigung a ω² ·r Zentripetalkraft FZ m · ω ² · r, Joule P W W P t Winkelgeschwindigkeit Newton J N·m 1 W m v² 2 W m ·g·h 1 W D s² 2 φ ω t 2π ω T PHY-LK/GK F N W J W Fds , s dφ ω dt v ω·r Watt m s ω 1 s a ω² r FZ a v² r m ·v² r Formelsammlung Seite 1 von 9 Freie Hansestadt Bremen Die Senatorin für Bildung und Wissenschaft Abitur 2014 - Physik Mechanik Gravitation Gravitationskraft 3. Keplersches Gesetz F G γ · T12 a13 m1 ·m2 r² = 6,672·10-11 T22 a1,2: a 32 Potentielle Energie Wpot FG dr γ r m1 ·m 2 r m³ kg s² große Halbachsen Bezugspunkt im Unendlichen Gesamtenergie auf Kreisbahn W ges γ m 1 ·m 2 2r Bezugspunkt im Unendlichen Gesamtenergie auf Ellipsenbahn W ges γ m1 ·m 2 2a a: große Halbachse Thermodynamik Universelle Gasgleichung p: V: T: R: Druck Volumen Temperatur in Kelvin universelle Gaskonstante J R 8,3145 mol K p V n R T Absolute Nullpunktstemperatur T0 0 273,15C ˆ 0K T0 U Q W isotherm: 1. Hauptsatz der Thermodynamik Q W mit T = const. Q U p V mit p = const. isobar: isochor: Wkin,mittel Wkin Grundgleichung der kinetischen Gastheorie pV Wirkungsgrad PHY-LK/GK Q: W: Änderung der inneren Energie Änderung der Wärmeenergie Änderung der mechanischen Energie Q U mit V = const. Mittlere kinetische Energie Wkin,mittel Wkin Entropieänderung U : 3 kT 2 2 N Wkin,mittel 3 k: Boltzmannkonstante J k 1,3806 10 23 K N: Anzahl der Teilchen im Volumen V Q T Q Q2 Q η 1 1 2 Q1 Q1 zugeführte Wärmeenergie Q1 0 abgegebene Wärmeenergie Q2 0 S Formelsammlung Seite 2 von 9 Freie Hansestadt Bremen Die Senatorin für Bildung und Wissenschaft Abitur 2014 - Physik Thermodynamik T2 T1 Idealer Wirkungsgrad η 1 Reversibler Stirlingscher Kreisprozess Q1 Q 2 0 T1 T2 Irreversibler Stirlingscher Kreisprozess Q1 Q 2 0 T1 T2 Elektrisches Feld W Q [U] = V Volt J=C·V Spannung U φ Stromstärke I Leistung P=U·I [P] = W Watt Ohmsches Gesetz U=R·I [R] = Ω Ohm Elektrische Feldstärke F E QP Flächenladungsdichte σ U Q t Q A [Q] = C = A·s Coulomb [I]=A Ampere ε 0 8,854·10 12 σ ε 0 E As Vm Radialfeld Coulomb-Kraft FC 1 Q1 Q 2 · 4πε 0 r² Kondensator Q U Kapazität (allg.) C Kapazität des Plattenkondensators C ε 0 ·εr · Feldstärke E Kondensatoraufladung t U I( t ) 0 e RC R Kondensatorentladung t U I( t ) 0 e RC R Arbeit / Energie (Kondensator) 1 W el C U² 2 [C] = F A d U d d: Abstand zwischen den Platten 1 1 t RC U C ( t ) U 0 1 e 1 PHY-LK/GK Farad UC ( t ) U0 e Formelsammlung 1 t RC Seite 3 von 9 Freie Hansestadt Bremen Die Senatorin für Bildung und Wissenschaft Abitur 2014 - Physik Magnetisches Feld [B] = T Tesla V · s T = m² Kraft auf einen stromdurchflossenen Leiter F=B·I· Lorentzkraft F=Q·v·B Magnetfeld einer Zylinderspule B μ 0 μR · Arbeit / Energie (Spule) 1 Wmag L I² 2 I·n μ0 4π ·107 Vs Am Induktion Induzierte Spannung dI dt Selbstinduktion Uind L · Hall-Spannung UH v B b A L μ 0 μ R ·n² · L H H Henry Vs A b: Breite des Hallstreifens Schwingungen Ungedämpfte, harmonische Schwingung Zeit-Weg-Gesetz s(t) = ŝ · sin(t) Zeit-GeschwindigkeitGesetz v(t) = v̂ · cos (t) v(t) = ŝ · · cos (t) Zeit-BeschleunigungGesetz a(t) = ŝ · ² · sin(t) a(t) = â · sin(t) a(t) = ² · s(t) Richtgröße D = m · ² Energie des harmonischen Oszillators W= m 2 ŝ2 1 2 Gedämpfte Schwingung Zeit-Weg-Gesetz s(t) = ŝ · e-kt · sin (t) Federpendel Schwingungsdauer T 2π · m D Fadenpendel Schwingungsdauer T 2π · g Elektrischer Schwingkreis Thomsonsche T 2π · L C Schwingungsgleichung PHY-LK/GK Formelsammlung Seite 4 von 9 Freie Hansestadt Bremen Die Senatorin für Bildung und Wissenschaft Abitur 2014 - Physik Wellen Wellengleichung t x s( x, t ) ŝ · sin 2π T λ Ausbreitungsgeschwindigkeit einer Welle c=·f Doppler-Effekt f' f c vE c vS Interferenz bei Licht am Doppelspalt bzw. am Gitter Maxima Minima Spektralfarben d · sin (n)= n · (n = 0, 1, 2, 3, ...) 2n 1 · 2 (n = 1, 2, 3, ...) d · sin (n) = rot orange gelb grün blau indigo violett 660 nm – 780 nm 595 nm – 660 nm 575 nm – 595 nm 490 nm – 575 nm 440 nm – 490 nm 420 nm – 440 nm 390 nm – 420 nm Relativitätstheorie v ·x c ² t' v² 1 c² v t' · x' c² t v² 1 c² z = z' t x v ·t x' v² 1 c² Lorentz-Transformationen x x' v · t' 1 v² c² y = y' Längenkontraktion Zeitdilatation k 1 v² c² Ungestrichen sind die Größen in dem System, in dem der Beobachter ruht. Gestrichen sind die Größen in dem dazu relativ bewegten System. Eigenlänge k kontrahierte Länge t' t 1 v² c² Minkowski-Diagramm Einheit PHY-LK/GK e' e c² v² c² v² tan v c Formelsammlung Winkel zwischen den Bezugssystemen Seite 5 von 9 Freie Hansestadt Bremen Die Senatorin für Bildung und Wissenschaft Abitur 2014 - Physik Relativitätstheorie u v u v 1 2 c Relativistische Geschwindigkeitsaddition u Relativistischer DopplerEffekt f f ' Dynamische Masse u : Geschwindigkeit eines Körpers relativ zum S System v : Geschwindigkeit des S Systems relativ zum S System u : Geschwindigkeit des Körpers im S System cv cv m0 m 1 v² c² Energie Gesamtenergie W m c2 Ruheenergie W0 m 0 c 2 Energie-ImpulsBeziehung W 2 c p W02 2 Quantenphysik Photonen Energie eines Photons h = 6,626·10-34 Js W hf Mikroobjekte De Broglie Wellenlänge λ h p Compton-Effekt Energiebilanz h f Wkin h f Wellenlängenänderung = C ( 1 – cos () ) C = 2,42 · 10-12 m Compton-Wellenlänge Bragg-Reflexion Bragg-Gleichung n λ 2d sin (), (n= 1, 2,…) Heisenbergsche Unschärferelation Heisenbergsche Unschärferelation PHY-LK/GK x p h Formelsammlung Seite 6 von 9 Freie Hansestadt Bremen Die Senatorin für Bildung und Wissenschaft Abitur 2014 - Physik Atom- und Kernphysik Energie eines in einem linearen Potentialtopf der Breite a mit unendlich hohen Wänden eingeschlossenen Teilchens Wn Absorptionsgesetz I(d) I0 e kd Zerfallsgesetz N( t ) N0 e λt h² ·n² 8 ·m ·a ² Atom- und Kernphysik A( t ) Aktivität Kernradius d N( t ) (t ) N dt [A] = Bq A ( t ) A 0 e λt r r0 3 A Becquerel 1 Bq = s r0 = 1,46 · 10-15 m A ist hier die Massezahl Konstante Größen Lichtgeschwindigkeit im Vakuum c = 2,998·108 Schallgeschwindigkeit in Luft cS = 332 m Gravitationskonstante = 6,672·10-11 Elektrische Feldkonstante m s s m³ kg s² As 1 ε 0 8,854 10 12 Vm μ0 c 2 Magnetische Feldkonstante 0= 4··10-7 Vs Elementarladung e = 1,602 · 10-19 C Ruhemasse eines Elektrons me = 9,109 · 10-31 kg Ruhemasse eines Protons mp = 1,672 · 10-27 kg Ruhemasse eines Neutrons mn = 1,675 · 10-27 kg Atomare Masseneinheit u = 1,661 · 10-27 kg Plancksches Wirkungsquantum h = 6,626 · 10-34 Js Avogadro-Konstante NA = 6,022 · 1026 Absolute Nullpunktstemperatur T0 0 273,15C ˆ 0K T0 PHY-LK/GK Am Formelsammlung 1 kmol Seite 7 von 9 Freie Hansestadt Bremen Die Senatorin für Bildung und Wissenschaft Abitur 2014 - Physik Astronomische Daten Mittlerer Erdradius rE = 6371,04 km Masse der Erde mE = 5,9736 · 1024 kg Mittlere Entfernung Erde – Sonne 1 AE = 1,496 · 1011 m SI - Vorsätze Tera T 1012 Milli m 10-3 Giga G 109 Mikro 10-6 Mega M 106 Nano n 10-9 Kilo k 103 Piko p 10-12 Mathematische Hilfsmittel Dreieck 1 A = ·g·h 2 Kreis U = 2· · r A = · r² Kugel 4 V π r3 3 O 4 π r2 Ellipsengleichung PHY-LK/GK x2 a2 y2 b2 1 Formelsammlung Seite 8 von 9 Freie Hansestadt Bremen Die Senatorin für Bildung und Wissenschaft Abitur 2014 - Physik Trigonometrische Beziehungen im rechtwinkligen Dreieck Sinus sin( ) Gegenkathete a Hypotenuse c Cosinus cos( ) Ankathete b Hypotenuse c Tangens tan( ) Gegenkathete a Ankathete b Trigonometrische Beziehungen im beliebigen ebenen Dreieck Sinussatz sin ( α) sin (β) sin ( γ ) a b c Kosinussatz a 2 b 2 c 2 2bc cos(α) Funktion f(x) Ableitungsfunktion f (x) xn n x n1 1 x Stammfunktion f(x)dx xn 1 c , (n -1) n 1 1 ln x c , (x 0) x2 e ax a ea x 1 a x e c a ln (x) 1 x x ln (x) - x c , ( x > 0 ) sin (x) cos (x) cos (x) c cos (x) -sin (x) sin (x) c tan (x) PHY-LK/GK 1 ln cos( x ) c cos 2 ( x ) Formelsammlung Seite 9 von 9