Formelsammlung Physik Zentralabitur neu - s
Werbung
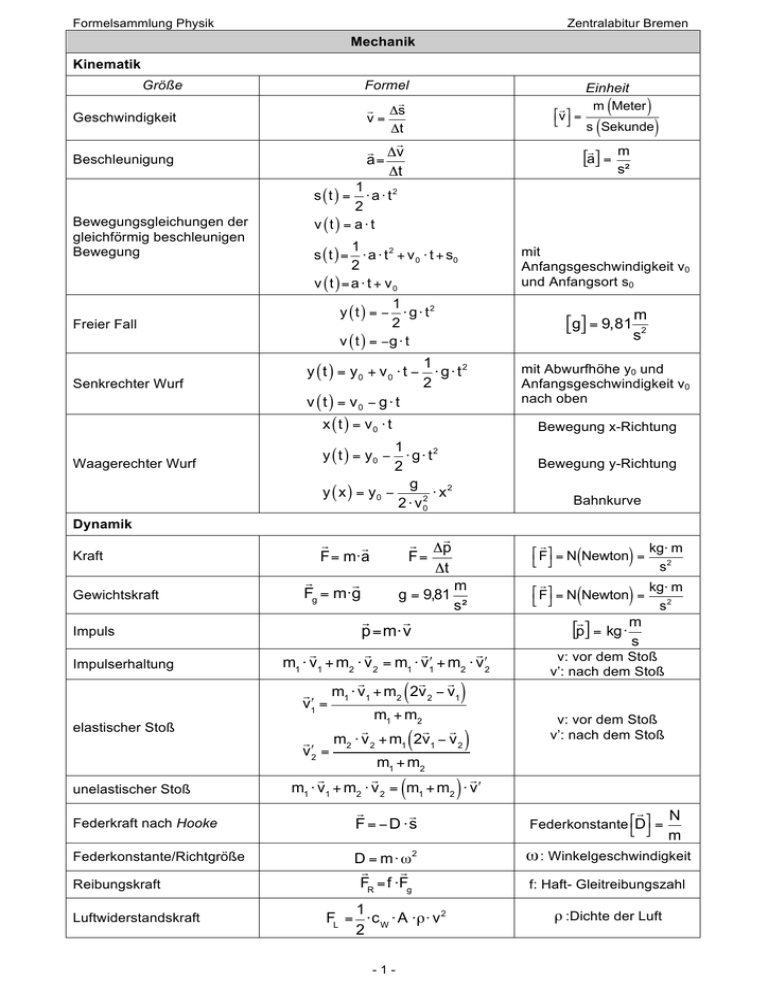
Formelsammlung Physik Zentralabitur Bremen Mechanik Kinematik Größe Formel Δs v= Δt Geschwindigkeit !v # = " $ Δv a= Δt Beschleunigung Einheit m (Meter ) ( s Sekunde [a] = ) m s² 1 ⋅ a ⋅ t2 2 v (t ) = a ⋅ t s (t ) = Bewegungsgleichungen der gleichförmig beschleunigen Bewegung Freier Fall Senkrechter Wurf 1 s ( t ) = ⋅ a ⋅ t 2 + v 0 ⋅ t + s0 2 v (t ) = a ⋅ t + v0 mit Anfangsgeschwindigkeit v0 und Anfangsort s0 1 y (t ) = − ⋅ g ⋅ t2 2 v ( t ) = −g ⋅ t [g] = 9,81 s2 y ( t ) = y0 + v 0 ⋅ t − m 1 ⋅ g ⋅ t2 2 v (t ) = v0 − g ⋅ t x ( t ) = v0 ⋅ t Waagerechter Wurf Bewegung x-Richtung 1 ⋅ g ⋅ t2 2 g y ( x ) = y0 − ⋅ x2 2 2 ⋅ v0 y ( t ) = y0 − Dynamik Kraft Gewichtskraft Impuls Impulserhaltung elastischer Stoß unelastischer Stoß Federkraft nach Hooke Federkonstante/Richtgröße Reibungskraft Luftwiderstandskraft Bewegung y-Richtung Bahnkurve Δp F= Δt F= m·a Fg = m·g g = 9,81 p = m⋅ v m s² ( F = −D ⋅s D = m ⋅ ω2 FR = f ⋅Fg 1 FL = ⋅c W ⋅ A ⋅ρ⋅ v 2 2 ! F# = N Newton = kg⋅ m " $ s2 ! F# = N Newton = kg⋅ m " $ s2 ( ) ( ) [p] = kg · m m1 ⋅ v1 + m2 ⋅ v 2 = m1 ⋅ v"1 + m2 ⋅ v"2 m1 ⋅ v1 + m2 ( 2v 2 − v1) v!1 = m1 + m2 m2 ⋅ v 2 + m1 ( 2v1 − v 2 ) v!2 = m1 + m2 m1 ⋅ v1 + m2 ⋅ v 2 = m1 + m2 ⋅ v" -1- mit Abwurfhöhe y0 und Anfangsgeschwindigkeit v0 nach oben s v: vor dem Stoß v’: nach dem Stoß v: vor dem Stoß v’: nach dem Stoß ) Federkonstante !"D#$ = N m ω : Winkelgeschwindigkeit f: Haft- Gleitreibungszahl ρ :Dichte der Luft Formelsammlung Physik Zentralabitur Bremen Arbeit / Energie Größe Formel !W # = Nm =J Joule " $ 1 Ekin = ⋅ m⋅v 2 2 !E # = 1 Nm = 1J Joule " kin $ Arbeit kinetische Energie Einheit W = F ·s ( Epot =m·g·h = Fg ⋅ h potenzielle Energie 1 ESpann = ⋅ D⋅s2 2 Spannenergie W t P= Leistung !E " pot ) ( ) # = 1 Nm = 1J (Joule) $ Federkonstante !"D#$ = [P] = W ( Watt ) = N m Nm s Kreisbewegung Winkelgeschwindigkeit / Frequenz ω= Δϕ 2π n 1 = ; f= = ; ω = 2π ⋅ f Δt T t T Bahngeschwindigkeit v = ω·r Zentripetalbeschleunigung a = ω²·r Zentripetalkraft v= 1 2π ⋅ r T [v ] = m v² r m·v² FZ = r [a] = a= FZ = m·ω²·r 1 [ω] = s ; [f ] = Hz (Hertz ) = s s m s² [FZ ] = N(Newton) Gravitation Gravitationskraft FG =G· T12 3. Keplersches Gesetz Potentielle Energie im Gravitationsfeld a13 Epot = ∞ ∫F G m1 ·m2 = r2 T22 r m1 ⋅ m2 r Bezugspunkt im Unendlichen m1 ⋅ m2 2r m ⋅m = −G 1 2 2a Gesamtenergie auf Kreisbahn Eges = −G Gesamtenergie auf Ellipsenbahn Eges m3 kg·s2 a1,2: große Halbachsen a32 dr = −G G= 6,672·10−11 Bezugspunkt im Unendlichen a: große Halbachse Thermodynamik Universelle Gasgleichung Absoluter Nullpunkt p ⋅ V = n ⋅R ⋅ T T0 = 0 K = −273,15°C ΔU = ΔQ + ΔW isotherm: 1. Hauptsatz der Thermodynamik p: Druck V: Volumen T: Temperatur R: universelle Gaskonstante J R = 8,3145 mol K isobar: isochor: ΔQ = −ΔW mit T = kons tant ΔQ = ΔU + p ⋅ ΔV mit p = kons tant ΔQ = ΔU mit V = kons tant -2- K (Kelvin) ΔU: Änderung der inneren Energie ΔQ: Änderung der Wärmeenergie ΔW: Änderung der mechanischen Energie Formelsammlung Physik Zentralabitur Bremen Thermodynamik Größe Formel 3 Ekin = k ⋅ T 2 Mittlere kinetische Energie Grundgleichung der kinetischen Gastheorie Entropieänderung Wirkungsgrad Einheit k: Bolzmannkonstante J k = 1,3806 ⋅10−23 K 2 N⋅Ekin 3 ΔQ ΔS = T Q + Q2 Q η= 1 = 1+ 2 Q1 Q1 p⋅ V = N: Anzahl der Teilchen im Volumen V zugeführte Wärmeenergie Q1>0 abgeführte Wärmeenergie Q2<0 η = 1− Idealer Wirkungsgrad T2 T1 Reversibler Stirlingscher Kreisprozess Q1 Q2 + =0 T1 T2 Irreversibler Stirlingscher Kreisprozess Q1 Q2 + <0 T1 T2 Elektrodynamik Elektrisches Feld F E= QP elektrische Feldstärke Q A ( ( σ = ε0 ⋅ E Flächenladungsdichte σ= Spannung U = Δϕ U= ΔW Q ΔQ Δt Stromstärke I= elektrische Leistung P = U⋅I elektrische Energie N Newton !E# = " $ C Coulomb Eel = U⋅I⋅ t = P ⋅ t ) ) As Vm J [U] = V ( Volt ) = C C [I] = A ( Ampere ) = s !P# = W (Watt) " $ ε 0 = 8,854·10 −12 !E # = Ws (Wattsekunde) / " el $ kWh (Kilowattstunde) 1 Ws = 1 Nm = 1 Joule Radialfeld elektrische Feldstärke Coulomb-Kraft 1 Q E= · 4πε0 r 2 FC = !E# = N " $ C 1 Q1 ⋅Q2 · 2 4πε0 r [FC ] = N(Newton) Q U [C] = F (Farad) = V Kondensator Kapazität (allg.) Kapazität des Plattenkondensators C= C = εr ⋅ ε0 ⋅ -3- C A d [C] = F (Farad) Formelsammlung Physik Zentralabitur Bremen Elektrodynamik Größe Feldstärke Kondensatoraufladung Kondensatorentladung Energie im Kondensatorfeld Formel Einheit !E# = V " $ m U d 1 − t ⎞ ⎛ UC (t) = − U0 ⎜1 − e RC ⎟ ⎜ ⎟ ⎝ ⎠ E= UC (t) = − U0 ⋅ e − 1 − t U I(t) = − 0 ⋅ e RC R 1 − t U I( t) = 0 ⋅ e RC R 1 t RC 1 Wel = ⋅ C ⋅ U² 2 [W ] = J(Joule) = C ⋅ V 2 Magnetisches Feld Kraft auf einen stromdurchflossenen Leiter Lorentzkraft Magnetfeld einer Zylinderspule Induktivität einer Zylinderspule Energie des magnetischen Feldes einer Zylinderspule F = B⋅ I ⋅ FL = Q ⋅ v ⋅ B I ·n B = µ 0 ⋅ µR · A L= µ 0 ⋅ µR ·n2 ⋅ 1 Emag = ⋅L ⋅I2 2 !B# = T Tesla = V ⋅ s " $ m2 ( ) µ 0 = 4π ·10 −7 Vs Am µr : relative Permeabilität Induktion Induzierte Spannung Selbstinduktion Hall-Spannung ΔΦ Ui = −n· Δt ΔI UI = − L· Δt mit Φ = A·B L =µ0µR ·n²· UH = v ⋅ B ⋅ b A l n: Windungszahl [L ]= H(Henry) = Vs A b: Breite Metallstreifen Schwingungen Ungedämpfte, harmonische Schwingung Zeit-Weg-Gesetz Zeit- GeschwindigkeitGesetz Zeit-Beschleunigung-Gesetz Energie des harmonischen Oszillators () ( ) v ( t ) = v̂ ⋅ cos (ω ⋅ t ) v ( t ) = ŝ ⋅ ω ⋅ cos (ω ⋅ t ) s t = ŝ ⋅ sin ω ⋅ t a t = −ŝ ⋅ ω2 ⋅ sin ω ⋅ t () ( ) a ( t ) = −â ⋅ sin (ω ⋅ t ) W= 1 ⋅ m ⋅ ω2 ⋅ ŝ2 2 Federpendel m D Schwingungsdauer T = 2π · Richtgröße D = m ⋅ ω2 Fadenpendel Schwingungsdauer T = 2π · -4- g ŝ : Amplitude ω : Winkelgeschwindigkeit v̂ : Amplitude Formelsammlung Physik Zentralabitur Bremen Schwingungen Größe Formel Einheit T = 2π ⋅ L ⋅ C L: Induktivität Spule C: Kapazität Kondensator Elektromagnetischer Schwingkreis Thomsonsche Schwingungsgleichung Gedämpfte Schwingung () ( ) s t = ŝ ⋅ e−k⋅t ⋅ sin ω ⋅ t Zeit-Weg-Gesetz k: Dämpfung Wellen ⎡ ⎛ t x ⎞⎤ s(x, t) = ŝ ·sin ⎢2π ⎜ − ⎟⎥ ⎣ ⎝ T λ ⎠⎦ Wellengleichung Ausbreitungsgeschwindigkeit einer Welle c = λ⋅f f' = f ⋅ λ : Wellenlänge "λ $ = m # % f: Frequenz c − vE c − vS Sonderfall: vE « c Doppler-Effekt v ⎞ ⎛ f ' = f ⋅ ⎜1 ± ⎟ c ⎠ ⎝ Interferenz bei Licht am Doppelspalt bzw. Gitter d ⋅ sin αn = n ⋅ λ Maxima (n = 1,2,3,...) λ d ⋅ sin α = ( 2n −1) ⋅ 2 (n = 1,2,3,...) n: Ordnung der Minima n Minima Spektralfarben d: Spaltabstand oder Gitterkonstante n: Ordnung der Minima rot orange gelb grün blau indigo violett 660 nm – 780 nm 595 nm – 660 nm 575 nm – 595 nm 490 nm – 575 nm 440 nm – 490 nm 420 nm – 440 nm 390 nm – 420 nm Relativitätstheorie x' = v ·x c ² t' = v² 1− c² v t ' + · x' c² t= v² 1− c² t − x − v ·t 1− v² c² Lorentz-Transformationen x= x' + v · t ' v² 1− c² y = y! Längenkontraktion Zeitdilatation z = z! v2 c2 lR: Länge im Ruhesystem = R ⋅ 1− t = tR ⋅ 1− v2 c2 tR: Zeit im Ruhesystem -5- Formelsammlung Physik Zentralabitur Bremen Relativitätstheorie Größe Formel m= Massenveränderlichkeit mR 1− Einheit mR: Masse im Ruhesystem v2 c2 v² c² e'=e⋅ v² 1− c² 1+ Einheit im MinkowskiDiagramm v' + v v v' +1 c² c−v f = f '⋅ c+v u= relativistische Geschwindigkeitsaddition relativistischer DopplerEffekt Energie Gesamtenergie E = m ⋅ c2 Ruheenergie E = m0 ⋅ c 2 2 E2 − c ⋅ p = E02 ( ) Energie-Impuls-Beziehung Quantenphysik Photonen E = h⋅f Energie eines Photons h = 6,626 ⋅ 10−34 Js Mikroobjekte de Broglie Wellenlänge λ= h p Compton-Effekt h ⋅ f = Ekin + h ⋅ f ʹ′ Energiebilanz Δλ = λC (1− cos ϕ) Wellenlängenänderung Compton-Wellenlänge e: λ C = 2,4263 ⋅ 10 −12 m Bragg-Reflexion Bragg-Gleichung n ⋅ λ = 2d ⋅ sin(ϑ) ; (n = 1, 2, 3, ...) Heisenbergsche Unschärferelation Heisenbergsche Unschärferelation Δx ⋅ Δp ≥ h -6- x: Ort des Teilchens p: Impuls des Teilchens Formelsammlung Physik Zentralabitur Bremen Atom- und Kernphysik Größe Energie eines Teilchens in einem linearen Potenzialtopf der Breite a Formel Absorptionsgesetz h² ·n² 8 ·m ·a² I ( d) = I0 ⋅ e−kd Zerfallsgesetz N( t ) = N0 ⋅ e−λ⋅t Aktivität Einheit mit unendlich hohen Wänden Wn = dN(t) = −N'(t) dt A t = A 0 ⋅ e−λt A(t)=− 1 [ A ] = Bq (Becquerel) = s () Kernradius A: Massenzahl r = r0 ⋅ 3 A r0 = 1,46 ⋅ 10 −15 m Astronomische Daten rE = 6.371,04 km mittlerer Erdradius mittlere Entfernung Erde – Sonne 1AE = 1,496 ⋅ 1011 m Masse der Erde mE = 5,9736 ⋅ 10 24 kg Masse der Sonne mS = 1,9889 ⋅1030 kg Masse des Mondes mM = 7,349 ⋅1022 kg Konstante Größen der Physik c = 2,998 ⋅ 108 Lichtgeschwindigkeit im Vakuum c s = 332 Schallgeschwindigkeit in Luft m s G = 6,672 ⋅10−11 Gravitationskonstante ε0 = elektrische Feldkonstante magnetische Feldkonstante m s m3 kg⋅ s2 1 As = 8,854 ⋅ 10 −12 2 µ0 ⋅ c Vm Vs µ0 = 4π ⋅ 10−7 Am Ruhemasse eines Elektrons e = 1,602 ⋅ 10−19 C me = 9,109 ⋅ 10 −31 kg Ruhemasse eines Protons mp = 1,672 ⋅ 10−27 kg Ruhemasse eines Neutrons mn = 1,675 ⋅ 10 −27 kg Elementarladung u = 1,661⋅ 10−27 kg h = 6,626 ⋅ 10−34 Js 1 NA = 6,022 ⋅ 1026 kmol J k = 1,3806 ⋅10−23 K −12 λ C = 2,4263 ⋅ 10 m atomare Masseneinheit Planck’sches Wirkungsquantum Avogadro-Konstante Bolzmannkonstante Compton-Wellenlänge -7- Formelsammlung Physik Zentralabitur Bremen Mathematische Hilfsmittel Figur Umfang Fläche 1 ⋅ g⋅h 2 A = π ⋅ r2 A= U= a+b+c Dreieck Kreis U = 2π ⋅ r Kugel ----- Volumen --------- V= O = 4π ⋅ r 2 4 ⋅ π ⋅ r3 3 x 2 y2 + =1 a2 b2 Ellipsengleichung Trigonometrische Beziehungen im rechtwinkligen Dreieck Gegenkathete Hypotenuse Ankathete cos α = Hypotenuse Gegenkathete tan α = Ankathete a c b cos α = c a tan α = b sin α = Sinus Cosinus Tangens sin α = Trigonometrische Beziehungen im beliebigen Dreieck sinα sinβ sinγ = = a b c 2 2 2 2 2 2 a = b + c − 2bc ⋅ cos α b = a + c − 2ac ⋅ cos β Sinussatz Cosinussatz Funktion f(x) x Ableitungsfunktion f ’(x) n n⋅ x 1 x − Stammfunktion 1 x2 a ⋅ ea⋅x ln(x) 1 x cos(x) −sin(x) ∫ f(x) dx x n+1 + c , (n ≠ −1) n +1 n−1 ea⋅x sin(x) cos(x) c 2 = a2 + b2 − 2ab ⋅ cos γ ln x + c ; (x ≠ 0) 1 a⋅x ⋅e +c a x ⋅ ln (x) − x + c ; (x > 0) −cos(x) + c sin(x) + c SI - Vorsätze Tera T 1012 Milli m 10-3 Giga G 109 Mikro µ 10-6 Mega M 106 Nano n 10-9 Kilo k 103 Piko p 10-12 -8-











