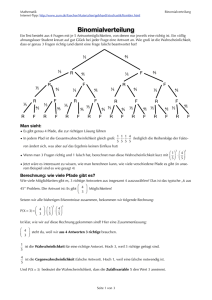
P(X ≤ 59) = 1
Werbung

Alle Bundesländer | Abitur D e i n Le r nve r z e i c h n i s Basiswissen | Aufgaben und Lösungen ◮ Stochastik | Binomialverteilung | Mit Tabelle Lösungsblatt (ausführlich) 1. In einer Tabelle für die aufsummierte Binomialverteilung, kann man die Wahrscheinlichkeit P( X ≤ 1 k ) ablesen. Ablesen aus der Tabelle für n = 20 und p = führt zu: 3 a) P( X ≤ 10) = 0, 9624 = b 96, 24% b) P( X > 10) = 1 − P( X ≤ 10) = 1 − 0, 9624 = 0, 0376 = b 3, 76% c) P(3 ≤ X ≤ 12) = P( X ≤ 12) − P( X ≤ 2) = 0, 9963 − 0, 0176 = 0, 9787 = b 97, 87% d) P(6 ≤ X ≤ 10) = P( X ≤ 10) − P( X ≤ 5) = 0, 9624 − 0, 2972 = 0, 6652 = b 66, 52% e) P( X < 8) = P( X ≤ 7) = 0, 6615 = b 66, 15% f) P( X ≥ 3) = 1 − P( X ≤ 2) = 1 − 0, 0176 = 0, 9824 = b 98, 24% 2. In einer Tabelle für die aufsummierte Binomialverteilung, kann man die Wahrscheinlichkeit P( X ≤ k ) ablesen. Es gilt n = 100 und p = 0, 4. a) P( X ≤ 30) = 0, 0248 = b 2, 48% b) P( X = 30) = P( X ≤ 30) − P( X ≤ 29) = 0, 0248 − 0, 0148 = 0, 01 = b 1% c) P( X < 40) = P( X ≤ 39) = 0, 4621 = b 46, 21% d) P( X ≥ 60) = 1 − P( X ≤ 59) = 1 − 1 ≈ 0 = b 0% e) P( X > 45) = 1 − P( X ≤ 45) = 1 − 0, 8689 = 0, 1311 = b 13, 11% f) P(22 ≤ X ≤ 54) = P( X ≤ 54) − P( X ≤ 21) = 0, 9983 − 0 = 0, 9983 = b 99, 83% 3. a) B50;0,2 (5 ≤ Z ≤ 7) = B50;0,2 ( X ≤ 7) − B50;0,2 ( X ≤ 4) = 0, 1904 − 0, 0185 = 0, 1719 = b 17, 19% b) B50;0,2 (3 ≤ Z ) = B50;0,2 ( X ≥ 3) = 1 − B50;0,2 ( X ≤ 2) = 1 − 0, 0013 = 0, 9987 = b 99, 87% c) B50;0,2 ( Z > 6) = 1 − B50;0,2 ( X ≤ 6) = 1 − 0, 1034 ≈ 0, 8966 = b 89, 66% 4. Beim Wurf einer Münze gibt es zwei mögliche Ergebnisse: Wappen“ oder Zahl“. Beide Ergebnisse ” ” treten mit der gleichen Wahrscheinlichkeit auf, nämlich jeweils mit p = 21 . In einer Tabelle für die aufsummierte Binomialverteilung, kann man die Wahrscheinlichkeit P( X ≤ k ) ablesen. Es gilt n = 50 und p = 12 . a) Höchstens 15 Mal“ bedeutet 15 Mal und weniger. Sei X die Anzahl der geworfenen Wappen“: ” ” P( A) = P( X ≤ 15) = 0, 0033 = b 0, 33% b) P( B) = P( X > 15) = 1 − P( X ≤ 15) = 1 − P( A) = 1 − P( X ≤ 15) = 1 − 0, 0033 = 0, 9967 = b 99, 67% c) P(C ) = P( X = 25) = P( X ≤ 25) − P( X ≤ 24) = 0, 5561 − 0, 4439 = 0, 1122 = b 11, 22% d) P( D ) = P(17 ≤ X ≤ 35) = P( X ≤ 35) − P( X ≤ 16) = 0, 9987 − 0, 0077 = 0, 991 = b 99, 1% e) P( E) = P(15 < X < 27) = P(16 ≤ X ≤ 26) = P( X ≤ 26) − P( X ≤ 15) = 0, 6641 − 0, 0033 = 0, 6608 = b 66, 08% c Karlsruhe 2013 | SchulLV | Patrick Huber Seite 1/6 Vervielfältigung nur innerhalb einer Lehrer-/Klassen- oder Schullizenz und mit Hinweis auf MatheLV erlaubt. www.MatheLV.net Alle Bundesländer | Abitur D e i n Le r nve r z e i c h n i s Basiswissen | Aufgaben und Lösungen ◮ Stochastik | Binomialverteilung | Mit Tabelle Lösungsblatt (ausführlich) 5. Die fünf Sektoren sind gleich groß. Damit wird jeder Sektor mit der gleichen Wahrscheinlichkeit von p = 51 = 0, 2 gedreht. In einer Tabelle für die aufsummierte Binomialverteilung kannst du die Wahrscheinlichkeit P( X ≤ k ) ablesen. Es gilt n = 50 und p = 0, 2. a) P( A) = P( X ≤ 15) = 0, 9692 = b 96, 92% b) P( B) = P(20 ≤ X ≤ 35) = P( X ≤ 35) − P( X ≤ 19) = 1 − 0, 9991 = 0, 0009 = b 0, 09% c) Die Sektoren sind von 1 bis 5 durchnummeriert. Mögliche Sektoren sind also die mit den Nummern 1, 3 und 5. Bei einem solchen Zufallsversuch, bei dem sich das Ergebnis aus mehreren Möglichkeiten zusammensetzt, berechnest du die Wahrscheinlichkeit mit der Summenregel. Da jeder der drei Sektoren mit einer Wahrscheinlichkeit von p = 0, 2 gedreht wird, ergibt sich für das Ereignis Ein Sektor mit ungerader Zahl wird gedreht“ eine Wahrscheinlichkeit von ” p∗ = 0, 2 + 0, 2 + 0, 2 = 0, 6. B50;0,6 (C ) = P(C ) = P( X ≤ 23) = 0, 0314 = b 3, 14% 6. Die Zufallsgröße X beschreibe die Anzahl der erkrankten Personen (in der Stichprobe n = 100). Wir gehen davon aus, dass die Zufallsgröße X binomialverteilt ist mit n = 100 und p = 0, 1. Die Wahrscheinlichkeit, dass unter 100 Personen genau 12 Erkrankte sind beträgt somit: P( X = 12) = P( X ≤ 12) − P( X ≤ 11) = 0, 8018 − 0, 7030 = 0, 0988 = 9, 88% Die Wahrscheinlichkeit, dass sich unter den 100 mindestens fünf Kranke befinden, ist P( X ≥ 5) = 1 − P( X ≤ 4) = 1 − 0, 0237 = 0, 9763 = 97, 63% 7. Die Zufallsgröße Z beschreibe die Anzahl der Befragten, welche die Werbeanzeige gut finden. Da von der Hypothese 20% der Befragten finden die Werbe-Anzeige gut“ ausgegangen wird, ist Z ” binomialverteilt mit n = 200 und p = 0, 20. Berechnet werden soll nun die Mindestanzahl k der Befragten, welche die Werbe-Anzeige gut finen, sodass die Hypothese H : p = 20% mit einer Wahrscheinlichkeit von mindestens 50% eingehalten wird. P( Z ≥ k ) ≥ 0, 5 1 − P( Z < k ) ≥ 0, 5 − P( Z < k) ≥ −0, 5 P( Z < k ) ≤ 0, 5 | −1 | ·(−1) | P ( Z < k ) = P ( Z ≤ k − 1) P( Z ≤ k − 1) ≤ 0, 5 Schaut man in einer geeigneten Tabelle nach, so ist P( Z ≤ 39) = B200;0,2 (39) = 0, 4718 und P( Z ≤ 40) = 0, 5422. Also ist P( Z ≤ k − 1) = P(39) ≤ 0, 5 und damit k − 1 = 39 ⇐⇒ k = 40. Es müssen mindestens 40 der Befragten die Werbeanzeige gelungen finden, so dass mit einer Wahrscheinlichkeit von mindestens 50% die Marktanalyse von 20% korrekt ist. 8. Die Zufallsgröße X beschreibe die Anzahl der fehlerhaften Chips (in der Stichprobe). Die Zufallsgröße X ist binomialverteilt mit n = 50 und p = 0, 05. 10 Chips funktionieren nicht: P( X = 10) = B50;0,05 ( X = 10) ≈ 0 c Karlsruhe 2013 | SchulLV | Patrick Huber Seite 2/6 Vervielfältigung nur innerhalb einer Lehrer-/Klassen- oder Schullizenz und mit Hinweis auf MatheLV erlaubt. www.MatheLV.net Alle Bundesländer | Abitur D e i n Le r nve r z e i c h n i s Basiswissen | Aufgaben und Lösungen ◮ Stochastik | Binomialverteilung | Mit Tabelle Lösungsblatt (ausführlich) Mehr als drei Chips sind fehlerhaft: P( X > 3) = 1 − P( X ≤ 3) = 1 − 0, 7604 = 0, 2396 = b 23, 96% Berechnen des Mindestumfangs n der Stichprobe (Mindestlänge einer Bernoulli-Kette): Die Zufallsgröße Xn steht für die Anzahl der fehlerhaften Chips in einer Stichprobe mit dem Umfang n. Die Zufallsgröße Xn ist binomialverteilt mit n unbekannt und p = 0, 05. Wir suchen also ein n mit P( Xn ≥ 1) ≥ 0, 95. P( Xn ≥ 1) ≥ 0, 95 1 − P( Xn = 0) ≥ 0, 95 − P( Xn = 0) ≥ −0, 05 P( Xn = 0) ≤ 0, 05 (n0 ) · (0, 05)0 · (0, 95)n ≤ 0, 05 (0, 95)n ≤ 0, 05 n · ln(0, 95) ≤ ln(0, 05) n≥ P ( Xn ≥ 1) = 1 − P ( Xn = 0) | −1 | ·(−1) | n unbekannt, p = 0, 05 (n0 ) = 1; (0, 05)0 = 1 | ln( ) |: ln(0, 95) Achtung: ln(0, 95) < 0! ln(0, 05) ln(0, 95) n ≥ 58, 4 Die Stichprobe muss mindestens 59 Chips umfassen. 9. a) X sei die Zufallsvariable, die angibt wie viele Mitglieder zur Generalversammlung kommen. Man geht davon aus, dass X binomialverteilt ist mit n = 100 und p = 0, 7. P( X > 80) = 1 − P( X ≤ 80) P( X > 80) = 1 − 0, 9911 siehe Tafelwerk (kumulative Tabelle) oder GTR/CAS P( X > 80) = 0, 0089 Mit einer Wahrscheinlichkeit von 0, 0089 ≈ 0, 89% kommen also mehr als 80 Mitglieder zur Generalversammlung. b) X sei die Zufallsvariable, die die Anzahl der Generalversammlungen beschreibt, an denen mehr als 80% der Mitglieder anwesend sind. Man geht davon aus, dass X binomialverteilt ist. Die Anzahl n ist dabei unbekannt und soll berechnet werden. Die Wahrscheinlichkeit p, dass eine Generalversammlung von mehr als 80 Mitgliedern besucht wird, hast du im Aufgabenteil a) berechnet: p = 0, 0089. Dann gilt c Karlsruhe 2013 | SchulLV | Patrick Huber Seite 3/6 Vervielfältigung nur innerhalb einer Lehrer-/Klassen- oder Schullizenz und mit Hinweis auf MatheLV erlaubt. www.MatheLV.net Alle Bundesländer | Abitur D e i n Le r nve r z e i c h n i s Basiswissen | Aufgaben und Lösungen ◮ Stochastik | Binomialverteilung | Mit Tabelle Lösungsblatt (ausführlich) P( X ≥ 1) > 0, 95 1 − P( X = 0) > 0, 95 | −1 − P( X = 0) > −0, 05 | ·(−1) P( X = 0) < 0, 05 | n unbekannt, p = 0, 0089 (n0 ) · (0, 0089)0 · (1 − 0, 0089)n < 0, 05 | (n0 ) = 1; (0, 0089)0 = 1 (0, 9911)n < 0, 05 | ln( ) n · ln (0, 9911) < ln(0, 05) n> |: ln(0, 9911) Achtung: ln(0, 9911) < 0! ln(0, 05) ≈ 335, 1 ln(0, 9911) Es müssen mindestens 336 Generalversammlungen abgehalten werden, damit eine Namensänderung mit einer Wahrscheinlichkeit von mindestens 95% vollzogen werden kann. 10. a) Sei X die Zufallsvariable, die die Anzahl s der stornierten Buchungen angibt. Dann ist X binomialverteilt mit n = 200 und p = 0, 05. 200 · (0, 05)s · 0, 95200−s . Es ergibt sich P(s) = P( X = s) = s Schaut man sich die Tabelle der Binomialverteilung für n = 200 und p = 0, 05 an, so kann man folgendes ablesen: P( X = 9) ≈ 0, 1277 P( X = 10) ≈ 0, 1284 P( X = 11) ≈ 0, 1167 Somit haben wir durch Probieren, dass Maximum s = 10 gefunden. Die Wahrscheinlichkeit ist für genau 10 stornierte Buchungen am größten. b) Da der Reiseanbieter nur 190 Reisen zur Verfügung hat, müssen mindestens 10 Personen ihre Reise stornieren. Sind es nur 9 oder weniger, hat der Reiseanbieter eine Doppelbuchung. X sei die Zufallsvariable, die die Anzahl der stornierten Reisen beschreibt. X sei binomialverteilt mit n = 200 und p = 0, 05. P( X ≤ 9) ≈ 0, 4547 = 45, 47% siehe Tabelle für aufsummierte Binomialverteilung c) Die 195 Personen setzen sich zusammen aus 175 Nicht-Fußballern“ und 20 Fußballern“. 5 die” ” ser 195 Personen müssen mit einem anderen Reiseanbieter reisen. Es soll die Wahrscheinlichkeit dafür bestimmt werden, dass genau 2 dieser fünf Personen Fußballer sind. 195 Es gibt insgesamt mögliche Zusammenstellungen von 5-er Gruppen. Günstig sind aber 5 nur die, bei denen und zwei Fußballer ausgewählt werden. Für diese Kom drei Nicht-Fußballer 175 20 bination gibt es · Möglichkeiten. 3 2 Für die gesuchte Wahrscheinlichkeit p gilt damit: 175 20 · 166.815.250 3 2 p= ≈ 0,0748 = 195 2.231.243.664 5 c Karlsruhe 2013 | SchulLV | Patrick Huber Seite 4/6 Vervielfältigung nur innerhalb einer Lehrer-/Klassen- oder Schullizenz und mit Hinweis auf MatheLV erlaubt. www.MatheLV.net Alle Bundesländer | Abitur D e i n Le r nve r z e i c h n i s Basiswissen | Aufgaben und Lösungen ◮ Stochastik | Binomialverteilung | Mit Tabelle Lösungsblatt (ausführlich) Mit einer Wahrscheinlichkeit von etwa 7,5 % reisen genau zwei Fußballer mit einem anderen Reiseanbieter. 11. Sei X die Zufallsgröße, die die Anzahl der verkauften Autos beschreibt. Wir gehen von einer binomialverteilung von X aus mit n = 50 und p = 0, 80. a) Erwartungswert: E( X ) = n · p = 50 · 0, 80 = 40 Erwartungsgemäß verkauft er 40 der 50 Autos. b) Sei A das Ereignis: mindestens 40, aber weniger als 45 verkaufte Autos.’” ” Zu berechnen ist: P(40 ≤ Z ≤ 44) = B50;0,80 ( Z ≤ 44) − B50;0,80 ( Z ≤ 39) ≈ 0, 952 − 0, 4164 = 0, 5356 ≈ 53, 6%. (siehe Tabellenwerte) Die Wahrscheinlichkeit dafür, dass mindestens 40 aber weniger als 45 Autos verkauft wurden, beträgt 53, 6%. c) Gesucht ist die Anzahl k der Autos, die mit einer Wahrscheinlichkeit von mehr als 97 % mindestens verkauft werden. Sei X die Anzahl der verkauften Autos. X kann wie oben als binomialverteilt angenommen werden mit n = 50 und p = 0,80. In Formeln lautet die Bedingung für unser k: P( X ≥ k ) > 0,97. Daraus folgt: P( X ≥ k ) > 0,97 1 − P( X ≤ k − 1) > 0,97 − P( X ≤ k − 1) > −0,03 P( X ≤ k − 1) < 0,03 Betrachte nun die Tabelle zur kumulierten Binomialverteilung für n = 50 und p = 0,80. Du findest den Wert für k durch systematisches Probieren: P( X ≤ 34) = 1 − 0,9692 = 0,0308: zu groß P( X ≤ 33) = 1 − 0,9856 = 0,0144: okay Damit ist k − 1 = 33, also k = 34. Mit einer Wahrscheinlichkeit von mehr als 97 % werden mindestens 34 Autos verkauft. 12. a) Wenn keine Qualitätsverbesserung eingetreten ist, beträgt die Wahrscheinlichkeit für einen nicht der Norm entsprechenden Pommes p = 10%. Da die satte Prämie nur dann ausbezahlt wird, wenn 18 oder weniger Pommes unter den 200 Pommes der Stichprobe sind, muss Folgendes gelten: X sei die Zufallsvariable, die die Anzahl der nicht der Norm entsprechenden Pommes beschreibt. X ist dann B200;0,1 (binomial)-verteilt. P( X ≤ 18) ≈ 0, 372 = 37, 2% Damit beträgt die Wahrscheinlichkeit, dass zufällig weniger als 18 Pommes aussortiert werden müssen 37, 2%. Mit dieser Wahrscheinlichkeit würde das Expertenteam eine Prämie erhalten, ohne eine Qualitätsverbesserung bewirkt zu haben. c Karlsruhe 2013 | SchulLV | Patrick Huber Seite 5/6 Vervielfältigung nur innerhalb einer Lehrer-/Klassen- oder Schullizenz und mit Hinweis auf MatheLV erlaubt. www.MatheLV.net Alle Bundesländer | Abitur D e i n Le r nve r z e i c h n i s Basiswissen | Aufgaben und Lösungen ◮ Stochastik | Binomialverteilung | Mit Tabelle Lösungsblatt (ausführlich) b) Ist die Wahrscheinlichkeit auf 7% gesunken, so ergibt sich eine neue (binomial)-Verteilung. Sei X wie in a), dann ist X B200;0,07 (binomial)-verteilt. Da die für die Prämie immer noch die Voraussetzung von 18 oder weniger fehlerhaften Pommes gilt, erhält man P( X > 18) = 1 − P( X ≤ 18) ≈ 1 − 0, 891 = 0, 109 = 10, 9% Somit besteht eine Wahrscheinlichkeit von 10, 9%, dass unter den 200 Pommes mehr als 18 Stück sind, die aussortiert werden müssen, obwohl der Ausschuss durch die Qualitätsverbesserung unter 7% gesenkt wurde. 13. Sei X die Zufallsvariable, die die Anzahl der Personen in der Stichprobe von n = 200 beschreibt, die das Angebot des IT-Fachmarktes kennen. Dann ist X B200;0,95 -(binomial)verteilt. Wenn die Wahrscheinlichkeit mehr als 80% betragen soll, muss man ein k finden, so dass gilt: P( X ≥ k ) > 0, 8 Schaut man sich nun die Tabelle der aufsummierten Binomialverteilung (kumulative Verteilungsfunktion) an, so findet man nur die Wahrscheinlichkeiten unterhalb von 0, 5, also X ≤ a. Wir brauchen also das Gegenereignis: 1 − P( X < k ) > 0, 8 − P( X < k) > −0, 2 P( X < k ) < 0, 2 | −1 | ·(−1) (Das > dreht sich nun um) | nun geht man nun ein Wert weiter links von k, also k − 1 P( X ≤ k − 1) < 0, 2 Den Wert für k − 1 kann man nun aus der Tabelle für die kumulative Verteilungsfunktion ablesen. k − 1 = 186 : P( X ≤ 186) ≈ 0, 1299 < 0, 2 k − 1 = 185 : P( X ≤ 187) ≈ 0, 2035 > 0, 2 k ist also zu groß Die Lösung mit k − 1 = 186 ist somit diejenige, welche die Bedingung erfüllt. Für das gesuchte k gilt also k = 186 + 1 = 187. Also mindestens 187 Befragte sollten die Werbung kennen. c Karlsruhe 2013 | SchulLV | Patrick Huber Seite 6/6 Vervielfältigung nur innerhalb einer Lehrer-/Klassen- oder Schullizenz und mit Hinweis auf MatheLV erlaubt. www.MatheLV.net