Kodierung, Zahlensysteme
Werbung
Kodierung, Zahlensysteme
Konvertierung einer ganzen Zahl z in ein System der Basis B
1. Stellenwertsysteme und Kodierung
Algorithmus:
Division von z durch B,
Ergebnis und Rest aufschreiben
Division des Ergebnisses durch B
Ergebnis und Rest aufschreiben
...
Reste in umgekehrter Reichenfolge aufschreiben
Endergebnis
Basis B des Zahlensystems, B > 1, natürliche Zahl
Ziffernmenge M = { 0, 1, 2, ... , B-1 }
reelle Zahl:
z = Σi=-
n
zi * Bi
zi C M
Beispiel:
123,456 = 1 * 102 + 2 * 101 + 3 * 100 + 4 * 10-1 + 5 * 10-2 + 6 * 10-3
wichtige Systeme: B = 2
B=8
B = 10
B = 16
Dualsystem
Oktalsystem
Dezimalsystem
Hexadezimalsystem
systematische Darstellung der Zahlen im Dualsystem
dual
dezimale Entsprechung
0
L
0
1
L0
LL
2
3
L00
L0L
4
5
LL0
LLL
6
7
L000
L00L
8
9
Bemerkung:
Anhängen einer „0“ bewirkt Verdopplung
systematische Darstellung der Zahlen im Hexadezimalsystem
hexadezimal
dezimal
0
1 ...
9
A
B C D E
F
0 1 ... 15
10 11 ...
19 1A 1B ...
1F
16 ... 31
20 21 ...
2F
32 ... 47
...
F0 F1 ...
F9 FA FB ...
FF
240 ... 255
100 101 ... 109 10A 10B
10F
256 ... 271
110 111 ...
11F
272 ... 287
...
FF0 FF1 ...
FFF
65520 ... 65535
1000 ...
65536 ...
Konvertierung echter Brüche
echter Bruch z,
Darstellung in
irgendeinem
Zahlensystem
22
11
5
2
1
:
:
:
:
:
2
2
2
2
2
=
=
=
=
=
11
5
2
1
0
Rest 0
Rest 1
Rest 1
Rest 0
Rest 1
Ergebnis:
zi C M
Ziffern im Zahlensystem
mit Basis B
Algorithmus:
Multiplikation von z mit B,
führende Ziffer aufschreiben
Multiplikation des Restbruches mit B
führende Ziffer aufschreiben
...
führende Ziffern in Reichenfolge aufschreiben
Endergebnis
Beispiel:
Konvertierung von 0,45 aus Dezimal- in Dual-System
0,45 * 2
=
0,9
z-1 = 0
0,9 * 2
=
1,8
z-2 = L
0,8 * 2
=
1,6
z-3 = L
0,6 * 2
=
1,2
z-4 = L
0,2 * 2
=
0,4
z-5 = 0
0,4 * 2
=
0,8
z-6 = 0
0,8 * 2
=
1,6
z-7 = L
...
Ergebnis: 0,45 = 0,0LLL00
Konvertierung reeller Zahlen
getrennte Konvertierung des ganzen und des gebrochenen
Anteils
L0LL0
Überprüfung: 22 = (((( 1) *2 + 0) *2 + 1) *2 +1) *2 + 0
Beispiel:
Konvertierung von 2001 aus Dezimal- in Hexadezimal-System
2001
125
7
:
:
:
16
16
16
=
=
=
125 Rest 1
7 Rest D
0 Rest 7
Ergebnis:
7D1
Überprüfung: 2001 = (( 7) *16) + 13) *16 + 1
Konvertierung von 1998: Ergebnis:
7CE
Umkehrung des Verfahrens (Umwandlung in Dezimalsystem)
funktioniert ebenso
Umwandlung: Hexadezimal
0<z<1
z = 0 , z-1 z-2 z-3 ...;
Beispiel:
Konvertierung von 22 aus Dezimal- in Dual-System
Dual
Dualdarstellung von 7D1
7
D
1
= LLL LL0L 000L
Hexadezimaldarstellung von L0LL0
L 0LL0
= 1
6
(6 entspricht 0LL0,
führende Nullen werden weggelassen)
Brüche:
0,45 = 0,0LLL00LL00LL....
= 0,73
hexadezimal
Beispiele:
67,75
= L0000LL,LL
13,9375 = LL0L,LLLL
3,3
= LL,0L 00LL
23,0625
171,5
105,125
30,4375
= 17,1
= AB,8
= 69,2
= 1E,7
2. Rechnen im Dual- und im Hexadezimalsystem
Rechenregeln wie im Dezimalsystem
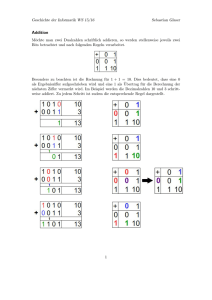
Grundaufgaben im Dualsystem (Beispiele):
Addition:
LL0LLLL0
LLL0LL
+
+
+
L L L L L L L
LL0LL0
LLL0
LLL
Grundaufgaben im Hexadezimalsystem:
Zahlenkreis für hexadezimales Addieren und Subtrahieren
F 0 1
E
2
D
3
C
4
L L L L0 L
L000LL00L
L00L0LL
B
5
A
L+0+0
=
L
L+L+L
= LL
L + L + L + L = L0 0
L+0+
L0 = L L
L+
L = L0
L+
L = L0
+
L =
L
spaltenweise
Addition
vorheriger Übertrag
neuer Übertrag
Ergebnisziffer
9 8 7
Addition:
+
4AC16
3ADEF
D9C,1 3 1
Subtraktion:
-
15BB8
ABBA
L L
E4 E4 1
1A 1A1
-
AFFE
LL00LL
Multiplikation:
ABC,903
2 DF,82E
+
85A05
Subtraktion:
LL0L00L
LL0LL0
L L
6
CACA0
L0L,L*L,0L
L0L L
L 0 LL
LL0,L LL
Division:
-
LL0LL,L:L0L = L0L,L
L0L
LLL
- L0L
L0L
- L0L
0
Subtraktion durch Addition des Komplements des Subtrahenden
Rückführung der Subtraktion auf Addition
(Multiplikation auf Addition / Division auf Subtraktion
alle arithmetischen Operationen auf Addition)
Definition:
c = b – a heißt Komplement von a bezüglich b
(mit a,b C N, b > a >=0)
Beispiel:
Komplement von 64 bezüglich 10000:
9936
Algorithmus zur Komplementbildung:
- benutze für jede Spalte der Bezugszahl die größte
Ziffer einer vorgegebenen Basis B
- bestimme in jeder Spalte die Ergänzung der Ziffern
einer vorgegebenen Zahl zu der jeweiligen
Bezugsziffer
- Addiere eine „1“
Beispiel:
0064:
9999
0064
9935
Komplement = 9936
+1
Subtraktion im Dezimal- und Dualsystem durch Komplement-Addition:
herkömmliche Subtraktion
320
64
256
-
L0LL0
L0L0
Komplement-Addition
320
+ 9936
10256
„1“ wird weggelassen
L0LL0
+ LLL0LL0
LL00
L000LL00
Komplementbildung im Dualsystem besonders einfach:
Ziffernweise 0
L, L
0, + „L“ (Korrektur-„1“)
3. Speicherung ganzer Zahlen im Festkommawort von 2
Bytes (PASCAL)
Beispiel: Darstellung von 22 = L 0 L L 0
7
6
5
4
3
2
1
0
15
14
13
12
11
10
9
8
0
0
0
L
0
L
L
0
0
0
0
0
0
0
0
0
höherwertiges Byte rechts, niederwertiges Byte links
Bit 15 enthält Vorzeichen, andere enthalten die Stellenwerte
„0“ bedeutet „+“
„L“ bedeutet „-“
Darstellung von –22 :
L L L 0 L 0
L
0
L
L
L
L
L
L
L
Probe: 22 22 =
0
Addition bis Bit 15, Übertrag L entfällt
keine Unterscheidung zwischen „+0“ und „-0“
Größte darstellbare Zahl: LLLL LLLL 0LLL LLLL
alle Bits = L außer Vorzeichenbit = 0:
214 + 213 + ... + 21 + 20 = 215 – 1 = 32767
Kleinste darstellbare Zahl:
Probe: -32767:
Komplement zu 32767: LLLL LLLL 0LLL LLLL
0000 0000 L000 0000
+
1
-32767 :
0000 000L L000 0000
aber: es geht kleiner:
-1
-32768
32768 positive Zahlen (0 ... 32767)
32768 negative Zahlen (-1 ... –32768)
Achtung!!!
Überlauf bei Additionen über den größten darstellbaren Wert
L