IV. Zahlbereichserweiterung

Didaktik der Algebra
M. Ludwig
IV. Zahlbereichserweiterung
5./6. Klasse:
6. Klasse:
7. Klasse:
9. Klasse:
Natürliche Zahlen;nach dem neuen Bildungsplan auch negative ganze Zahlen
Bruchzahlen
Rationale Zahlen
Reelle Zahlen
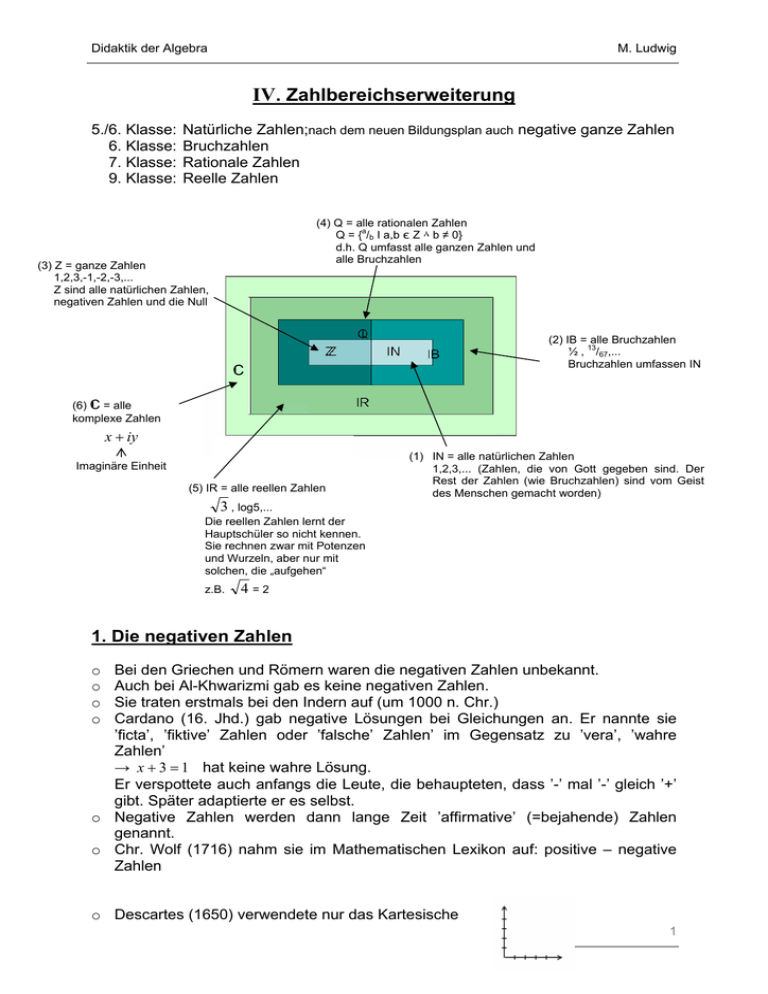
(4) Q = alle rationalen Zahlen
a
Q = { /b I a,b є Z ٨ b ≠ 0}
d.h. Q umfasst alle ganzen Zahlen und
alle Bruchzahlen
(3) Z = ganze Zahlen
1,2,3,-1,-2,-3,...
Z sind alle natürlichen Zahlen,
negativen Zahlen und die Null
(2) IB = alle Bruchzahlen
13
½ , /67,...
Bruchzahlen umfassen IN
C
(6) C = alle
komplexe Zahlen
x + iy
Imaginäre Einheit
(5) IR = alle reellen Zahlen
(1) IN = alle natürlichen Zahlen
1,2,3,... (Zahlen, die von Gott gegeben sind. Der
Rest der Zahlen (wie Bruchzahlen) sind vom Geist
des Menschen gemacht worden)
3 , log5,...
Die reellen Zahlen lernt der
Hauptschüler so nicht kennen.
Sie rechnen zwar mit Potenzen
und Wurzeln, aber nur mit
solchen, die „aufgehen“
z.B.
4=2
1. Die negativen Zahlen
Bei den Griechen und Römern waren die negativen Zahlen unbekannt.
Auch bei Al-Khwarizmi gab es keine negativen Zahlen.
Sie traten erstmals bei den Indern auf (um 1000 n. Chr.)
Cardano (16. Jhd.) gab negative Lösungen bei Gleichungen an. Er nannte sie
’ficta’, ’fiktive’ Zahlen oder ’falsche’ Zahlen’ im Gegensatz zu ’vera’, ’wahre
Zahlen’
→ x + 3 = 1 hat keine wahre Lösung.
Er verspottete auch anfangs die Leute, die behaupteten, dass ’-’ mal ’-’ gleich ’+’
gibt. Später adaptierte er es selbst.
o Negative Zahlen werden dann lange Zeit ’affirmative’ (=bejahende) Zahlen
genannt.
o Chr. Wolf (1716) nahm sie im Mathematischen Lexikon auf: positive – negative
Zahlen
o
o
o
o
o Descartes (1650) verwendete nur das Kartesische
1
Didaktik der Algebra
M. Ludwig
Koordinatensystem (ohne negative Zahlen).
Später wurde es auf unser geläufiges
Koordinatensystem erweitert.
(−1)
1
=
1
(−1)
→ Rechenzeichen und Vorzeichen sind etwas anderes.
o D’Alembert um 1750: (−1) ⋅ (−1) = 1 ⋅ 1 und
1.1. Einführung
o Thermometer:
Besonders beliebtes Bespiel, da es sehr alltagsnah ist;
außerdem ist beim Thermometer der Zahlenstrahl
schon gegeben.
o Guthaben und Schulden:
Ein Lebensbezug ist zwar gegeben, aber die Schüler können
sich nicht so damit identifizieren (ihr Giro-Konto dürfen sie nicht
überziehen und der Kontostand der Eltern wissen sie meist
nicht).
o Fahrstuhl im Kaufhaus:
(Aber häufig steht statt − 1,−2,... U 1, U 2,... )
o Wasserstandsanzeiger:
z.B. ist der Wasserspiegel eines Flusses manchmal über und
manchmal unter dem normalen Pegel.
o Höhenmesser
Ziel: Der Zahlenstrahl wird erweitert!
neu
1.2. Addieren und Subtrahieren negativer Zahlen
z.B.
™ 2+(-3)=?
-3
Der Schüler weiß, dass -3 bedeutet:
auf dem Zahlenstrahl 3 Schritte nach links
→ 2 + (−3) = 1
™ Thermometer: 3°+(-5°)=?
-5°
™
→ Die Temperatur ist um 5° gefallen.
− 2° − 7° = ?
2
Didaktik der Algebra
M. Ludwig
1. Schritt: − 2° + (−7°) = −9°
2. Schritt: − 2° − 7° = −9°
1.3. Multiplikation negativer Zahlen
→ Zurückführung auf Addition:
4 ⋅ (−3) = (−3) + (−3) + (−3) + (−3) = 12
Es gilt:
a ⋅ (−b) = (− a) ⋅ b = −ab
Frage: Was gibt (−3) ⋅ (−4) ?
→ (−3) ⋅ (−4) = 12
1. Erklärung:
Permanenzprinzip: (→ Rechenregeln sollen im neuen Zahlenbereich weiterhin gültig sein)
3 ⋅ (−4) = − 12
+4
2 ⋅ (−4) = − 8
+4
1 ⋅ (−4) = − 4
+4
0 ⋅ (−4) = 0
+4
(−1) ⋅ (−4) = 4
+4
(−2) ⋅ (−4) = 8
+4
(−3) ⋅ (−4) = 12
2. Erklärung:
Distributivgesetz:
− 3⋅
0
=0
− 3 ⋅ (4 + (−4)) = 0
− 3 ⋅ 4 + (−3) ⋅ (−4) = 0
− 12 +
?
=0
→ 0 wird anders geschrieben
→ Distributivgesetz: ausmultiplizieren
⇒ (−3)(−4) = 12
⇒ Wenn unsere bisherigen Rechenregeln gültig bleiben sollen, dann muss
(−a) ⋅ (−b) = a ⋅ b
sein (und zwar für a, b ∈ Q)
3. Erklärung:
5: er verdient 5€ pro Tag
3
Didaktik der Algebra
M. Ludwig
-5: er verliert 5€ pro Tag
3: in drei Tagen
-3: vor drei Tagen
− 5 ⋅ 3 : er verliert jeden Tag 5€. In drei Tagen hat er 15€ weniger.
− 5 ⋅ (−3) : er verliert jeden Tag 5€. Vor drei Tagen war er 15€ reicher. → +15€
(4. Erklärung:)
Umgangssprachlich: Doppelte Verneinung
z.B.
- Es ist heute nicht nicht kalt. → Es ist heute kalt.
- Auf dem PH-Platz beseitigt man die Löcher des Kopfsteinpflasters.
→ Das Kopfsteinpflaster ist vollständig.
Merkregeln:
o ungerade Anzahl an ’-’:Ergebnis ’-’
o gerade Anzahl an ’-’: Ergebnis’+’
o
'+ ' ⋅ '+' = '+ '
'+' ⋅ '−' = '−'
'−' ⋅ '+' = '−'
'−' ⋅ '−' = '+'
o Koordinatensystem:
_
+
+
_
o Kosinus:
++
+
__
2. Die reellen Zahlen
4
Didaktik der Algebra
M. Ludwig
2.1. Einführung
o Wie groß ist x, wennn x²=2?
o Wie groß ist die Seitenlänge eines Quadrates mit dem Flächeninhalt 2?
1
a⋅a = 2
(da
=
)
T2 ⋅ T2 = 2 ( T2 = Tisch 2)
→ Es spielt keine Rolle, welches Zeichen man
a
anfangs einführt oder ob man gleich
d t
2
o Wie lang ist die Diagonale im Quadrat? …
2.2. Näherungsweises Wurzelziehen
Gilt bei einem Näherungsverfahren:
(1) das folgende Intervall liegt im vorhergehenden und
(2) die Intervalllängen werden beliebig klein,
so sagt man, die Intervalle bilden eine Intervallschachtelung.
z.B.
a⋅a = 2
gesucht: a
1²
< a ² < 2²
1²
< a ² < 1,5²
1,25²
< a ² < 1,5²
1,375² < a ² < 1,5²
1,375² < a ² < 1,4375²
2.3. Begründung
2 ist eine irrationale Zahl, d.h. sie ist nicht als Bruch darstellbar.
Beweis: (Widerspruchsbeweis)
Annahme:
2 ist ein Bruch.
p
q
p²
2=
q²
2=
q² ⋅ 2 = p²
( )2
Voraussetzung: ggT ( p, q) = 1
⇒ also ist p² durch 2 teilbar und somit auch p!
⇒ p = 2 p'
5
Didaktik der Algebra
M. Ludwig
q ² ⋅ 2 = (2 p' )²
q ² = 2 p '² ⇒ q² ist durch 2 teilbar und somit auch q!
Widerspruch zur Annahme, dass p und q teilerfremd sind!
q.e.d.
(Hinweis zum Widerspruchsbeweis:
vgl. „Tatort“: „Angenommen A ist der Täter, dann müsste er um 19 Uhr dort gewesen sein,
aber…“
hier:
2=
„Angenommen
p
ist ein Bruch, dann müssen p und q teilerfremd
q
sein…“)
Anderer Beweis: (jetzt: allgemeiner Beweis)
Behauptung:
Annahme:
a ist irrational
a ist rational
p²
p
⇒ a=
⇒ a=
a∈P
q²
q
⇒ p² = a ⋅ q²
PFZ (Primfaktorzerlegung) von p und q
⇒ ( p1 ⋅ p2 ⋅ ... ⋅ pn )² = a ⋅ (q1 ⋅ q2 ⋅ ... ⋅ qm )²
⇒ ( p1 ² ⋅ p2 ² ⋅ ... ⋅ pn ² = a ⋅ q1 ² ⋅ q2 ² ⋅ ... ⋅ qm ²
⇒ p1 ⋅ p1 ⋅ p2 ⋅ p2 ⋅ ... = a ⋅ q1 ⋅ q2 ⋅ ...
p ² ist teilbar durch a .
⇒ p ist teilbar durch a
⇒ q ist auch teilbar durch a
Widerspruch zum Hauptsatz der Zahlentheorie:
„Die Primfaktorzerlegung ist eindeutig!
Exkurs:
Behauptung: Es gibt genau so viele Quadratzahlen wie natürliche Zahlen:
→ Man kann jeder Quadratzahl eine natürliche Zahl zuordnen!
1²
2²
3²
4²
...
1
2
3
4
...
Rechenregeln für irrationale Zahlen
6
Didaktik der Algebra
M. Ludwig
Um die Existenz der reellen Zahlen zu sichern, bettet man sie in den Zahlenstrahl
ein.
Wenn man z.B. den Zahlenstrahl an einer beliebigen Stelle durchschneidet, trifft man
sogar sehr wahrscheinlich nicht auf eine rationale Zahl. Denn zwischen zwei
rationalen Zahlen gibt es unendlich viele irrationale Zahlen.
Irrationale Zahlen lassen sich durch unendliche nicht-periodische Dezimalbrüche
darstellen.
Bsp.:
- 0,10011000111...
n
⎛ 1⎞
- e = lim⎜1 + ⎟
n →∞
⎝ n⎠
- π = 3,141592...
e und π sind Zahlen, die nicht in einer Gleichung darstellbar sind (im Gegensatz
zu a : x ² = a ).
Es wäre zwar möglich: x ² − π ² = 0 , aber dann wird schon die transzendente Zahl
verwendet.
Anschließend müssen die Rechenregeln erklärt werden. Die Rechenregeln gelten
weiterhin. Hinzu kommen Wurzelgesetze,…
Zur Geschichte von
2
Gespräch des Menon mit Sokrates
7