Zählterme (Kombinatorik) - minus-p

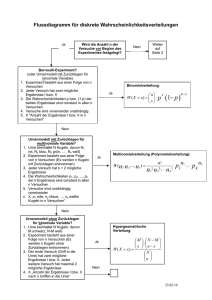
Zählterme (Seite 1)
Bemerkung: „In Mathematik sollte man keine Fahrpläne verwenden, in der
Stochastik erst recht nicht.” Zitat von S.L.
Das Baumdiagramm ist aber fast immer ein geeignetes Hilfsmittel.
Produktregel
Aufgabe: Wie viele Nummernschilder kann es theoretisch im Raum Dresden geben?
Wann müsste die 4.Ziffer eingeführt werden?
Bsp: DD PI-3141
Lösung: 26 $ 26 $ 9 $ 10 $ 10 $ 10 = 6.084.000
Satz (Produktregel): Aus k Mengen M 1 ; M 2 ; ...; M k mit jeweils n 1 ; n 2 ; ...; n k Elementen
kann man n 1 $ n 2 $ ... $ n k verschiedene k-Tupel (x 1 ; x 2 ; ...; x k ) bilden mit x i c M i .
Aufgabe: Wie viele 8-stellige Passwörter kann man bilden, es es aus 6 Groß- und
Kleinbuchstaben und 2 Ziffern zusammengesetzt ist und die Ziffern am Ende
stehen?
Lösung: 52 6 $ 10 2 = 1.977.060.966.400
Aufgabe: Ein Restaurant wirbt mit der Aufschrift „Jeden Tag 420 Menüs“. Jedes
Menü besteht aus einer Vorspeise, einem Hauptgericht, einer Nachspeise und
einem Getränk. 2 Menüs gelten als verschieden, wenn ein Bestandteil verschieden
ist. Sicher ist auch, dass es für jeden Bestandteil Wahlmöglichkeiten gibt.
Wie viele Speisen und Getränke bietet das Restaurant mindestens an?
Zerlegung von 420 = 2 $ 2 $ 3 $ 5 $ 7
kleinste Zerlegung von 420 = 4 $ 3 $ 5 $ 7
Das Restaurant braucht also nur 19 Speisen bzw. Getränke anzubieten.
(1) Geordnete Stichprobe mit Zurücklegen
Aufgabe: Fußballtoto: 31 Spiele werden während der Europameisterschaft getippt.
Sieg (1), Unentschieden (0), Auswärtssieg (2) Wie viele Möglichkeiten gibt es für die
richtige Tendenz?
3 $ 3 $ ... $ 3 = 3 31 = 617.673.396.283.947
Urnenmodell: In der Urne sind n Kugeln und es wird k mal gezogen mit Zurücklegen.
Satz: Die Anzahl der Möglichkeiten, eine geordnete Stichprobe mit Zurücklegen vom
Umfang k aus eine n-elementigen Menge zu entnehmen, beträgt n k .
Aufgabe: Wie groß ist die Wahrscheinlichkeit, dass man eine hexadezimale Zahl
nicht erkennt und irrtümlich als Dezimalzahl interpretiert.
n ... maximale Stellenzahl:
)
P(A ) = ( 10
16
n
Zählterme (Seite 2)
Aufgabe: Beim Morsen verwendet man nur die Zeichen „Punkt“ und „Strich“.
Wie viele Morsezeichen mit höchstens 5 Zeichen sind möglich?
2 5 + 2 4 + 2 3 + 2 2 + 2 1 = 2 6 − 2 = 62
Aufgabe: Berechne die Wahrscheinlichkeit, beim 24-maligen Würfeln mit 2 Würfeln
mindestens einen Sechserpasch zu werfen.
P(A ) =
36 24 −35 24
36 24
) 24 =
= 1 − ( 35
36
671
1296
l 0, 4914
Aufgabe: Berechne die Wahrscheinlichkeit, beim vierfachen Würfelwurf mindestens
eine 6 zu werfen.
671
P(A ) = 6 6−5
= 1296
l 0, 5177
4
2) Geordnete Stichprobe ohne Zurücklegen
4
4
Aufgabe: In einer Liga befinden sich 18 Mannschaften. Wie viele mögliche
Reihenfolgen gibt es, wenn
a) die ersten 3 Plätze betrachtet werden.
b) die gesamte Tabelle betrachtet wird.
Lösung:
18 $ 17 $ 16 = 4896
18! = 6.402.373.705.728.000
Satz: Die Anzahl der Möglichkeiten, eine geordnete Stichprobe ohne Zurücklegen
vom Umfang k aus eine n-elementigen Menge zu entnehmen, beträgt
n $ (n − 1) $ ... $ (n − k + 1). Entnimmt man alle n Elemente, so gibt es n! Möglichkeiten.
(Permutationen)
Urnenmodell: In der Urne sind n Kugeln und es wird k mal gezogen ohne
Zurücklegen.
Festigung:
Begründen Sie folgende Gleichung!
n $ (n − 1) $ ... $ (n − k + 1) = n!
k!
(GTR : nPk )
Beispiel) Staffel
Ein Trainer hat für eine 4x100m-Staffel 6 Sportler zur Verfügung. Wie viele
Möglichkeiten gibt es, wenn wichtig ist, wer an welcher Position läuft?
6$5$4$3=
6!
2!
= 360
Beispiel) Aufstellung
Ein Trainer hat für ein 4-5-1-System 3 Torhüter, 8 Abwehrspieler, 8 Mittelfeldspieler
und 3 Stürmer zur Verfügung. Wie viele Möglichkeiten gibt es für die Aufstellung?
8!
3 $ 8!
4! $ 3! $ 3 = 101.606.400
Zählterme (Seite 3)
Beispiel) Das Geburtstagsproblem
Wie groß ist die Wahrscheinlichkeit, dass in einer Klasse mit 3, 9, 22, 23, 24, 60
Schülern mindestens 2 am gleichen Tag Geburtstag haben?
Es eignet sich folgendes Modell: Urne mit 365 verschiedenen Kugeln mit
Zurücklegen.
Gegenereignis zu A: Alle Schüler haben an verschiedenen Tagen Geburtstag.
P(A) = 365 $ 364 $ 363 = 0, 9918
365 365 365
P(B) = 365 $ ... $9357 = 90, 54%
365
P(A) = 0, 0082 = 0, 82%
P(B) = 9, 46%
$ 344 = 52, 43%
P(C) = 365 $ ... 22
365
$ 342 = 49, 27%
P(D) = 365 $ ... 24
365
P(C) = 47, 57%
P(D) = 50, 73%
$ 342 = 46, 17%
P(E) = 365 $ ... 24
365
$ 306 = 00, 59%
P(F) = 365 $ ... 60
365
P(E) = 53, 83%
P(F) = 99, 41%
In einer Klasse mit 23 Schülern ist es also wahrscheinlich, dass 2 Kinder am
gleichen Tag Geburtstag haben.
(3) Ungeordnete Stichprobe ohne Zurücklegen
Problem: Beim Tippsystem sollen aus 16 Mannschaften 3 ausgewählt werden.
Wie viele Möglichkeiten gibt es, wenn die Reihenfolge keine Rolle spielt?
Wir können das Problem lösen, wenn die Stichprobe geordnet sein soll. Dann gilt:
16 $ 15 $ 14 = 3.360 =
16!
13!
Die Reihenfolge ist aber nicht wichtig. Deshalb gibt es wesentlich weniger
Möglichkeiten. Wie viele Möglichkeiten gibt es, 3 Mannschaften anzuordnen?
3 $ 2 $ 1 = 3! = 6
Jeder Tipp kommt also 6-mal vor, wenn man die Reihenfolge der gezogenen Zahlen
beachten würde. Deshalb muss man mit 6 oder 3! dividieren.
3360
6
=
16!
13!$6!
= 560
Problem: 6 aus 49: 6 Zahlen werden aus 49 gezogen
Wie viele Möglichkeiten gibt es, wenn die Reihenfolge keine Rolle spielt?
Wir können das Problem lösen, wenn die Stichprobe geordnet sein soll. Dann gilt:
49 $ 48 $ 47 $ 46 $ 45 $ 44 = 10.068.347.520 =
49!
43!
Zählterme (Seite 4)
Wenn man aber Lotto spielt, weiß man, dass die Reihenfolge nicht wichtig ist. Es
gibt also wesentlich weniger Möglichkeiten. Wie viele Möglichkeiten gibt es, ein und
denselben Tipp anzukreuzen.
6 $ 5 $ 4 $ 3 $ 2 $ 1 = 120 = 6!
Jeder Tipp kommt also 120 mal vor, wenn man die Reihenfolge der gezogenen
Zahlen beachten würde. Deshalb muss man mit 120 dividieren.
49$48$47$46$45$44
1$2$3$4$5$6
= 13983816 =
49!
6!$43!
Urnenmodell: In der Urne sind n Kugeln und es wird k mal gezogen ohne
Zurücklegen mit einem Griff.
Satz: Die Anzahl der Möglichkeiten, eine geordnete Stichprobe mit Zurücklegen vom
Umfang k aus eine n-elementigen Menge zu entnehmen, beträgt
n
=
k
n!
(n−k)!$k!
.
Bemerkungen:
Man nennt diese Anzahl von Möglichkeiten auch Kombinationen. Die Zahlen werden
auch Binomialkoeffizienten genannt, da sie beim Ausmultiplizieren von Binomen
auftreten. Mit dem GTR kann man die Anzahl der Kombinationen ebenfalls
berechnen.
>
OPTN
PROP
nCr
Beispiele: Wahrscheinlichkeiten im Lotto
6
5
P(”5 Richtige”) =
43
1
49
6
6
4
P(”4 Richtige”) =
43
2
49
6
= 0, 0000184
= 0, 000969
Weisen Sie folgende Gleichungen nach.
n
0
=1
n
1
=n
n
2
=
n(n − 1)
2
n
n
=1
n
n−1
=n
n
n−2
=
n(n − 1)
2
Zählterme (Seite 5)
Beispiel: Die kleine Lea bastelt eine Kette aus 3 roten, 13 gelben und 7 blauen
Kugeln. Wie viele Möglichkeiten gibt es für die Kette?
23!
= 137.287.920
3! $ 13! $ 7!
Beispiel: Unter 200 Losen sind 40 Gewinne und 160 Nieten. Paul kauft genau 10
Lose. Mit welcher Wahrscheinlichkeit erhält er genau 2 Gewinne.
40
2
P(X = 2 ) =
160
8
200
10
l 0, 3098
(4) Ungeordnete Stichprobe mit Zurücklegen
Beispiel: Bei einem Sonderangebot kann man sich eine Kiste (zwölf Flaschen) aus
drei verschiedenen Getränkesorten beliebig zusammenstellen. Wieviele
Möglichkeiten gibt es dafür?
Urnenmodell: 3 Kugeln, 12-maliges Ziehen mit Zurücklegen
Sorten A, B; C
Variante: A IIIIII B II C IIII
n=
(12 + 2 )!
=
12! $ 2!
14
12
= 91
Beispiel: 4 Brüder sollen sich einen Beutel mit 6 gleichwertigen Goldmünzen
aufteilen. Wie viele Verteilungen sind möglich?
Urnenmodell: 4 Kugeln, 6-maliges Ziehen mit Zurücklegen
Variante: A IIIIII B C D
9! =
6! $ 3!
9
6
= 84
Satz: Die Anzahl der Möglichkeiten, eine geordnete Stichprobe mit Zurücklegen vom
Umfang k aus eine n-elementigen Menge zu entnehmen, beträgt
n+k−1
k
.