Beispielaufgaben und Lösungen

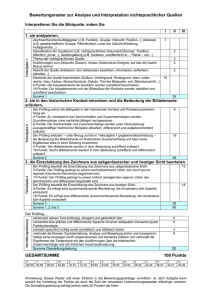
Physik
Informationen für die Hand der Lehrerin/des Lehrers
Grundkurs
Leistungskurs
Jede Prüfungsaufgabe im Fach Physik kann aus bis zu 2 Aufgaben gebildet
sein. Für die Bildung der Prüfungsaufgabe gilt:
•
Die Schule erhält für den Grundkurs und für den Leistungskurs je zwei
Prüfungsaufgaben, von denen die Fachlehrerin/der Fachlehrer eine zur
Bearbeitung für die Schülerinnen und Schüler auswählt.
•
Die Prüfungsaufgaben können die Bearbeitung eines Demonstrationsexperimentes beinhalten. Es handelt sich dabei um Versuche mit gängigen
Experimentalaufbauten. Für den Fall, dass mit einem Experiment quantitative Arbeitsunterlagen während der Prüfung gewonnen werden sollen,
werden ersatzweise Versuchsergebnisse mitgeliefert, damit beim Misslingen eines Experimentes bzw. bei fehlendem Experimentiergerät die erforderlichen Daten zur weiteren Bearbeitung zur Verfügung stehen. Für experimentelle Aufgaben ist eine vorzeitige Bekanntgabe der Aufgabe vorgesehen.
•
Eine Aufgabenauswahl durch die Schülerinnen und Schüler ist nicht vorgesehen.
Für die einzelnen Aufgaben werden lediglich Bewertungspunkte, keine Teilnoten vergeben. Die Notenbildung erfolgt über die Punktzahl der gesamten Prüfungsaufgabe gemäß Nr. III.
Im Folgenden wird als Beispiel eine Prüfungsaufgabe mit 2 Aufgaben bereitgestellt.
-1-
I. Aufgabe
1. Aufgabenart
Aufgabenart
Bearbeitung eines Demonstrationsexperimentes
Durchführung und Bearbeitung eines Schülerexperimentes
Bearbeitung einer Aufgabe, die fachspezifisches Material
enthält:
Beschreibung eines nicht vorgeführten Experiments, Texte
2. Aufgabenstellung
s. Anlage (Vorlage der Prüfungsaufgabe für den Prüfling)
3. Materialgrundlage
•
./.
4. Bezüge zu den 'Vorgaben zu den unterrichtlichen Voraussetzungen für die
schriftlichen Prüfungen im Abitur in der gymnasialen Oberstufe im Jahr
2007
1. Inhaltliche Schwerpunkte
• Ladungen und Felder
• Elektromagnetismus
• Elektromagnetische Schwingungen und Wellen
2. Medien/Materialien
• ./.
5. Zugelassene Hilfsmittel
•
•
•
Physikalische Formelsammlung
Wissenschaftlicher Taschenrechner (ohne oder mit Grafikfähigkeit)
Deutsches Wörterbuch
-2-
6.
Vorgaben für die Bewertung der Schülerleistungen
6.1 Allgemeine Hinweise
Die Bewertung erfolgt anhand des folgenden Bewertungsschemas.
Als Grundlage einer kriteriengeleiteten Beurteilung werden zu erbringende Teilleistungen ausgewiesen, die die mit der jeweiligen Aufgabe verbundenen Anforderungen
aufschlüsseln.
Für komplexere Teilleistungen werden unterschiedliche Lösungsqualitäten exemplarisch ausdifferenziert, um zu verdeutlichen, unter welchen Bedingungen eine bestimmte Bewertung angemessen ist. Die Angaben dienen der Orientierung der Korrektoren und sind nicht als exakte Vorformulierungen von Schülerlösungen zu verstehen.
Der Kriterienkatalog sieht in der Regel die Möglichkeit vor, zusätzliche Teilleistungen
des Prüflings zu berücksichtigen. Die hierbei maximal zu erreichende Punktzahl ist in
Klammern angegeben. Die Höchstpunktzahl für die Teilaufgabe insgesamt kann dadurch nicht überschritten werden.
Die Anordnung der Kriterien folgt einer plausiblen logischen Abfolge von Lösungsschritten, die aber keineswegs allgemein vorausgesetzt werden kann und soll.
Die Teilleistungen werden den in den Lehrplänen definierten Anforderungsbereichen
I bis III zugeordnet, die Klassen von unterschiedlich komplexen kognitiven Operationen definieren, aber noch keine eindeutige Hierarchie der Aufgabenschwierigkeiten
begründen. Dazu dienen Punktwerte, die die Lösungsqualität der erwarteten Teilleistung bezogen auf den jeweiligen Anforderungsbereich gewichten. Die Punktwerte
qualifizieren Schwierigkeitsgrade von Teilleistungen im Verhältnis zueinander. Die
Zuordnungen zu Anforderungsbereichen und Punktwertungen sind Setzungen, die
von typischen Annahmen über Voraussetzungen und Schwierigkeitsgrade der Teilleistungen ausgehen. Die für jede Teilleistung angegebenen Punktwerte entsprechen
einer maximal zu erwartenden Lösungsqualität.
Inhaltliche Leistungen und Darstellungsleistungen werden in der Regel gesondert
ausgewiesen und gehen mit fachspezifischer Gewichtung in die Gesamtwertung ein.
Dabei schließt die inhaltliche Leistung eine sachgerechte Verwendung der Fachterminologie ein. Ausnahmen bilden die Fächer Mathematik, Physik, Informatik und
Technik sowie Griechisch und Latein im Übersetzungsteil, die die Bewertung der
Darstellungsleistung insgesamt in die Bewertung der inhaltlichen Teilleistungen integrieren. Die Entscheidung über eine Absenkung der Bewertung aufgrund von gehäuften Verstößen gegen die sprachliche Richtigkeit (§ 13 Abs. 6 APO-GOSt) wird
wie bisher im Anschluss an die Bewertung der inhaltlichen Leistungen und der Darstellungsleistungen getroffen.
Die folgenden Bewertungskriterien werden in einen für jede Klausur gesondert auszufüllenden 'Bewertungsbogen' aufgenommen, der den Fachlehrerinnen und Fach-
-3-
lehrern zur Verfügung gestellt wird. In diesen trägt die erstkorrigierende Lehrkraft den
entsprechend der Lösungsqualität jeweils tatsächlich erreichten Punktwert für die
Teilleistung in der Bandbreite von 0 bis zur vorgegebenen Höchstpunktzahl ein. Sie
ordnet der erreichten Gesamtpunktzahl ein Notenurteil zu, das ggf. gem. § 13 Abs. 6
APO-GOSt abschließend abzusenken ist.
6.2.1 Modelllösungen I. Aufgabe
a) Für die Energie E0 des elektrischen Feldes des Kondensators gilt E0 =
1
⋅ C1 ⋅ U 02
2
Mit C1 = 2,0⋅10-6 F und U0 = 20,0 V folgt: E0 = 4,0⋅10-4 J
b) Ablauf und Energieumwandlung bei vernachlässigbarer Dämpfung:
Wenn der Schalter in Stellung B gebracht wird, beginnt der Kondensator 1 sich zu
entladen. Die Stärke des Entladestroms in der Spule steigt nach der lenzschen
Regel nur langsam an. Denn der ansteigende Strom erhöht den magnetischen
Fluss in der Spule und dadurch wird in der Spule eine Spannung induziert, die
dem Anstieg des Stromflusses entgegen wirkt, also die anliegende Spannung reduziert. Durch den ansteigenden Entladestrom wird einerseits der Kondensator 2
geladen. Er nimmt einen Teil der Energie (als elektrische Feldenergie) auf, die der
Kondensator 1 abgibt. Im Magnetfeld der Spule wird gleichzeitig - mit dem ansteigenden Entladestrom zunehmend – der andere Teil der vom Kondensator 1
abgegebenen Energie (als magnetische Feldenergie) gespeichert.
Zum Zeitpunkt T/4 hat sich die ursprüngliche Ladung des Kondensators 1 gleichmäßig auf beide Kondensatoren verteilt und die Spannung an beiden Kondensatoren beträgt 10 V. Die elektrische Feldenergie jedes Kondensators beträgt damit
¼ der Startenergie des Kondensators 1. Die restliche Hälfte der Startenergie ist in
der magnetische Feldenergie des Spulenmagnetfeldes vorhanden, die wie die
Stromstärke zu diesem Zeitpunkt maximal ist.
Die nun abnehmende Stromstärke bewirkt eine Verringerung der Stärke des
Magnetfeldes der Spule. Nach der lenzschen Regel wird eine Spannung so induziert, dass die Abnahme des Stromflusses verlangsamt wird. Dadurch fließt der
Strom weiter und der Kondensator 2 wird weiter aufgeladen. Ohne Dämpfung erreicht er zum Zeitpunkt T/2 eine Spannung von 20V und die Anfangsladung des
Kondensators 1. Der Kondensator 1 ist gerade vollständig entladen und seine
Spannung hat mit 0 V den minimalen Wert erreicht.
Die im magnetischen Feld gespeicherte Energie hat sich wieder vollständig in elektrische Energie der Kondensatorfelder umgewandelt. Nun beginnt der Prozess
in umgekehrter Richtung wieder von vorne. Auf diese Weise wiederholt sich der
beschriebene Vorgang von T/2 bis T mit umgekehrter Stromrichtung und entsprechenden Änderungen von Ladungen und Spannungen.
-4-
Ablauf und Energieumwandlung bei Berücksichtigung der Dämpfung:
Die Leitungen und die Spule haben ohmsche Widerstände, durch die bei Stromfluss ein Teil der Energie in Wärme umgewandelt wird. (Zudem wird infolge beschleunigter Ladungen in dem Schwingkreis elektromagnetische Strahlung in den
Raum abgestrahlt. Die Energieabstrahlung dürfte bei der vorliegenden Frequenz
allerdings vernachlässigbar klein sein.) Daher wird die Amplitude der Schwingung, die ein Maß für die Energie der elektromagnetischen Schwingung ist, immer kleiner. Die Energie hat nach Abklingen der Schwingung somit nicht mehr ihren Ausgangswert (s. u.). Der Einfluss der Dämpfung auf die Frequenz der
Schwingung kann vernachlässigt werden, wenn der ohmsche Widerstand des
Schwingkreises klein gehalten werden kann (genauer: R/L muss möglichst klein
gehalten werden!).
c) Ein Teil der Energie, die sich anfangs auf einem Kondensator befand, wird bei
dem Schwingungsprozess in Wärme umgewandelt. Der andere Teil der Energie
verteilt sich auf die beiden Kondensatoren und bleibt im System. Im einfachen
Schwingkreis dagegen ist der Kondensator nach dem Abklingen der Schwingung
vollständig entladen. Die gesamte Energie hat das System über die Wärmeverluste verlassen.
Da beide Kondensatoren die gleiche Kapazität besitzen, verteilt sich die anfangs
vorhandene Ladung Q0 nach Abklingen der Schwingung zu gleichen Teilen auf C1
und C2.
-5-
2
Dann enthält jeder Kondensator die Energie
Mit der Anfangsenergie E0 =
⎛ Q0 ⎞
⎜ ⎟
1 ⎝ 2 ⎠
.
E1 = ⋅
2
C1
1
1 Q02
ist die Gesamtenergie Eω = 2 ⋅E 1= E0 .
⋅
2 C1
2
1
ΔQ 2 , wobei ΔQ die
2C
halbe Ladungsdifferenz auf den Platten ist. Dies liefert für den Kondensator 1 in
1
(Q + q )2 und für den Kondensator 2 die
Bild 2 mit C = C1 = C2 die Energie E1 =
2C
1
2
Energie E2 =
(Q − q ) .
2C
d) Die Energie eines Kondensators berechnet sich aus E =
Bild 2
e) Der Energiesatz lautet unter Vernachlässigung der Dämpfung
(Q + q )2 + (Q − q )2 + L I 2 = const .
2C
2C
2
Dabei bezeichnen die beiden ersten Summanden die in den Kondensatoren gespeicherte elektrische Energie und der dritte Summand die in der Spule gespeicherte magnetische Energie.
Differentiation nach der Zeit liefert
1
1
⋅ (Q + q ) ⋅ q& − ⋅ (Q − q ) ⋅ q& + L ⋅ I ⋅ I& = 0 .
C
C
Wegen I = q& ergibt sich
1
1
⋅ (Q + q ) − (Q − q ) + L ⋅ I& = 0.
C
C
Nochmalige Differentiation liefert
2
2
⋅ q& + L ⋅ I&& = 0 bzw.
⋅ I + L ⋅ I&& = 0 .
C
C
-6-
Mit dem Ansatz I = Iˆ ⋅ sin (ω ⋅ t ) folgt wegen I&& = − Iˆ ⋅ ω 2 ⋅ sin (ω ⋅ t ) nach Einsetzen in
die Differenzialgleichung und Beseitigung des Faktors Iˆ ⋅ sin (ω ⋅ t ) die Gleichung
2
− L ⋅ ω 2 = 0 , d.h. ω =
C
2
2π
bzw. T =
= 2π ⋅ LC / 2 .
LC
ω
Mit L = 0,20 Hy und C = C1 = C2 = 2,0⋅10-6 F folgt für die Schwingungsdauer
T = 2π ⋅ 0,20 ⋅ 10−6 s = 0,0028 s.
Für die Frequenz f gilt dann f =
1
= 355,9 Hz.
T
-7-
6.2.2 Teilleistungen – Kriterien I. Aufgabe
Lösungsqualität
Teilaufga
ben
Anforderung
Anforderungsbereich
Der Prüfling
I.a)
I
1 berechnet die Energie
Der Prüfling
1 zeichnet das Diagramm
3
0
0
I
II
III
3
2 beschreibt die Schwingung
4
3 erläutert die Energieumwandlungen
5
Summe Teilaufgabe I.b)
Der Prüfling
1
I.c)
III
3
Summe Teilaufgabe I.a)
I.b)
II
3
9
0
I
II
III
vergleicht die Restenergie im vorliegenden Fall mit dem gewöhnlichen Schwingkreis
3
2 berechnet die Einzelenergien
3
3
3 vergleicht die Gesamtenergie mit Eo
Summe Teilaufgabe I.c)
Der Prüfling
3
6
0
I
II
III
1 ermittelt die allgemeine Vorschrift für die Kondensatorenergie
I.d)
2
2
bestimmt die Energien beider Kondensatoren in Abhängigkeit
von Q, q und C
Summe Teilaufgabe I.d)
Der Prüfling
4
0
2
4
I
II
III
1 verifiziert den angegebenen Energiesatz
2
2 leitet die Differentialgleichung her
I.e)
3
3 bestimmt die thomsonsche Formel
3
4 bestimmt Schwingungsdauer und Frequenz
2
Summe Teilaufgabe I.e)
2
5
3
Summe 2. Teilaufgaben I.a) – I.e)
11
22
7
Zwischensumme aus 6.2.2:
40 Punkte
-8-
Anlage
(Aufgabe I in der Form, in der sie den Prüflingen vorgelegt wird)
-9-
Aufgabenstellung:
Elektromagnetischer Schwingkreis
In der Skizze ist eine elektrische Schaltung dargestellt, deren Verhalten im Folgenden genauer analysiert werden soll.
Schalter
A
B
L = 0,20H
C2 = 2,0 µF
U0=20,0V
C1 = 2,0 μF
Oszilloskop
Bild 1
a) Berechnen Sie die Energie, die bei der Schalterstellung A in dem Kondensator 1
mit der Kapazität C1 gespeichert ist.
Nach Umlegen des Schalters in die Stellung B zeigt das Oszilloskop eine gedämpfte
elektrische Schwingung. Das System aus den zwei Kondensatoren und der Spule
bildet also einen Schwingkreis.
b) Beschreiben Sie das Zustandekommen und den Verlauf einer vollen Schwingung
u. a. mit Hilfe eines qualitativ richtigen Zeit-Spannungs-Diagramms und eines
Zeit-Stromstärke-Diagramms.
Beschreiben Sie die auftretenden Energieumwandlungen ohne und mit Dämpfung.
c) Wenn die gedämpfte Schwingung zur Ruhe kommt, ist noch ein Teil der anfänglichen elektrischen Energie in Form elektrischer Energie im System vorhanden.
Begründen Sie diese Tatsache und vergleichen Sie sie mit dem Fall des einfachen Schwingkreises, der aus nur einem Kondensator (C1) und der Spule besteht, indem Sie Gemeinsamkeiten und Unterschiede beschreiben.
- 10 -
Berechnen Sie die nach dem Abklingen der Schwingung in den Kondensatoren
verbleibende elektrische Gesamtenergie und vergleichen Sie diese mit der Energie, die in der Schalterstellung A gespeichert war.
d) Bild 2 zeigt die Ladungsverteilung auf den Kondensatorplatten zu einem beliebigen Zeitpunkt bei geschlossenem Schalter B. Mit +Q bzw. –Q wird die Ladung auf
den äußeren Kondensatorplatten bezeichnet, nachdem die Schwingung abgeklungen ist. q bzw. –q ist die während der Schwingung auf den Platten vorhandene zeitlich veränderliche Zusatzladung.
Bild 2
Geben Sie eine Berechnungsvorschrift für die elektrische Energie in den beiden
Kondensatoren in Abhängigkeit von Q, q und C an.
e) Zeigen Sie, dass für das in Bild 2 dargestellte System bei Vernachlässigung der
Dämpfung der Energiesatz lautet:
(Q + q )2 + (Q − q )2 + 1 ⋅ L ⋅ I 2 = const .
2C
2C
2
Durch zweimalige Differentiation und unter Beachtung von q& = I erhält man eine
Differenzialgleichung für die Stromstärke I.
Zeigen Sie mithilfe des Ansatzes I = Iˆ ⋅ sin (ω ⋅ t ) , dass die Lösung der Differenzialgleichung die thomsonsche Schwingungsformel T = 2π LC / 2 liefert.
Berechnen Sie die Schwingungsdauer und die Frequenz für die in Bild 1 angegebenen Daten.
- 11 -
Anmerkungen:
./.
Hilfsmittel:
•
•
•
Physikalische Formelsammlung
Wissenschaftlicher Taschenrechner (ohne oder mit Grafikfähigkeit)
Deutsches Wörterbuch
Bearbeitungszeit für beide Aufgaben zusammen: 255 Minuten
- 12 -
II. Aufgabe
1. Aufgabenart
Aufgabenart
Bearbeitung eines Demonstrationsexperimentes
Durchführung und Bearbeitung eines Schülerexperimentes
Bearbeitung einer Aufgabe, die fachspezifisches Material
enthält:
Beschreibung eines nicht vorgeführten Experiments, Texte
2. Aufgabenstellung
s. Anlage (Vorlage der Prüfungsaufgabe für den Prüfling)
3. Materialgrundlage
•
./.
4. Bezüge zu den 'Vorgaben zu den unterrichtlichen Voraussetzungen für die
schriftlichen Prüfungen im Abitur in der gymnasialen Oberstufe im Jahr
2007
1. Inhaltliche Schwerpunkte
• Elektromagnetische Schwingungen und Wellen
• Quanteneffekte
2. Medien/Materialien
• ./.
5. Zugelassene Hilfsmittel
•
•
•
Physikalische Formelsammlung
Wissenschaftlicher Taschenrechner (ohne oder mit Grafikfähigkeit)
Deutsches Wörterbuch
- 13 -
6.
Vorgaben für die Bewertung der Schülerleistungen
6.1 Allgemeine Hinweise
Die Bewertung erfolgt anhand des folgenden Bewertungsschemas.
Als Grundlage einer kriteriengeleiteten Beurteilung werden zu erbringende Teilleistungen ausgewiesen, die die mit der jeweiligen Aufgabe verbundenen Anforderungen
aufschlüsseln.
Für komplexere Teilleistungen werden unterschiedliche Lösungsqualitäten exemplarisch ausdifferenziert, um zu verdeutlichen, unter welchen Bedingungen eine bestimmte Bewertung angemessen ist. Die Angaben dienen der Orientierung der Korrektoren und sind nicht als exakte Vorformulierungen von Schülerlösungen zu verstehen.
Der Kriterienkatalog sieht in der Regel die Möglichkeit vor, zusätzliche Teilleistungen
des Prüflings zu berücksichtigen. Die hierbei maximal zu erreichende Punktzahl ist in
Klammern angegeben. Die Höchstpunktzahl für die Teilaufgabe insgesamt kann dadurch nicht überschritten werden.
Die Anordnung der Kriterien folgt einer plausiblen logischen Abfolge von Lösungsschritten, die aber keineswegs allgemein vorausgesetzt werden kann und soll.
Die Teilleistungen werden den in den Lehrplänen definierten Anforderungsbereichen
I bis III zugeordnet, die Klassen von unterschiedlich komplexen kognitiven Operationen definieren, aber noch keine eindeutige Hierarchie der Aufgabenschwierigkeiten
begründen. Dazu dienen Punktwerte, die die Lösungsqualität der erwarteten Teilleistung bezogen auf den jeweiligen Anforderungsbereich gewichten. Die Punktwerte
qualifizieren Schwierigkeitsgrade von Teilleistungen im Verhältnis zueinander. Die
Zuordnungen zu Anforderungsbereichen und Punktwertungen sind Setzungen, die
von typischen Annahmen über Voraussetzungen und Schwierigkeitsgrade der Teilleistungen ausgehen. Die für jede Teilleistung angegebenen Punktwerte entsprechen
einer maximal zu erwartenden Lösungsqualität.
Inhaltliche Leistungen und Darstellungsleistungen werden in der Regel gesondert
ausgewiesen und gehen mit fachspezifischer Gewichtung in die Gesamtwertung ein.
Dabei schließt die inhaltliche Leistung eine sachgerechte Verwendung der Fachterminologie ein. Ausnahmen bilden die Fächer Mathematik, Physik, Informatik und
Technik sowie Griechisch und Latein im Übersetzungsteil, die die Bewertung der
Darstellungsleistung insgesamt in die Bewertung der inhaltlichen Teilleistungen integrieren. Die Entscheidung über eine Absenkung der Bewertung aufgrund von gehäuften Verstößen gegen die sprachliche Richtigkeit (§ 13 Abs. 6 APO-GOSt) wird
wie bisher im Anschluss an die Bewertung der inhaltlichen Leistungen und der Darstellungsleistungen getroffen.
Die folgenden Bewertungskriterien werden in einen für jede Klausur gesondert auszufüllenden 'Bewertungsbogen' aufgenommen, der den Fachlehrerinnen und Fach-
- 14 -
lehrern zur Verfügung gestellt wird. In diesen trägt die erstkorrigierende Lehrkraft den
entsprechend der Lösungsqualität jeweils tatsächlich erreichten Punktwert für die
Teilleistung in der Bandbreite von 0 bis zur vorgegebenen Höchstpunktzahl ein. Sie
ordnet der erreichten Gesamtpunktzahl ein Notenurteil zu, das ggf. gem. § 13 Abs. 6
APO-GOSt abschließend abzusenken ist.
6.2.1 Modelllösungen II. Aufgabe
a) Die Reflexion findet an den Netzebenen statt. Der Gangunterschied zweier Wellenzüge, die an benachbarten Netzebenen reflektiert werden, beträgt 2d·sinϑ (vgl.
Bild 2). Es kommt genau dann zu einem ausgeprägten Beugungsmaximum, wenn
2d·sinϑ = n·λ ist. Die Winkel, für die diese Bedingung gilt, heißen Glanzwinkel.
Bild 2
b) In dem Kristallpulver findet man zu allen möglichen Richtungen Netzebenen. Zu
jedem Glanzwinkel ϑ - gegen den einfallenden Elektronenstrahl gemessen - gibt
es daher Mikrokristalle. Bildet ein Mikrokristall mit dem einfallenden Elektronenstrahl einen Glanzwinkel ϑ, so findet im Winkel 2ϑ - gegen die Einstrahlrichtung
gemessen - maximale Verstärkung statt. Räumlich gesehen bilden die vom Kristallpulver ausgehenden Strahlen maximaler Verstärkung Kegelflächen. Auf dem
Schirm ergeben sich für die Maxima konzentrische Kreise.
c) Mit den Bezeichnungen in Bild 1 gilt tan ϑ = R1/L. Auflösen nach ϑ und Einsetzen
in die Braggbedingung liefert
⎛1
⎛1
⎛ 0,0198 ⎞ ⎞
⎛ R ⎞⎞
λ = 2d ⋅ sin ⎜⎜ ⋅ arctan⎜ 1 ⎟ ⎟⎟ = 2 ⋅ 1,23 ⋅ 10−10 m ⋅ sin ⎜⎜ ⋅ arctan⎜
⎟ ⎟⎟ = 1,727 ⋅ 10 −11 m
⎝ L ⎠⎠
⎝ 0,14 ⎠ ⎠
⎝2
⎝2
d) Nach dem Energiesatz ist
1
mv ² = e ⋅ U . Also folgt v =
2
2e ⋅ U
und damit
me
2e ⋅ U
= 2e ⋅ me ⋅ U .
me
Für die Wellenlänge bei einer Beschleunigungsspannung von 5000 V ergibt sich
p = me ⋅ v = me ⋅
- 15 -
λ = h/ p
= 6,626 ⋅ 10 −34 Js / 2 ⋅ 5000V ⋅ 1,602 ⋅ 10 −19 C ⋅ 9,109 ⋅ 10 −31 kg
= 1,734 ⋅ 10 −11 m
Die prozentuale Abweichung beträgt
1,734 − 1,727
≈ 0,6% .
1,734
Die relativistische Rechnung liefert eine Wellenlänge von 1,730·10-11 m. Die Abweichung von der nicht-relativistischen Rechnung liegt bei 0,24%.
Die nicht-relativistische Rechnung war also in dem Sinne berechtigt, dass sie
sehr genaue Näherungswerte liefert.
e) E 2 − c 2 p 2 = E0
2
2
⇒ c 2 p 2 = E 2 − E0 = (E0 + Ekin ) − E0 = 2 E0 ⋅ Ekin + Ekin
2
2
Da Ekin = e ⋅ U ist, folgt c 2 p 2 = 2mec 2eU + (eU )
2
Auflösen nach p liefert die verlangte Beziehung.
- 16 -
2
6.2.2 Teilleistungen – Kriterien II. Aufgabe
Lösungsqualität
Teilaufga
ben
Anforderung
Anforderungsbereich
Der Prüfling
II.a)
I
1 stellt die Reflexion an Netzebenen dar
Der Prüfling
1 beschreibt das Beugungsbild
II.b)
2
5
3
5
0
I
II
III
2
stellt die Bedingung für die Beugungserscheinung dar
3
3 deutet die Intensitätsmaxima
3
Summe Teilaufgabe II.b)
Der Prüfling
II.c)
2
3
3
I
II
III
1 leitet die Gleichung her
3
2 berechnet die Wellenlänge
3
Summe Teilaufgabe II.c)
Der Prüfling
3
3
0
I
II
III
1 bestimmt die Wellenlänge
II.d)
4
2 diskutiert die Abweichungen
3
4
3 rechnet relativistisch
Summe Teilaufgabe II.d)
Der Prüfling
II.e)
III
3
2 bestimmt die Bedingung für den Glanzwinkel
Summe Teilaufgabe II.a)
II
3
8
0
I
II
III
1 leitet den Impuls her
4
Summe Teilaufgabe II.e)
0
0
4
Summe 2. Teilaufgaben II.a) – II.e)
11
19
7
Zwischensumme aus 6.2.2:
37 Punkte
- 17 -
Anlage
(Aufgabe II in der Form, in der sie den Prüflingen vorgelegt wird)
- 18 -
Aufgabenstellung:
Elektronenstrahlbeugung:
De Broglie übertrug die für Photonen gültige Beziehung p = h/λ und damit das Vorhandensein von Welleneigenschaften auf Elektronen. Die Richtigkeit der Beziehung
kann durch Beugungsversuche an Kristallgittern überprüft werden.
a) Entscheidend ist bei der Überprüfung die Braggsche Bedingung 2d·sinδ = n·λ
(Bedingung für Glanzwinkel). Darin bezeichnet d den Netzebenenabstand im
Kristallgitter und δ den Winkel zwischen einfallendem Strahl und Kristallfläche.
Leiten Sie die Braggsche Bedingung her.
b) In einem bekannten Versuch zur Prüfung der Braggschen Bedingung arbeitet
man nach der Methode von Debye-Scherrer. Dabei werden Elektronen durch eine
Spannung U beschleunigt und durch eine aus vielen Kristalliten bestehende Kristallpulverprobe geschickt (siehe Bild 1).
Bild 1
Beschreiben sie das Beugungsbild und begründen sie das Zustandekommen seiner Struktur.
c) R1 bezeichne den Radius des hellen Beugungsringes 1. Ordnung. Man misst für
U = 5000 V einen Wert von R1 = 1,98 cm .
Zeigen Sie: Mit den Bezeichnungen in Bild 1 gilt die Gleichung
⎛
⎛1
⎝2
λ = 2d ⋅ ⎜⎜ sin ⎜ ⋅ arctan
⎝
R1 ⎞ ⎞
⎟⎟ .
L ⎠ ⎟⎠
Berechnen Sie λ, wenn L = 14 cm und d = 1,23·10-10 m ist.
- 19 -
d) Zeigen Sie durch nicht-relativistische Rechnung: Für den Elektronenimpuls gilt
p = 2Ueme .
Welche Wellenlänge liefert das für eine Beschleunigungsspannung U = 5000 V?
Vergleichen Sie mit dem Wert aus c)
Eine relativistische Rechnung liefert für den Impulsbetrag
2
⎛ eU ⎞
p= ⎜
⎟ + 2emeU .
⎝ c ⎠
Welche Wellenlänge ergibt sich nun aus der de Broglie - Beziehung? War die
nicht-relativistische Rechnung berechtigt?
e) In der Relativitätstheorie gilt für eine bewegte Masse folgende wichtige Beziehung
zwischen relativistischer Gesamtenergie E, Impulsbetrag p und Ruhenergie E0:
E 2 − c 2 p 2 = E0
2
Leiten Sie daraus die unter d) angegebene Berechnungsvorschrift für p ab.
Beachten Sie: E = E0 + Ekin = me c 2 + Ekin
Anmerkungen:
./.
Hilfsmittel:
•
•
•
Physikalische Formelsammlung
Wissenschaftlicher Taschenrechner (ohne oder mit Grafikfähigkeit)
Deutsches Wörterbuch
Bearbeitungszeit für beide Aufgaben zusammen: 255 Minuten
- 20 -
III. Prüfungsaufgabe insgesamt:
1. Gesamtsumme der Punkte aus I. und II.:
77 Punkte
2. Grundsätze für die Bewertung (Notenfindung)
Die Zuordnung der Noten (einschließlich der jeweiligen Tendenzen) geht davon aus,
•
•
•
dass die Note ausreichend (5 Punkte) erteilt wird, wenn annähernd die Hälfte
(mindestens 45 %) der Gesamtleistung erbracht worden ist.
dass die Note gut (11 Punkte) erteilt wird, wenn annähernd vier Fünftel (mindestens 75 %) der Gesamtleistung erbracht worden ist.
dass die Noten oberhalb und unterhalb dieser Schwellen den Notenstufen annähernd linear zugeordnet werden.
Daraus resultiert die folgende Zuordnung der Notenstufen zu den Punktzahlen:
Note
Punkte
Erreichte Punktzahl
sehr gut plus
15
74 - 77
sehr gut
14
70 - 73
sehr gut minus
13
66 - 69
gut plus
12
62 - 65
gut
11
58 - 61
gut minus
10
54 - 57
befriedigend plus
9
50 - 53
befriedigend
8
47 - 49
befriedigend minus
7
43 - 46
ausreichend plus
6
39 - 42
ausreichend
5
35 - 38
ausreichend minus
4
30 - 34
mangelhaft plus
3
25 - 29
mangelhaft
2
21 - 24
mangelhaft minus
1
16 - 20
ungenügend
0
0 - 15
- 21 -