Symmetrie Winkelbetrachtungen Kongruenzsätze für Dreiecke

Grundwissen Mathematik
7. Klasse
Grundwissen Mathematik
7. Klasse
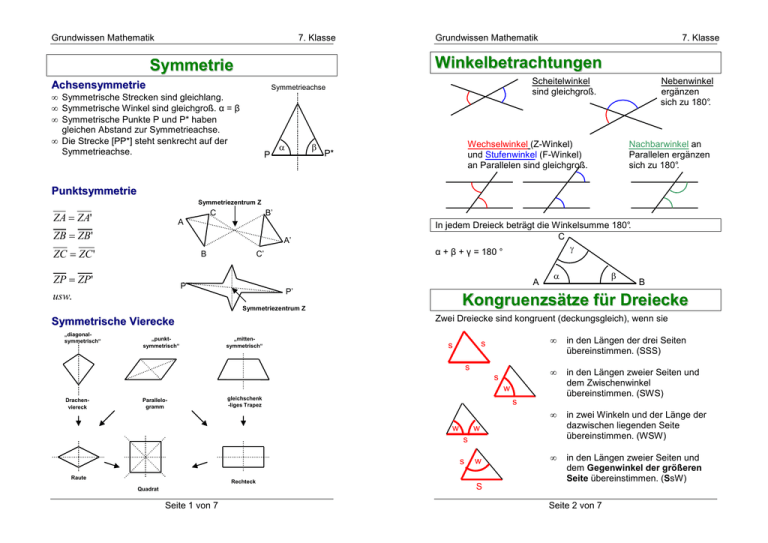
Winkelbetrachtungen
Symmetrie
Achsensymmetrie
Scheitelwinkel
sind gleichgroß.
Symmetrieachse
• Symmetrische Strecken sind gleichlang.
• Symmetrische Winkel sind gleichgroß. α = β
• Symmetrische Punkte P und P* haben
gleichen Abstand zur Symmetrieachse.
• Die Strecke [PP*] steht senkrecht auf der
Symmetrieachse.
P
α
β
Nebenwinkel
ergänzen
sich zu 180°.
Wechselwinkel (Z-Winkel)
und Stufenwinkel (F-Winkel)
an Parallelen sind gleichgroß.
P*
Nachbarwinkel an
Parallelen ergänzen
sich zu 180°.
Punktsymmetrie
Symmetriezentrum Z
C
ZA = ZA'
B’
A
ZB = ZB'
A’
ZC = ZC '
B
ZP = ZP'
C’
In jedem Dreieck beträgt die Winkelsumme 180°.
C
γ
α + β + γ = 180 °
A
P
P
P’
usw.
„mittensymmetrisch“
s
s
s
s
•
in den Längen der drei Seiten
übereinstimmen. (SSS)
•
in den Längen zweier Seiten und
dem Zwischenwinkel
übereinstimmen. (SWS)
•
in zwei Winkeln und der Länge der
dazwischen liegenden Seite
übereinstimmen. (WSW)
•
in den Längen zweier Seiten und
dem Gegenwinkel der größeren
Seite übereinstimmen. (SsW)
w
Drachenviereck
Parallelogramm
gleichschenk
-liges Trapez
s
w
w
s
s
Raute
Rechteck
Quadrat
Seite 1 von 7
B
Zwei Dreiecke sind kongruent (deckungsgleich), wenn sie
Symmetrische Vierecke
„punktsymmetrisch“
β
Kongruenzsätze für Dreiecke
Symmetriezentrum Z
„diagonalsymmetrisch“
α
w
S
Seite 2 von 7
Grundwissen Mathematik
7. Klasse
Grundwissen Mathematik
Satz des Thales
7. Klasse
Besondere Linien im Dreieck
Thaleskreis
C
C
Ein Dreieck ABC hat bei C
90 °
Kathete_
genau dann einen rechten Winkel,
wenn C auf dem Thaleskreis über [AB] liegt.
A
Mittelsenkrechte m
Sie steht senkrecht auf der Seitenmitte.
Kathete
M
Hypotenuse
B
mb
90 ° 90 °
ma
M
Der Schnittpunkt der Mittelsenkrechten
ist der Umkreismittelpunkt M.
90 °
A
mc
Besondere Dreiecke
• Dreiecke mit einer Symmetrieachse
heißen gleichschenklig.
Schenkel_
C
Winkelhalbierende w
Sie halbiert den Innenwinkel und steht
normalerweise nirgends senkrecht.
Spitze
Schenkel
wα
90 °
wβ
W
90 °
Der Schnittpunkt der Winkelhalbierenden
Ist der Inkreismittelpunkt W.
B
90 °
A
B
wγ
Basiswinkel sind gleich groß: α = β
β
α
Basis
60 °
• Dreiecke, bei denen
alle drei Seiten gleichlang sind,
heißen gleichseitig.
Symmetrieachsen!
C
Höhe
Sie geht durch einen Eckpunkt und steht
senkrecht auf der gegenüberliegenden Seite.
b
60 °
Flächeninhalt:
A ∆ = 12 ⋅ Grundlinie⋅Höhe
60 °
A ∆ = 12 a ⋅ h a = 12 b ⋅ h b = 12 c ⋅ h c
Geraden am Kreis
c
90 ° Durchmesser
Das arithmetische Mittel (Durchschnittswert)
Arithmetisches Mittel Summe der Einzelwerte
=
Durchschnittswert  Anzahl der Einzelwerte
M
Bsp.: Mündliche Noten: 2, 1, 3, 2, 1
Tangente
Sekante
B
Durchschnittswert:
2 +1+ 3 + 2 +1 9
= = 1,8
5
5
Seite 4 von 7
a
90 °
ha 90 ° hb
Stochastik
Die Kreistangente steht im Berührpunkt B
senkrecht auf dem Radius.
Passante
Seite 3 von 7
A
hc
90 ° H
B
Grundwissen Mathematik
7. Klasse
7. Klasse
Faktorisieren (Ausklammern)
Terme
Terme sind Rechenausdrücke, die aus Zahlen, Variablen
(Platzhaltern) und Rechenzeichen bestehen. Für die Variablen kann
man unterschiedliche Zahlen einsetzen.
T( x ) = x − 3x
T(2) = 2 − 3 ⋅ 2 = −2
T(−1) = (−1) 2 − 3 ⋅ (−1) = 4
2
Beispiel:
Grundwissen Mathematik
2
Beim Ausklammern werden gleiche Faktoren vor die Klammer
gezogen. Dadurch wird aus einer Summe / Differenz ein Produkt (!).
Beispiele:
2 x + 4 y = 2( x + 2 y )
2abx + 6abc = 2ab( x + 3c)
− 3x − y = (−1) ⋅ (3 + y) = −(3 + y)
− 3a + 3b = −3(a − b)
Terme dürfen nach den Rechengesetzen (KG, AG, DG, Klammerregeln) umgeformt werden, ihr Wert ändert sich dadurch nicht.
Auflösen von Klammern
Bsp:
• Steht vor der Klammer ein Pluszeichen, kann
die Klammer weggelassen werden.
• Steht vor der Klammer ein Minuszeichen, Bsp:
werden beim Auflösen
alle Zeichen in der Klammer umgekehrt:
Aus Plus wird Minus, aus Minus wird Plus.
3x + ( 4 x − 3a ) =
3x + 4 x − 3a =
7 x − 3a
3x − ( 4 x − 3a ) =
3x − 4 x + 3a =
− x + 3a
Multiplizieren / Dividieren von Summen
• Summen (Differenzen) werden mit einem Faktor multipliziert,
indem man jedes Glied der Summe (Differenz)
mit diesem Faktor multipliziert. (DG)
• Genauso: Summen (Differenzen) werden durch einen Divisor
dividiert, indem man jedes Glied der Summe (Differenz) durch
diesen Faktor dividiert.
Beispiele: 2 ⋅ (12 + 4 x ) = 2 ⋅ 12 + 2 ⋅ 4x = 24 + 8x
(12 + 4 x ) ÷ 2 = 12 ÷ 2 + 4 x ÷ 2 = 6 + 2 x
Gleichungen lösen
Gleichungen löst man mit Hilfe von Äquivalenzumformungen.
Das sind Umformungen, bei denen sich die Lösungsmenge der
Gleichung nicht ändert.
Äquivalenzumformungen:
• Zu beiden Seiten wird dieselbe Zahl (oder derselbe Term) addiert.
• Von beiden Seiten wird dieselbe Zahl (oder derselbe Term)
subtrahiert.
• Beide Seiten werden mit dem gleichen Faktor ( ≠ Null) multipliziert.
• Beide Seiten werden durch dieselbe Zahl ( ≠ Null) dividiert.
• Man kann beide Seiten einer Gleichung vertauschen.
Bsp:
+ 7x + 8
− 7 x + 4 = 3x − 8
12 = 10 x
x = 1,2
Lösungsmenge
÷ 10
L = { 1,2
• Zwei Summen werden multipliziert, indem man jeden Summanden
der ersten Klammer mit allen Summanden der zweiten Klammer
multipliziert und diese Produkte dann addiert. („Jedes mit jedem.“)
(a + b) ⋅ (c + d ) = ac + ad + bc + bd
Und: Vorzeichen bzw. Rechenzeichen beachten!
Bsp:
(2x + 3y)(3 − 4x ) = 6x − 8x 2 + 9 y − 12xy
Seite 5 von 7
Seite 6 von 7
}
Grundwissen Mathematik
7. Klasse
Prozentrechnung
Das Ganze, dessen Anteile verglichen werden,
heißt Grundwert (GW).
Ein Anteil am Ganzen wird als Bruch oder als Prozentsatz (p)
dargestellt. % bedeutet „Hundertstel“.
Der jeweilige Teil des Ganzen bildet den zugehörigen
Prozentwert (PW).
Beispiel:
60% von 10kg sind 6 kg.
Prozentsatz Grundwert Prozentwert
Es gilt:
(als Dezimalbruch)
Prozentwert = Prozentsatz · Grundwert (PW= p · GW)
6kg
=
Prozentsatz =
0,6
·
10kg
Prozentwert
Grundwert
(p =
PW
)
GW
Häufige Prozentsätze:
10% =
10
1
=
= 0,10
100 10
25% =
1
1
33 % = = 0,3333333...
3
3
75% =
75 3
= = 0,75
100 4
50% =
25 1
= = 0,25
100 4
50 1
= = 0,50
100 2
100% =
100
=1
100
Beispiel: 30 Kinder wählen einen Klassensprecher. Lorenz erhält 24
Stimmen. Wie viel Prozent der Stimmen sind das?
Grundwert: 30
Prozentwert: 24
Prozentsatz (Anteil in %):
p=
24 4 80
= =
= 80%
30 5 100
Seite 7 von 7