… ein wenig Mechatronik gefällig ?

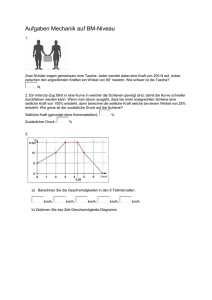
… ein wenig Mechatronik gefällig ?
Aus der Quadrokopter-Projektarbeit ergab sich ( danke für das Interessse ! ) die Frage, wie
man denn die Flugmechanik, und hier insbesondere die Rechnerei mit Integral und
Differerential (auch am PID-Regler) so richtig verstehen kann.
Hier Beispiel zum Mitdenken :
2
Mein 4Copter wiegt 1250 Gramm. Die Erde zieht ihn also mit 1.25 kg * 9.81 m/s nach unten.
Die Motoren sind Roxxy 2827-35, mit EPP1045 Luftschrauben an 3 Lipo-Zellen. Laut Datenblatt bringt das pro
Motor bei Volllast rund 600 Gramm Schub, die Kennlinie ist nahezu linear.
Rechnerisch liegt die Schwebedrehzahl als bei rund 50% der möglichen Leistung, das entspricht der
Flugerfahrung.
Nun machen wir auf dem Papier folgenden Versuch : aus dem Arbeitspunkt (Schwebeflug) einen Sprung auf
75% Motorleistung für 100 ms.
Technische Mechanik :
Wir nähern den kurzen Sprung als lineare Auslenkung um den Arbeitspunkt an. Die erreichten
Geschwindigkeiten des Copters werden also als so gering angenommen, daß der Motorschub nicht dadurch
abgeschwächt wird. (Hab ich mal nachgerechnet, bleibt immer deutlich unter 5 %).
Der Sprung erzeugt (hier wird der Motor als verzögerungsfrei angenommen, für einen Regler dürfte man das
nicht so vereinfachen !) eine Kraftänderung von dF = 6.25 N. Mit a = F/m (aus : Kraft = Masse *
2
Beschleunigung) ergibt das a = 5 m/s
Mathematik / Physik zum Anfassen :
Nun ein Bildchen auf Karopapier zeichnen : nach rechts die Zeit, Auflösung 1 Kästchen = 10 ms, nach oben die
2
Beschleunigung, Auflösung 1 m/s pro Kästchen. Drunter ein zweites, selbe Zeitachse, aber nach oben die
-2
Geschwindigkeit in m/s, Auflösung 5* 10 pro Kästchen.
2
Die Geschwindigkeit ist die Beschleunigung mal der Zeit (v = a * t, oder : m/s = m/s * s ) .
Also oben im Zeitraster einfach immer 10 ms (ein Kästchen der Zeitachse) mit der anliegenden Beschleunigung
2
5 m/s multiplizieren, und nach rechts stetig aufaddieren, weil sich die Geschwindigkeitsänderungen ja
addieren.
–> Gibt eine Rampe, die bei 100 ms auf 0.5 m/s angewachsen ist. Beschleunigung a ist ab da wieder Null, das
Ding wird nicht mehr schneller.
Das ist nix anderes, als die Integralrechnung so vereinfacht, daß man sehen kann was passiert. Eigentlich haben
wir ja eine Differentialgleichung :
http://www2.mpip-mainz.mpg.de/~vollmerd/Vorlesung_SS2012/Kapitel%203%20Mechanik_4_Mai.pdf
(Seite 27)
in der die Geschwindigkeit das Integral der Beschleunigung über die Zeit darstellt. Mathematisch macht man
die Auflösung in der Zeit einfach so klein, daß die Beschleungung auch kurvenförmig sein darf und man das
trotzdem wie oben rechnen kann. Im Mikroprozessor wird aber genau wie oben gerechnet. Man nennt die
Gleichung, wenn Integrale und Differentiale vorkommen „Differentialgleichung“. Wenn das auf nem Prozessor,
also genau wie oben, gemacht wird, die Zeitauflösung also grob bleibt, nennt man das „Differenzengleichung“.
Fertig, mehr ist es nicht ….
Kleine Aufgabe : integrieren Sie im Sinne einer Differenzengleichung die Geschwindigkeit weiter zur Ortsachse !
(Die Physik ist simpel, der Weg ist das Integral über die Geschwindigkeit in der Zeit. Wenn ich nicht irre
kommen 2,5 cm raus)