DOC

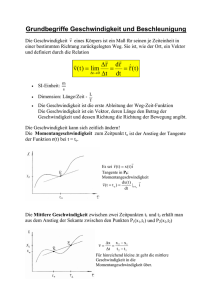
Grundbegriffe Geschwindigkeit und Beschleunigung

Die Geschwindigkeit v eines Körpers ist ein Maß für seinen je Zeiteinheit in
einer bestimmten Richtung zurückgelegten Weg. Sie ist, wie der Ort, ein Vektor
und definiert durch die Relation



 r d r 
v( t )  lim

 r (t)
t 0 t
dt
m
s

SI-Einheit:

Dimension: Länge/Zeit -

Die Geschwindigkeit ist die erste Ableitung der Weg-Zeit-Funktion nach
der Zeit
Die Geschwindigkeit ist ein Vektor, deren Länge den Betrag der Geschwindigkeit und dessen Richtung die Richtung der Bewegung angibt.
L
T
Die Geschwindigkeit kann sich zeitlich ändern!
Die Momentangeschwindigkeit zum Zeitpunkt to ist der Anstieg der Tangente
der Funktion r(t) bei t = to.


Es sei r ( t )  x ( t ) i
Tangente in P0:
Momentangeschwindigkeit


dx ( t )
v( t  t o ) 
|t t o i
dt
Die Mittlere Geschwindigkeit zwischen zwei Zeitpunkten t1 und t2 erhält man
aus dem Anstieg der Sekante zwischen den Punkten P1(x1,t1) und P2(x2,t2)
x x 2  x1

t
t 2  t1
Für hinreichend kleine t geht die mittlere
Geschwindigkeit in die Momentangeschwindigkeit über.
v

Ist die Geschwindigkeit v( t ) eines Körpers gegeben, so kann man die Weg-Zeit
Funktion r ( t ) durch Integration ermitteln:



r ( t )   v( t )dt  rC
oder
t



r ( t )  r0 ( t 0 )   v( t )dt
t0

rC (t ) : Integrationskonstante, wird bestimmt mittels der Anfangsbedingung

r0 ( t 0 )
Beispiel:
geradlinig gleichförmige Bewegung


Für v( t ) = const.= v0 (t ) gilt dann:



r (t )  r0 (t  0)  v 0 t




Da die Größen v ( t ) , v 0 ( t ) und r ( t ) , r0 ( t ) Vektoren sind, erhält man mit




r ( t )  x ( t ) i  y( t ) j  z ( t ) k
und




v( t )  v x i  v y j  v z k
aus obiger Vektorgleichung drei Gleichungen:
x(t) = xo + v0x t ; y(t) = y0 + v0y t ; z(t) = z0 + v0z t

Ist die Funktion v( t ) bekannt, so kann der zeitliche Mittelwert der Geschwindigkeit zwischen zwei Zeitpunkten t1 und t2 auch folgendermaßen berechnet
werden:
t2
v

v
 (t )dt
t1
t 2  t1

x 2  x1 x

t 2  t1
t
Die Berechnung des zeitlichen Mittelwertes der Geschwindigkeit durch Integration führt zum selben Resultat, wie die Berechnung aus dem Anstieg der Sekante.
Beschleunigung

Die Beschleunigung a gibt an, wie schnell ein Körper seine Geschwindigkeit ändert. Sie kann mittels folgender Relation definiert
werden:




v dv 
a ( t )  lim

 v( t )  r( t )
t 0 t
dt
m
s2
L
T2

Si - Einheit:

Dimension:

Die Beschleunigung ist die erste Ableitung der Geschwindigkeits-Zeit-Funktion nach der Zeit
und die zweite Ableitung der Weg-Zeit-Funktion.
Die Beschleunigung ist ein Vektor:
Länge:
Betrag der Beschleunigung
Richtung: Richtung der Beschleunigung
Ist die Beschleunigung gegeben, so kann man die Geschwindigkeit
durch Integration ermitteln:
v
t
v0
t0




d
v

a
(
t
'
)
dt
'

v
(
t
)

v
0 (t 0 )
 
Superpositionsprinzip
Innerhalb eines Bezugssystems gilt das Superpositionsprinzip:
Gleichzeitig ablaufende Bewegungen eines Körpers
beeinflussen sich gegenseitig nicht. Die Bewegungen
können, ohne dass sich am Ergebnis etwas ändert,
auch einzeln nacheinander ablaufen.
Die momentane Geschwindigkeit eines Körpers ergibt sich
aus der vektoriellen Summe der Geschwindigkeiten
der Teilbewegungen.
 n 
v   vi
i 1

v1




vi ( t )  vix i  viy j  viz k

v

v2
Galileitransformation und
Additionstheorem der Geschwindigkeiten
Koordinatensysteme, die sich relativ zueinander mit geradlinig gleichförmiger Geschwindigkeit vr bewegen, heißen Inertialsysteme. Für
diese Systeme gilt im Rahmen der klassischen Mechanik beim Übergang von einem Koordinatensystem in ein anderes Bezugssystem die
Galileitransformation sowie das Additionstheorem der Geschwindigkeiten.
Es seien A und B zwei Systeme, die sich relativ zueinander mit der
konstanten Geschwindigkeit vr bewegen.
Im System A (ungestrichenes System) seien die Koordinaten des
Ortsvektors r mit (x,y,z) bezeichnet.
Im System B (gestrichenes System) seien die Koordinaten des Ortsvektors r’ mit (x’,y’,z’) bezeichnet.
Die Position eines Massenpunktes läßt sich zwischen B und A folgendermaßen umrechnen:
Galileitransformation:
  
r  r ' v r t
Ein Massenpunkt, der bezüglich B die Geschwindigkeit u’ hat, bewegt
sich bezüglich A mit der Geschwindigkeit
Additionstheorem:
  
u  u' vr
Das Additionstheorem folgt sofort aus der Galileitransformation durch
Differentiation mit

 dr
u
dt
und

 dr '
u' 
dt
Es wird deutlich, dass dies so nur gilt, wenn die Zeit t keiner Transformation unterliegt, d.h. t = t’.
Für die Beschleunigung, die Kraft und die Zeit ergeben sich beim
Übergang von A nach B keine Änderungen, d.h. es gilt:
a = a’
;
F = F’
;
t = t’
In Nichtinertialsystemen ( beschleunigten Bezugssystemen ) treten zusätzliche Kräfte, sogenannte Trägheitskräfte auf (Beispiel: Fliehkraft).