44 - Medi
Werbung

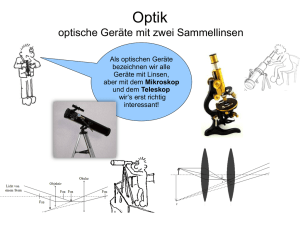
9 Optik 9 Objektträger erzeugt ein reelles, umgekehrtes Zwischenbild. Dieses Zwischenbild betrachtest du durch das Okular, das wie eine Lupe wirkt und ein virtuelles, stark vergrößertes Bild erzeugt (s. Abb. 32). –– den Aperturwinkel α vergrößerst, –– den Brechungsindex n erhöhst (z. B. durch ein Immersionsöl). Der Vergrößerungsmaßstab eines Mikroskops ist das Produkt der Objektivvergrößerung VOb und der Okularvergrößerung VOk: Δ s0 V = Vob ∙ Vok = ∙ fob fok Die Vergrößerung des Okulars kennst du schon von der Lupe. Die Objektivvergrößerung hängt von der Brennweite fOb des Objektivs und der optischen Tubuslänge Δ (s. Abb. 32) ab. Die Welleneigenschaften des Lichts sorgen dafür, dass sich mit einem Lichtmikroskop keine beliebig kleinen Strukturen auflösen lassen. Der kleinste noch trennbare Punktabstand d hängt von der Wellenlänge λ des Lichts, dem Brechungsindex n des Mediums zwischen Objekt und Objektiv und dem Winkel α, unter dem die Objektöffnung vom Objekt aus betrachtet wird, ab: λ λ d= = numerische Apertur n ∙ sinα Du kannst das Auflösungsvermögen eines Lichtmikroskop verbessern, indem du –– Licht mit einer kleineren Wellenlänge verwendest, Aus Kapitel 8 weißt du, dass elektromagnetische Strahlung von Materie absorbiert wird. Wird Licht durch eine Lösung gestrahlt, ist die Absorption abhängig von der Konzentration der Lösung. Dieser Effekt wird in der Photometrie zur Konzentrationsbestimmung von Lösungen genutzt. Gegenstand 9.3 Photometrie 9.3.1 Lambert-Beer-Gesetz Die Extinktion E ist eine logarithmische Größe (Zehnerlogarithmus). Sie ist ein Maß dafür, wieviel Licht von der Probe absorbiert wird: I E = lg 0 I I0 ist die ursprüngliche Lichtintensität, während I die Intensität ist, die hinter der Probe gemessen wird. Das Lambert-Beer-Gesetz besagt, dass die Extinktion von der Konzentration c der Lösung und der Schichtdicke d abhängt: E = ε ∙ c ∙ d Die Proportionalitätskonstante ε ist eine Materialeigenschaft und heißt spezifischer Extinktionskoeffizient. Okular Objektiv Auge Δ FOb FOk FOk FOb Zwischenbild Bild Abb. 32: ­Stahlengänge im Mikroskop 44 medi-learn.de/6-phy-32­