Verwendete Zeichen und Begriffe
Werbung
Verwendete Zeichen und Begriffe
Natürliche Zahlen:
Die Menge der natürlichen Zahlen besteht aus den Zahlen 1,2,3,4,5… und enthält
unendlich viele Elemente:
= {1; 2; 3; ...}
3∈ ℕ
bedeutet, dass 3 ein Element der Menge der natürlichen Zahlen ist
0∉ℕ
-1 ∉ ℕ
aber: ℕ0 {0; 1; 2;...} => 0∈ ℕ0
Zahlenstrahl
Er veranschaulicht die Menge der ganzen Zahlen ℤ.
-5
-4
-2
negative ganze Zahlen
O
Null
1
2
4
5 x
natürliche Zahlen
ℤ = {...; -3 ; -2; -1; 0; 1; 2; 3;...}
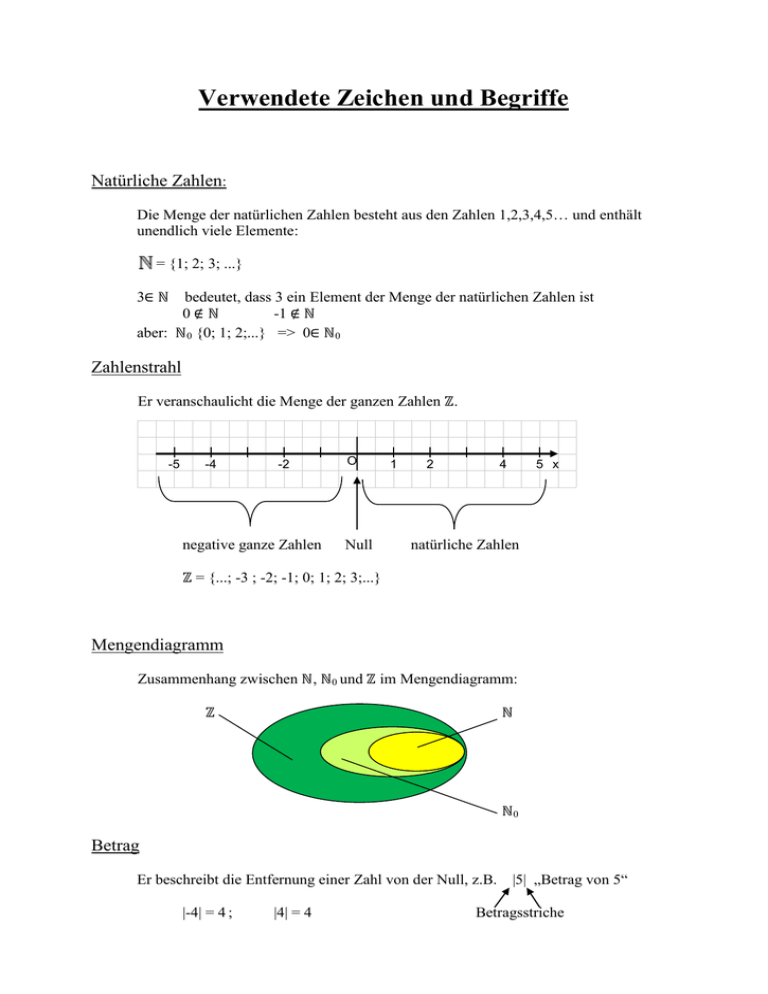
Mengendiagramm
Zusammenhang zwischen ℕ, ℕ0 und ℤ im Mengendiagramm:
ℤ
ℕ
ℕ0
Betrag
Er beschreibt die Entfernung einer Zahl von der Null, z.B.
|-4| = 4 ;
|4| = 4
|5| „Betrag von 5“
Betragsstriche
Begriffe
o Rechenart der Addition
358
+
1.Summand
162
=
520
2.Summand
Wert der Summe
Summe
1.Summand + 2. Summand + 3. Summand + … = Wert der Summe
Redewendung: addiere zu
o Rechenart der Subtraktion
436
-
Minuend
33
=
403
Subtrahend
Wert der Differenz
Differenz
Minuend - 1.Subtrahend = Wert der Differenz
Redewendung: subtrahiere von
o Rechenart der Multiplikation
12
∙
1. Faktor
23
=
2. Faktor
276
Wert des Produkts
Produkt
Faktor ∙ 2. Faktor ∙ 3. Faktor ∙ …
Redewendung: multipliziere mit
=
Wert des Produkts
o Rechenart der Division
558
Dividend
∶
31
Divisor
=
18
Wert des Quotienten
Quotient
Dividend ∶
1. Divisor
=
Wert des Quotienten
Redewendung: dividiere durch
o Potenzrechnung
Exponent
Po-
4
3 = 3 ∙ 3 ∙ 3 ∙ 3 = 3² ∙ 3² = 81
tenz
Basis
o Quadratzahlen: Potenzen mit Exponent 2
5² = 5 ∙ 5 = 25
17² = 17 ∙ 17 =289
o Zehnerpotenz:
4 ∙ 10³ = 4 ∙ 10 ∙ 10 ∙ 10 = 4 ∙ 1000 = 4000
o Primfaktorzerlegung
Primzahlen sind so definiert: Jede Primzahl hat genau zwei Teiler, nämlich 1
und sich selbst.
Bsp.:
5∶1 = 5
und 5 ∶ 5 = 1
, deshalb ist 5 eine Primzahl
Weitere Primzahlen: 2; 3; 5; 7; 11; 13; 17; 19;…
Die 1 gilt nicht als Primzahl.
Alle natürlichen Zahlen außer 1 und Primzahlen lassen sich in Primfaktoren
zerlegen. (siehe Rechenregeln)
Bsp.: 7 = 1 ∙ 7 ;
12 = 2 ∙ 2 ∙ 3 = 2² ∙ 3
36 = 2 ∙ 2 ∙ 3 ∙ 3 = 2² ∙ 3²











