Klasse 6°A a) T = _____ °C b) T = _____ °C c) T = _____ °C d) T

Klasse 6°A
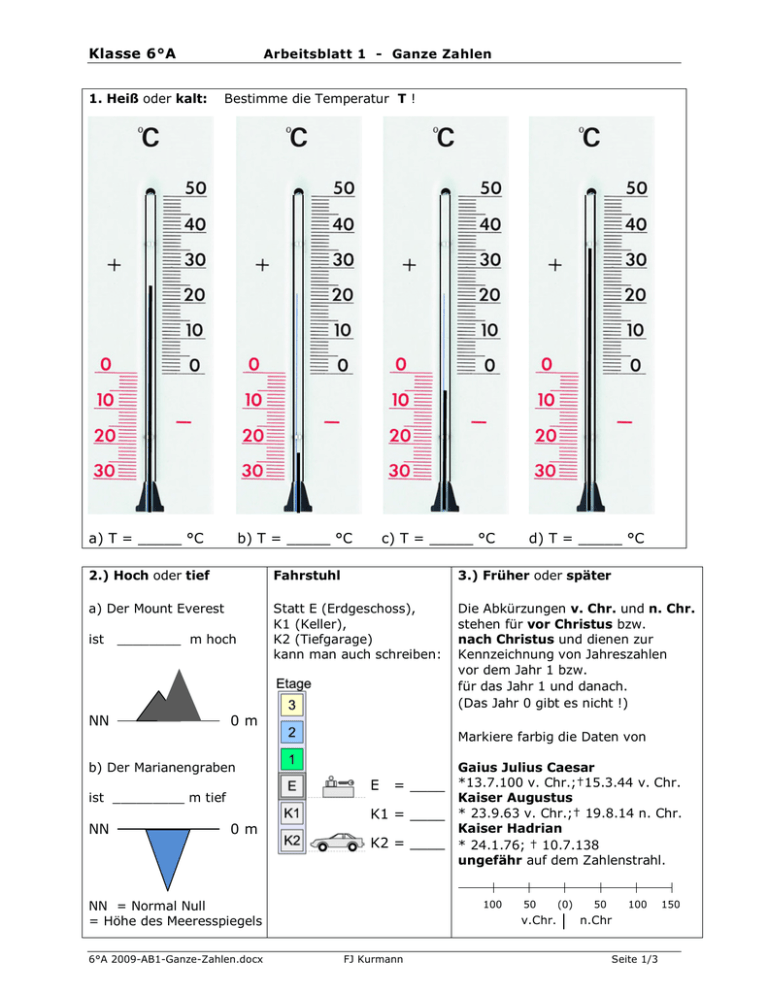
1. Heiß oder kalt:
Arbeitsblatt 1 - Ganze Zahlen
Bestimme die Temperatur T !
a) T = _____ °C
b) T = _____ °C
c) T = _____ °C
d) T = _____ °C
2.) Hoch oder tief
Fahrstuhl
3.) Früher oder später
a) Der Mount Everest
Statt E (Erdgeschoss),
K1 (Keller),
K2 (Tiefgarage)
kann man auch schreiben:
Die Abkürzungen v. Chr. und n. Chr.
stehen für vor Christus bzw.
nach Christus und dienen zur
Kennzeichnung von Jahreszahlen
vor dem Jahr 1 bzw.
für das Jahr 1 und danach.
(Das Jahr 0 gibt es nicht !)
ist
________ m hoch
NN
0m
Markiere farbig die Daten von
b) Der Marianengraben
E
ist _________ m tief
= ____
K1 = ____
NN
0m
K2 = ____
100
NN = Normal Null
= Höhe des Meeresspiegels
6°A 2009-AB1-Ganze-Zahlen.docx
Gaius Julius Caesar
*13.7.100 v. Chr.;†15.3.44 v. Chr.
Kaiser Augustus
* 23.9.63 v. Chr.;† 19.8.14 n. Chr.
Kaiser Hadrian
* 24.1.76; † 10.7.138
ungefähr auf dem Zahlenstrahl.
50
v.Chr.
FJ Kurmann
(0)
50
100
n.Chr
Seite 1/3
150
Klasse 6°A
Arbeitsblatt 1 - Ganze Zahlen
4.) Positiv oder Negativ
bzw.
Plus (+)
oder Minus (–)
Wir müssen offenbar die Zahlengerade der natürlichen Zahlen Í = {1,2,3,4,5,6,7, …}
1
2
3
4
5
6
7
erweitern um die Zahl 0 (Null) und weitere Zahlen unter der Null.
Für Temperaturangaben über Null genügen die bisherigen natürlichen Zahlen.
Zur Beschreibung von Tiefen, Temperaturen unter Null etc. gibt es andere Zahlen. Man
nennt sie negative Zahlen.
Man schreibt die Zahlen unter Null mit einem Minuszeichen, z. B. -3, -5. Zur
deutlichen Unterscheidung zwischen 3 und -3 schreibt man manchmal auch +3 und -3.
Die Zeichen + und - heißen Vorzeichen.
Die Zahlen +3, +5 ... nennt man positive Zahlen.
Die Zahl Null ist weder positiv noch negativ. Sie wird daher ohne Vorzeichen geschrieben.
Positive und negative Zahlen kann man auf einer Geraden anordnen. Man trägt die
positiven Zahlen von Null ausgehend – wie bisher - nach rechts ab.
0
1
2
3
4
5
6
7
5
6
7
Dazu gespiegelt trägt man die negativen Zahlen links von der Null ein.
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
Diese Menge von Zahlen nennt man ganze Zahlen.
Die ganzen Zahlen bilden also die Menge
= {… ,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7, …}
Aufgabe 1: Beschrifte den Zahlenstrahl und markiere die Zahlen auf dem Zahlenstrahl:
a) -3, +4, 0, -7, +7, -1, +3, +6
b) -15, +35, 0, +5, -25, -5, +25, +10
Aufgabe 2: Welche Zahl liegt in der Mitte von:
a) +2 und +10
b) +7 und -5
c) +8 und -4
d) -12 und -4
6°A 2009-AB1-Ganze-Zahlen.docx
FJ Kurmann
Seite 2/3
Klasse 6°A
Arbeitsblatt 1 - Ganze Zahlen
Lösungen
Seite 1
1.) a) T = 25 °C
b) T = –22 °C
c) T = –5 °C
2.) a) Mount Everest: 8848 m hoch,
d) T = 35 °C
b) Marianengraben: 11022 m tief
Fahrstuhl: E = 0 , K1 = –1, K2 = –2
3.)
Gaius Julius Caesar
*13.7.100 v. Chr.;†15.3.44 v. Chr.
Kaiser Augustus
* 23.9.63 v. Chr.;† 19.8.14 n. Chr.
Kaiser Hadrian
* 24.1.76; † 10.7.138
ungefähr auf dem Zahlenstrahl.
100
50
(0)
v.Chr.
50
100
150
n.Chr
Seite 2
1.) a) -3, +4, 0, -7, +7, -1, +3, +6
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
0
5
10
15
4
5
6
7
20
25
30
35
b) -15, +35, 0, +5, -25, -5, +25, +10
-35
2.) a) 6
30
b) 1
-25 -20
c) 2
-15
-10 -5
d) -8
6°A 2009-AB1-Ganze-Zahlen.docx
FJ Kurmann
Seite 3/3