1 Kapitel 10 Stetige Zufallsvariablen und ihre Verteilungen Letzte

1
Kapitel 10 Stetige Zufallsvariablen und ihre Verteilungen
Letzte Änderung: 17. Mai 2000, 20 Seiten
Den folgenden speziellen Verteilungen liegt immer eine stetige Zufallsvariable X zugrunde.
X: Ω → R
1 Die stetige Gleichverteilung
Seien a,b∈R. Eine Zufallsvariable X mit der Dichte
f:[a,b] → R mit
1
f(x) :=
, -∞ < a ≤ x ≤ b < ∞
b-a
heißt gleichverteilt auf dem Intervall [a,b].
Die Verteilungsfunktion ist offensichtlich eine Gerade, wie durch direkte Integration
gezeigt werden kann:
x-a
F(x) =
, -∞ < a ≤ x ≤ b < ∞
b-a
Eine Kurzschreibweise ist X ~ U(a,b).
1
F(x)
f(x)
0
a
b
Das Schema der stetigen Gleichverteilung U(a,b), Dichte und Verteilung
2
2 Die Dreiecksverteilung (Zelt-Verteilung)
Seien a,b,c∈ R. Eine Zufallsvariable X mit der Dichte
ah
hx
+
, 0 ≤a ≤ x≤ b
a-b b-a
ch
hx
f:[a,c] → R mit f(x):=
+
, b< x ≤ c
c-b b-c
0
, sonst
heißt dreiecksverteilt auf dem Intervall [a,c].
Dabei sind die Konstanten a, c, h so zu wählen, daß das Dreieck die Fläche 1 aufweist,
h ⋅(c – a)
Die Fläche unter dem Zelt ist
, hängt also nicht von b ab. Sei z.B. a=0, b=0.5, c=1
2
und h=2, d.h.
0 + 4x , 0 ≤ x ≤ 12
f(x):= 4 - 4x , 21 < x ≤ 1
0
, sonst
Dann ist die Verteilungsfunktion gegeben durch
0
,x <0
2
F(x) = 2x
, 0 ≤ x ≤ 21
4x - 2x2 - 1 , 21 < x ≤ 1
3
Beispiel: Eine weitere Dreiecksdichte
1-|x| if |x| ≤ 1
f(x) =
0 if |x| > 1
{
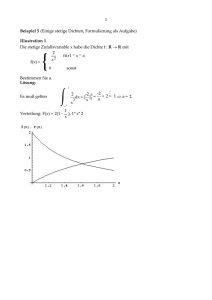
Beispiel (Aufgabe zur Dichte)
Bestimmen Sie zu der folgenden Dichte f die Verteilungsfunktion F:
1
- x ,-2≤x≤0
4
f(x) = x -2 ,2≤x≤3
0
,sonst
Beispiel (Aufgabe zur Transformation)
Sei X eine Zufallsvariable mit der Dichtefunktion
2x, 0<x<1
f(x) =
0, sonst
{
Bestimmen Sie die Dichtefunktion und die Verteilungsfunktion der Zufallsvariablen
Y: = X und skizzieren Sie beide Funktionen.
Lösung
1
1
x2
Um zu prüfen, ob f(x) überhaupt eine Dichte ist, integriere man: 2 xdx = 2⋅
= 1.
2
0
0
Aus der Verteilung F(x) = P[X ≤ x] = x2 folgt dann
P[X ≤ x] = x2 ⇒ P( X≤ x ) = y4 ⇒ P(Y≤y) = y4 ⇔ F(Y≤y) = y4 = F(y), y∈ [0,1], f(y)= 4y3,
da y = x , und x= 0 ⇒ y=0 und x = 1 ⇒ y = 1.
4
3 Die Pareto-Verteilung
Seien a,b ∈ R. Eine Zufallsvariable X mit der Dichte
a b a+1
f:[a,b] → R
f(x):= ( )
für 0<a, 0<b<x
b x
und der Verteilungsfunktion
für x ≤ b
F(x) = 0
a
b
1 - x für 0 < a, 0 <b < x
heißt Pareto-verteilt mit den Parametern a und b.
1
Mit der Variablentransformation u:=
folgt aus der Verteilung F(x) direkt die Dichte
x
durch Ableitung und umgekehrt folgt durch Integration aus der Dichte f(x) die
Verteilung F(x), die beide allen Anforderungen einer Dichte bzw. Verteilung genügen.
Typischerweise sind Einkommen Pareto-verteilt. Zwei Parametrisierungen zeigt die
folgende Abbildung:
2.0
f(x)
1.5
a = 2.0
b = 1.0
1.0
a = 0.5
b = 1.0
0.5
0.0
1
2
3
Zu weiteren Einzelheiten siehe man das Stichwort “Pareto”.
4
x
5
4 Die Exponentialverteilung
Eine Zufallsvariable X mit der Dichte und der Verteilungsfunktion
für x ≤ 0
f(x) = 0 λ für x ≤ 0 bzw. F(x) = 0
x
λe für 0 < x
1 -e -λx für 0 <x
heißt exponentialverteilt mit Parameter λ. Der Parameter λ erfüllt die Bedingung
f(x)
λ = r(x):=
= const.>0
1-F(x)
Eine Kurzschreibweise ist X ~ P(1,λ).
Die Dichten für die Parameter λ=1, λ=3 und λ=5 sehen folgendermaßen aus:
λ=5
f(x)
λ=3
λ=1
x
Anwendung aus der Theorie der Zuverlässigkeit (eine Hauptanwendung):
Sei X, etwa die Brenndauer einer Glühbirne, exponentialverteilt und sei A das
Ereignis, daß X mindestens t0 (t0>0) sei, und sei B das Ereignis, daß die Glühbirne über
t0 hinaus noch bis zum Zeitpunkt t1 (t1>t0) weiterarbeitet.
Interessiert man sich nun für die Wahrscheinlichkeit, daß eine Glühbirne, nachdem
sie schon bis zum Zeitpunkt t0 gebrannt hat, auch noch bis zum Zeitpunkt t1
weiterbrennt, d.h. für die bedingte Wahrscheinlichkeit
P(B∩A)
P(B|A) =
,
P(A)
dann erhält man für die Ereignisse
A (Funktionszeit bis mindestens t ): P(A) = e -λt0,
0
A ∩B (Funktionszeit von t 0 bis t1):
P(A ∩B) = e -λt1,
weil t1 nur erreicht werden kann, nachdem t0 erreicht worden ist. Damit gilt:
6
e-λ t1
P(B|A) =
= e- λt1 + λt0 = e- λ(t1-t0).
e-λt0
Dieses Ergebnis wird üblicherweise als die Gedächtnislosigkeit der Exponentialverteilung bezeichnet. Es kommt nur auf die Zeitdifferenz an, nicht jedoch wo diese
Zeitdifferenz anfällt.
Anwendungsbereiche dieser Verteilungen sind etwa: Die Lebensdauer von Glühbirnen oder anderen technischen Aggregaten oder die Servicezeit an Schaltern. Sie
werden typischerweise durch Exponentialverteilungen beschrieben.
Auch die Sterbewahrscheinlichkeit von Säuglingen wird durch eine ExponentialVerteilung beschrieben.
Zu weiteren Einzelheiten siehe man das Stichwort “Exponential” bzw. “Reliability”.
5 Die Erlang-Verteilung
Eine erste Verallgemeinerung der Exponentialverteilung ist die zweiparametrige
unimodale Erlangverteilung.
Eine Zufallsvariable X mit der Dichte
für x ≤ 0
f: R→R
f(x):= 0
-λx
e
x n-1 λn
für 0 < x
(n-1)!
mit n∈N und λ>0 heißt Erlang-verteilt mit Parametern λ und n.
Eine Kurzschreibweise ist X ~ P(n,λ).
Dichten mit den Parametern λ=3 und n=3 bzw. n=6 sehen folgendermaßen aus:
1
f(x)
λ=3
n=5
0,5
λ=3
n=6
0
1
2
3
4
Für n=1 ist die Exponentialverteilung zurückgewonnen.
x
7
6 Die Weibull-Verteilung
Eine zweite Verallgemeinerung der Exponentialverteilung ist die zweiparametrige
unimodale Weibull-Verteilung.
Eine Zufallsvariable X mit der Dichte
für x ≤ 0
f: R→R
f(x):= 0
λ n
nxn-1λe - x für 0 < x
mit n∈N und λ>0 heißt Weibull-verteilt mit den Parametern λ und n.
Eine Dichte mit den Parametern λ=0.25 und n=2 bzw. n=4 sieht folgendermaßen aus:
f(x)
λ = 0.25
n =4
10
λ = 0.25
n =2
0
1
2
3
4
Für n=1 ist die Exponentialverteilung zurückgewonnen.
5
6
x
8
7 Die Hyper-Exponentialverteilung
Eine dritte Verallgemeinerung der Exponentialverteilung ist die Hyper-Exponentialverteilung:
Eine Zufallsvariable X mit der Dichte
0
für x ≤ 0
n
n
a =1
f: R→R
f(x):=
∑ aiλi e-λ ix für 0 <x mit λi>0 und ∑ i , n∈N.
i=1
i=1
heißt hyper-exponential-verteilt mit Parametern ai und λ i .
Für n=1 folgt erneut die Exponentialverteilung. Hyper-Exponential-verteilte
Zufallsvariable sind sozusagen Mischungen von Exponentialverteilungen. Ein
numerisches Beispiel ist
1- F(x) = p e-λ 1 x + (1 - p) e -λ 2 x ; p = 0.294; λ 1 = 0.541; λ 2 = 0.009, x>0
allgemein 0 < p < 1, d.h.
f(x) = p λ 1 e-λ 1 x + (1 - p) λ 2 e-λ 2 x, 0<x
9
8 Die beidseitige Exponentialverteilung
Eine vierte Verallgemeinerung der
Exponentialverteilung.
Eine Zufallsvariable mit der Dichte
f: R→R
λ +λx
e
,x ≤ 0
2
f(x) :=
λ>0
λ -λx
e
,x > 0
2
Exponentialverteilung
ist
die
beidseitige
heißt beidseitig exponentialverteilt mit Parameter λ.
Dichten mit den Parametern λ=1,2,3 sehen folgendermaßen aus:
f(x)
λ=3
λ=2
λ=1
−1
0
1
x
10
9 Die Cauchy-Verteilung
Eine Zufallsvariable X mit der Dichte
k
f: R→R
f(x):=
, 0<k, - ∞ < x < ∞
2
π⋅(k + (x-m) 2)
heißt Cauchy-verteilt mit Parametern k und m.
Das Maximum der Dichte liegt in x=m:
11
Eine zweite Parameter-Variation von k wird durch die folgenden Abbildungen
gegeben (eine Variation der Cauchy für (m,k): 0,1; 0,2; 0,3)
12
10 Die t-Verteilung (Students t-Verteilung)
Eine Zufallsvariable T mit der Dichte
Γ( n+1 )
2
f: R→R
f(t):=
, -∞ < t< ∞
2 n+1
t
n
πn Γ( ) + (1 + n )
2
heißt t-verteilt mit n Freiheitsgraden.
Der Parameter n wird als Freiheitsgrad der Verteilung bezeichnet.
1
Mit n=1 und Γ( ) = π folgt aus der t-Verteilung die Cauchy-Verteilung mit k=1.
2
Es ist eine unimodale Dichte, die z.B. mit n=5 bzw. n=9 Freiheitsgraden folgendermaßen aussieht:
n=9
0,3
0,2
n=5
0,1
-3
-2
-1
0
1
2
3
13
11 Die Beta-Verteilung
Eine Zufallsvariable mit der Dichte
Γ(α+β)⋅x α-1⋅(1-x) β-1
0 < α,β, 0 <x < 1
f: R→R
f(x): =
Γ(α)⋅Γ(β)
0
sonst
heißt beta-verteilt mit Parametern α und β.
Dabei ist Γ(z) die Gammafunktion
∞
z-1 -x
Γ(z) :=
x e d x , 0 < z, 0 ≤ x < ∞
0
Die Beta-Dichte ist eine zentrale Größe. Aus ihr folgen zahlreiche andere Dichten:
12 Die Fishersche F-Verteilung
Eine Zufallsvariable X mit der Dichte
f +f
Γ( 1 2 )⋅f1f1/2⋅f2f2/2⋅xf1/2-1
2
f: [0,∞ ) → R f(x):=
, f1, f2 ganzzahlig, , 0 ≤ x <∞
f1
f2
(
f
+f
)/2
Γ( 2 )⋅Γ( 2 )⋅(f1 + f2x) 1 2
heißt F-verteilt mit Parametern f1 und f2.
f(x)
0,8
f 1 = f 2 = 10
0,7
f1 = f2 = 6
0,6
f1 = f2 = 4
0,5
0,4
0,3
0,2
0,1
0
1
2
x
Mit f1 = 1, f2 = f sowie x = t 2 ist die F-Dichte die t-Dichte.
Mit α =: f 1/2, b =: f 2/2, F:= (f 1/f2)[x/(1-x)] und f1, f2 ganzzahlig ist die F-Verteilung ein
Sonderfall der Beta-Verteilung.
Man beachte den Zusammenhang zur Binomialverteilung (den Rollentausch von
Variablen und Parametern), d.h.: mit ganzzahligen α und β und x als Parameter erhält
man die Binomial-Verteilung.
14
13 Die Gamma-Verteilung
Eine Zufallsvariable X mit der Dichte
f: (0,∞) → R
f(x) :=
x
α-1 -x/β
e
, 0 < α,β , 0 < x < ∞
α
β Γ(α)
heißt gamma-verteilt mit Parametern α und β.
Die Kurzschreibweise ist X ~ G(α,β).
14 χ 2(Chi-Quadrat)-Verteilung
Eine Zufallsvariable mit der Dichte
f: [0,∞) → R
f(x) :=
x
γ /2-1 x/2
γ /2
e
,0< γ,0≤x< ∞
2
(γ/2-1)!
heißt χ 2(Chi-Quadrat)-verteilt mit Parameter γ.
Der Parameter γ wird als Freiheitsgrad bezeichnet.
Die Kurzschreibweise ist X ~ χ 2 (γ).
Damit gilt im Vergleich zur Gammadichte die Umparametrisierung
χ 2(γ) = G(γ/2,2) bzw. χ 2(2α) = G(α,2)
f(x)
γ=6
1
γ=10
0,5
0
5
10
15
x
Die χ 2-Verteilung kann auch aus der F-Verteilung heraus, d.h. aus der BetaVerteilung spezialisiert werden: Man wähle x:= χ 2 := x/γ, γ := f1 und f2 → ∞.
15
15 Die Weibull-Gamma-Verteilung
Eine Zufallsvariable X mit der Dichte
bkdxb-1
f(x): =
(xb
k+1
,0<b,d,k,0 ≤ x
+ d)
0
,x < 0
heißt Weibull-Gamma-verteilt mit Parametern b, d und k.
Ein erster Sonderfall ist die sog. Burr-Dichte f(x) mit d=1:
bkxb-1
f(x): =
k+1
(xb)
0
, 0<b,k, 0 ≤ x
,x< 0
Ein zweiter Sonderfall ist (s.o.) die Pareto-Dichte f(y) mit d=b=1 und y:=1+x:
k
, 1≤ y
f(y): = y k+1
0 ,y < 1
16
16 Übersicht über den Zusammenhang der stetigen Verteilungen
t-Verteilung
F-Verteilung
χ2
CauchyVerteilung
Beta-Verteilung
Gamma-Verteilung
-Verteilung
Erlang-Verteilung
Doppelt
Exponentialverteilung
Hyper
Exponentialverteilung
Normalverteilung
gestutzte
Normalverteilung
bivariate
Normalverteilung
Exponentialverteilung
Weibullverteilung
Lognormalverteilung
Gleichverteilung
Weibull-Gamma-Verteilung
ParetoVerteilung
BurrVerteilung
17
17 Aufgaben
Aufgabe 1
Zeigen Sie, daß die folgende doppelt exponentielle Funktion als Verteilung dienen
kann:
-x
P[X ≤ x] = F(x) = e-e .
Bestimmen Sie einen geeigneten Definitionsbereich.
Lösunghinweis: Diese Verteilung heißt Extremwertverteilung; es ist eine Verteilung
ohne Parameter (the extreme value distribution) mit der Dichte und einer unimodalen Gestalt:
f(x) = e-x e-e -x , x∈(-∞, +∞)
Eine in der Struktur ähnliche Variable X (d.h. ohne Parameter) ist die folgende (vgl.
Mathematics of Operations Research 1989, 356)
F(x) = (1 - e-x)2, 0≤ x < ∞, f(x) = 2(1 - e-x )e-x
F(0) = 0, F(∞) = 1
Aufgabe 2
Zeigen Sie, daß f(x) = xe-x und F(x) = 1-(1+x)e-x, 0<x<∞ als Dichte und Verteilung
angesehen werden können. Wie beurteilen Sie diese parameterfreie Form?
Aufgabe 3
Bestimmen Sie die Parameter a und b derart, daß die im folgenden aufgeführte beidseitig exponentielle Funktion als Dichte dienen kann:
f(x):= {
ae
be
ax
bx
, x≤0
, x>0
.
18
Aufgabe 4
Zeigen Sie, für welche Spezifikation von α und β die folgende Funktion, die Logistik,
als Verteilung dienen kann.
1
F(x) =
, 0<x<∞,0<α, 0<β .
1 + e-(α+βx)
Zu Illustration betrachte man die Dichte und Verteilung:
f(x) =
ex–10
(1 + ex–10)2
e1.75a , F(x) =
1
1 + ex–10+1.75a
Aufgabe 5
1
, a ≥0, n= 1,2,3,... eine diskrete Verteilungsfunktion
a+n
1
und die zugehörige Zähldichte f(n) =
ist.
(a + n) (a+n - 1)
Zeigen Sie, daß F(n) = 1 -
Aufgabe 6
Die Stutzung einer Verteilung: Sei eine Zufallsvariable X beliebig über dem Intervall
[a1,b1] verteilt und sei A das Ereignis,daß X auf ein Teilintervall[a2,b2], a1≤a2, b2≤b1
eingeschränkt sei.
Zeigen Sie , daß, falls F(x) eine Verteilung über [a1,b1] ist, F(x|A) eine Verteilung über
F(x) -F(a 2)
[a2,b2] ist und F (x|A) =
.
F(b 2) - F( a2)
Aufgabe 7
Zeigen Sie, daß die Funktionen f(.) als Dichte geeignet sind und überprüfen Sie die
Funktionen auf Unimodalität und Symmetrie:
1
(1)
f(x) =
, n=1,2,3,…,, 0<x<n
π x⋅(n - x)
1
(1)’
f(x) =
, 0<x<1
π x(1-x)
die sog. Arcus-Sinus Dichte mit der Verteilung (vgl. Feller II, 49-50)
2
2
x
F(x) = arcsin x , 0<x<1, bzw. F(x) = arcsin
, 0<x<n;
π
π
n
2
(2)
f(x) =
, 0<x<1
2
π 1 –x
2
(mit E(X) = 2/π; F(x) = arc sin x, 0<x<1; vgl. Feller II, 30)
π
19
Aufgabe 8
Zeigen Sie daß die folgenden Funktion jeweils als Dichte dienen können:
1 -(x - 1)2
3
a) f(x) =
, 0 < x< ∞; b) f(x) = 2
, 0 ≤ x ≤2; c) f(x) = (1 - x 2), 0≤x≤1
4- π
2
π(1+x2)
Die folgenden Abbildungen zeigen jeweils die Dichte in der Reihefolge a) b) c)
2
1-
20
f
1-F
(i) Die Ausfallrate für die Zufallsvariable X aus dem Ereignisraum 0<x ist allgemein
f(x)
f(x)
F(x+∆) – F(x) 1
=
= lim
(eine bedingte Dichte), damit folgt:
∆
1 - F(x) P(X>x) ∆→ 0
P(X>x)
18 Ein Sonderproblem: Die Ausfallrate (im Englischen: hazard rate)
F(x+∆) – F(x)
= F(x+∆) - F(x) = P[Ein Ereignis passiert in in (x,x+∆] ] = P[x≤X≤x+∆]
∆
F(x+∆) – F(x)
(ii) P[Ein Ereignis passiert in in (x,x+∆] ] = ∆f(x) = lim ∆
= P[x≤X≤x+∆]
∆
∆→ 0
∆
(iii) Die Beschreibung durch die Verteilung auf drei aufeinander folgenden Intervallen
A, B, C; A:= [0,x], B:= (x,x+∆], C:= (x+∆, ∞), sei E ein beliebiges Ereignis
“Das Ereignis passiert in [0,x]” ∪ “Das Ereignis passiert in in (x,x+∆]” ⇔ E∈(A ∪ B),
A ∩ B = ø ⇔ A ∪ B, A ∩ B = ø, ∴ P(A ∪ B) = P(A) + P(B)
P(A) = F(x) und P(B) = F(x+∆) - F(x)
“Das Ereignis passiert in (x, ∞)”
= “Das Ereignis passiert in (x,x+∆]” ∪ “Das Ereignis passiert in (x+∆, ∞)”
⇔ E∈ A ⇔ E∈B ∪ C,
B ∩ C = ø, ∴ P( A ) = P(B) + P(C) = (F(x+∆) - F(x)) + (1 -F(x+∆)) = 1 - F(x)
“Das Ereignis passiert in [0,x+∆]” ⇔ E∈(A ∪ B)
P(A∪B) = P(A) + P(B) = F(x) + (F(x+∆) - F(x)) = F(x+∆)
P(B ∪ A ) = P(B) + P( A ) - P(B∩ A ) = P(B) + P( A ) - P(B) = 1- F(x) ⇒
P(B∩ A ) = (F(x+∆) - F(x)) + (1- F(x)) - (1- F(x)) = F(x+∆) - F(x)
(iv) Man betrachte das bedingte Ereignis der Ausfallrate:
P(Das Ereignis passiert in (x,x+∆] | Das Ereignis ist in [0,x] nicht passiert), d.h.
ein Ereignis passiert in (0,x+∆]
P(B∩A) F(x+∆) – F(x) ∆
f(x)
P(B|A ) =
=
⋅ , lim P(B|A) =
∆ ∆→ 0
P(X>x)
1 - F(x)
P(A)
Zu weiteren Einzelheiten siehe man das Stichwort “Hazard rate”