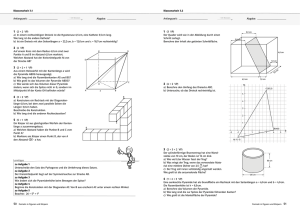
Aufgaben

Grundkurs Mathematik (Baden-Württemberg): Abiturprüfung 1997
Analysis I.1.
Gegeben ist die Funktion f durch f(x) = − 1 x5 + 1 x3 ; x ∈ IR.
30
2
a) Untersuchen Sie die Funktion f auf Symmetrie, gemeinsame Punkte mit den Koordinatenachsen
sowie auf Hoch-, Tief- und Wendepunkte. Zeichnen Sie die Funktion f für -4 ≤ x ≤ 4.
(Längeneinheit l cm )
b) Ein Punkt P (u| v) auf dem Graph der Funktion f mit 0 < u < 15 bestimmt zusammen mit 0 (0|
0) und Q (0| v) ein Dreieck OPQ. Durch Rotation dieses Dreiecks um die y-Achse entsteht ein
Kegel. Für welches u wird das Volumen dieses Kegels maximal?
Geben Sie das maximale Volumen auf zwei Dezimalen gerundet an.
c) Der Graph der Funktion f schließt mit der positiven x-Achse eine Fläche A ein. A wird durch die
Parallele zur y-Achse durch den Hochpunkt H vom Graph der Funktion in zwei Teile geteilt.
Berechnen Sie die Inhalte der beiden Teilflächen.
Eine Gerade g durch H halbiert die Fläche A.
An welcher Stelle schneidet g die x-Achse?
d) Begründen Sie, warum eine Ursprungsgerade mit dem Graph der Funktion nur einen oder drei
oder fünf gemeinsame Punkte haben kann.
Welche Ursprungsgeraden haben mit K genau fünf gemeinsame Punkte?
Analysis I.2.
Gegeben ist die Funktion f durch f(x) =
36x − 48
x3
; x ≠ 0.
a) Untersuchen Sie die Funktion auf Asymptoten, gemeinsame Punkte der der x-Achse, Extremund Wendepunkte. Zeichnen Sie die Funktion für -8 ≤ x ≤ 8. (Längeneinheit 1 cm)
Bestimmen Sie anhand der Zeichnung des Graphen die Anzahl der Lösungen der Gleichung
36x − 48
= c in Abhängigkeit von c.
x
3
b) Der Graph der Funktion, die x-Achse und die Gerade x = z mit z >
4
3
begrenzen eine Fläche mit
dem Inhalt A(z). Berechnen Sie A(z). Untersuchen Sie A(z) für z → ∞.
c) P(u| v) mit u > 43 ist ein Punkt auf dem Graph der Funktion. Der Schnittpunkt N vom Graph der
Funktion mit der x-Achse, der Punkt R (u| 0) und P sind Eckpunkte eines Dreiecks NRP.
Bestimmen Sie u so, dass der Inhalt dieses Dreiecks extremal wird. Ermitteln Sie die Art des
Extremums und seinen Wert.
d) Die Hyperbel y = xa mit a > 0 berührt den Graph der Funktion. Bestimmen Sie a und den
Berührpunkt.
Zeigen Sie: Mit Ausnahme des Berührpunktes verläuft diese Hyperbel für x > 0 stets oberhalb
des Graphen der Funktion.
Analysis I.3.
Gegeben sind die Funktionen f und g durch f(x) = e und g(x) = e ; x ∈ IR. Der Graph von f sei
Kf, der Graph von g sei Kg.
a) Untersuchen Sie sowo hl Kf als auch Kg auf gemeinsame Punkte mit den Koordinatenachsen und
auf Asymptoten.
Berechnen Sie die Koordinaten des Schnittpunktes und den Schnittwinkel von Kf und Kg.
Zeichnen Sie Kf für -1 ≤ x ≤ 2,5 und Kg für -0,5 ≤ x ≤ 3 in ein gemeinsames Koordinatensystem.
(Längeneinheit 2 cm).
b) Die Kurven Kf und Kg schließen mit der y-Achse eine Fläche ein. Rotiert diese Fläche um die x Achse, so entsteht ein Drehkörper. Berechnen Sie das Volumen dieses Drehkörpers.
c) P(u| v) mit u > 0 sei ein Punkt auf der Kurve Kg. Die Parallele zur x - Achse durch P schneidet
die y - Achse in Q. Die Tangente in P an Kg schneidet die y - Achse in R. Für welchen Wert von
x−1
1− x
u wird der Flächeninhalt des Dreiecks QPR extremal? Bestimmen Sie die Art des Extremums
und seinen Wert.
d) Die Temperatur T(t) eines Körpers verändert sich in Abhängigkeit von der Zeit t nach folgendem
Gesetz: T(t) = 50 + 150e-kt ; k > 0; (Zeit t in min; Temperatur T(t) in °C). Zeigen Sie, dass es sich
um einen Abkühlungsvorgang handelt.
Welche Temperaturen kann der Körper für t ≥ 0 annehmen?
Berechnen Sie k auf drei Dezimalen gerundet, wenn sich der Körper in den ersten 35 min auf
62,9°C abgekühlt hat.
Ab welchem Zeitpunkt nimmt für dieses k die Temperatur des Körpers in einer Minute um
weniger als zwei Grad ab?
Analytische Geometrie II. 1.
In einem kartesischen Koordinatensystem sind die Punkte A(5| 1| 0), B(1| 5| 2), C(-1| 1| 6) und
S(6| 3| 7) sowie die Gerade g:
 2  2 
r    
x =  −5  + r  4  ;
 −3   5 
   
r ∈ IR gegeben. Die Ebene E enthält die Punkte A, B
und C.
a) Bestimmen Sie eine Koordinatengleichung von E.
Berechnen Sie die Koordinaten des Schnittpunktes von g und E. Zeigen Sie, dass das Dreieck
ABC gleichschenklig und rechtwinklig ist.
Der Punkt D bildet zusammen mit A, B und C ein Quadrat mit Mittelpunkt M. Bestimmen Sie
die Koordinaten von D und M (Teilergebnis: E: 2x + y + 2z = 11).
b) Zeigen Sie, dass S die Spitze einer senkrechten Pyramide P mit dem Quadrat ABCD als
Grundfläche ist. Zeichnen Sie ein Schrägbild der Pyramide P sowie die Höhe MS (Längeneinheit
1 cm; Verkürzungsfaktor in x-Richtung 12 2 ).
Welchen Winkel schließt die Ebene F mit der Kante AS ein?
c) Berechnen Sie das Volumen der Pyramide P aus Teilaufgabe b. Zu jedem Punkt S* der Geraden
g gibt es eine Pyramide mit der Spitze S* und der Grundfläche ABCD. Zeigen Sie, dass P eine
dieser Pyramiden ist.
Unter diesen Pyramiden gibt es solche, deren Volumen halb so groß ist wie das der Pyramide P.
Bestimmen Sie die Koordinaten der zugehörigen Spitzen.
d) Der Punkt M1 ist von allen fünf Ecken der Pyramide P aus Teilaufgabe b gleich weit entfernt.
Bestimmen Sie die Koordinaten des Punktes M1 .
Wie groß ist der Abstand des Punktes M1 zu den Eckpunkten der Pyramide?
Eine senkrechte quadratische Pyramide hat die Grundkantenlänge a und die Höhe h. Jede dieser
Pyramiden besitzt einen Punkt M*, der von allen Ecken gleich weit entfernt ist.
Welche Beziehung muss zwischen a und h bestehen. damit M* innerhalb der Pyramiden liegt?
Analytische Geometrie II.2.
Vor einem größeren Gebäude befindet sich ein Pavillon, der als gläserne Pyramide mit
quadratischer Grundfläche ausgeführt ist Die Punkte A (4| 2| 0), B (10| -6| 0) und D (12| 8| 0) sind
Ecken der Pyramidengrundfläche; die Maßeinheit ist 1 m. Die Spitze der Pyramide befindet sich in
der Höhe h = 10 m senkrecht über der Mitte der Grundfläche.
a) Berechnen Sie die Koordinaten der vierten Ecke C der Pyramidengrundfläche und der Spitze S
der Pyramide. Zeic hnen Sie ein Schrägbild der Pyramide (1 m entsprechen 0,5 cm;
Verkürzungsfaktor in x - Richtung 12 2 ). Berechnen Sie die Längen der Pyramidenkanten AB
und AS. (Teilergebnis: S(11| 1| 10))
b) Die Punkte A, B und S liegen in der Ebene E1 , die Punkte A, D und S in der Ebene E2 . Geben
Sie jeweils eine Gleichung der Ebene E1 bzw. E2 an. Berechne n Sie den Schnittwinkel der beiden
Ebenen. (Teilergebnis: E1 : 8x + 6y - 5z = 44)
c) Im Innern des Pavillons ist ein Modell der Erdkugel mit dem Durchmesser d = 2 m so
aufgehängt, dass sich der Kugelmittelpunkt senkrecht unter der Pyramidenspitze befindet und
von dieser den Abstand 3 m hat. Geben Sie eine Kugelgleichung an.
Weisen Sie nach, dass die Kugel die Seitenflächen der Pyramide nicht berührt.
Berechnen Sie den Abstand zwischen der Kugeloberfläche und einer Seitenfläche der Pyramide.
Die Kugel soll nun durch eine größere ersetzt werden, welche die Seitenflächen der Pyramide
berührt und deren tiefster Punkt vom Boden den Abstand 4 m hat. Bestimmen Sie den neuen
Radius und den neuen Mittelpunkt.
d) Am Abend wird die Pyramide von außen mit einem punktförmigen Strahler beleuchtet, der sich
im Punkt P (22| 0| 0) befindet. Die Vo rderfront des benachbarten Gebäudes liegt in der yz Ebene. Auf ihr ist dann der Schatten der Pyramide vollständig zu sehen. Berechnen Sie den
Inhalt der Fläche des Schattens der Pyramide auf der Gebäudevorderfront.
Der Strahler befindet sich nun im Punkt P* (a| 0| 0) mit a > 22. Bestimmen Sie die Koordinaten
des Schattens der Pyramidenspitze S in Abhängigkeit von a.
Untersuchen Sie, wohin der Schatten von S wandert, wenn der Strahler auf der x-Achse immer
weiter von der Pyramide entfernt wird. Geben Sie die Koordinaten des Schattens von S für den
Fall an, dass a → ∞ geht.