Physik - Ingenieur-Buch
Werbung
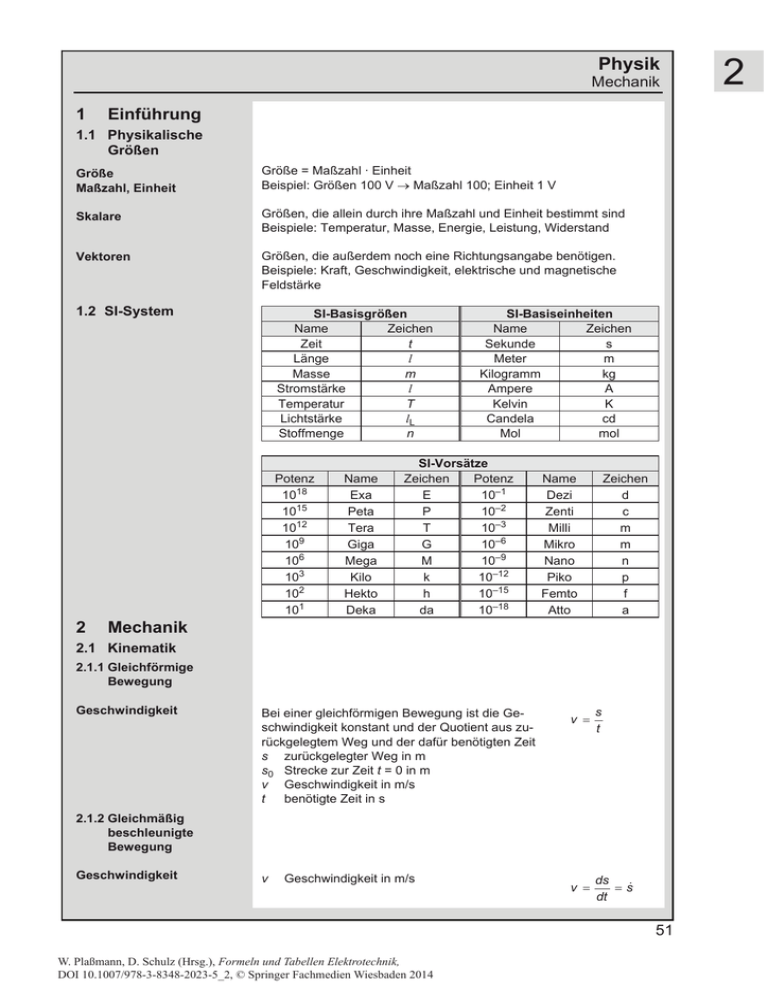
Physik Mechanik 1 Einführung 1.1 Physikalische Größen Größe Maßzahl, Einheit Größe = Maßzahl · Einheit Beispiel: Größen 100 V o Maßzahl 100; Einheit 1 V Skalare Größen, die allein durch ihre Maßzahl und Einheit bestimmt sind Beispiele: Temperatur, Masse, Energie, Leistung, Widerstand Vektoren Größen, die außerdem noch eine Richtungsangabe benötigen. Beispiele: Kraft, Geschwindigkeit, elektrische und magnetische Feldstärke 1.2 SI-System SI-Basisgrößen Name Zeichen Zeit t Länge l Masse m Stromstärke l Temperatur T Lichtstärke lL Stoffmenge n Potenz 1018 1015 1012 109 106 103 102 101 2 Name Exa Peta Tera Giga Mega Kilo Hekto Deka SI-Basiseinheiten Name Zeichen Sekunde s Meter m Kilogramm kg Ampere A Kelvin K Candela cd Mol mol SI-Vorsätze Zeichen Potenz E 10–1 P 10–2 T 10–3 G 10–6 M 10–9 k 10–12 h 10–15 da 10–18 Name Dezi Zenti Milli Mikro Nano Piko Femto Atto Zeichen d c m m n p f a Mechanik 2.1 Kinematik 2.1.1 Gleichförmige Bewegung Geschwindigkeit Bei einer gleichförmigen Bewegung ist die Geschwindigkeit konstant und der Quotient aus zurückgelegtem Weg und der dafür benötigten Zeit s zurückgelegter Weg in m s0 Strecke zur Zeit t = 0 in m v Geschwindigkeit in m/s t benötigte Zeit in s v s t v ds dt 2.1.2 Gleichmäßig beschleunigte Bewegung Geschwindigkeit v Geschwindigkeit in m/s s 51 W. Plaßmann, D. Schulz (Hrsg.), Formeln und Tabellen Elektrotechnik, DOI 10.1007/978-3-8348-2023-5_2, © Springer Fachmedien Wiesbaden 2014 2 2 Physik Mechanik Beschleunigung a Beschleunigung in m/s2 Zurückgelegter Weg s s0 v0 a t Ort in m Strecke zur Zeit t = 0 in m Anfangsgeschwindigkeit in m/s Beschleunigung in m/s2 benötigte Zeit in s Erreichte Geschwindigkeit v v0 a t Geschwindigkeit in m/s Anfangsgeschwindigkeit in m/s Beschleunigung in m/s2 benötigte Zeit in s Fallzeit g h Erdbeschleunigung = 9,81 m/s2 Fallhöhe in m Geschwindigkeit beim Auftreffen a dv dt s s0 v 0t v v 0 at tF 2h g ve Endgeschwindigkeit in m/s ve 2hg Flughöhe hs maximale Flughöhe in m tF Flugzeit in s zum Auftreffen auf dem Boden in s hs Flugzeit ve Endgeschwindigkeit in m/s h0 Anfangshöhe in m v0 Anfangsgeschwindigkeit in m/s tF s v 1 2 at 2 2.1.3 Freier Fall 2.1.4 Senkrechter Wurf Geschwindigkeit beim Auftreffen g Erdbeschleunigung = 9,81 m/s2 h0 v 02 2g v 0 v 02 2h0 g g ve v 02 2h0 g 2.1.5 Schiefer Wurf Flughöhe tF Flugzeit in s v0 Anfangsgeschwindigkeit in m/s Flugzeit h0 Anfangshöhe in m D Startwinkel, gemessen gegen die Horizontale g Flugweite 52 Erdbeschleunigung = 9,81 m/s2 xw Flugweite in m hmax h0 v 02 sin2 D 2g tF v 0 sinD g v 0 sinD 2 2gh0 g xw v 0 tF cos D Physik Mechanik 2.1.6 Kreisbewegung, Rotation Frequenz; Periodendauer Bahngeschwindigkeit; Umfangsgeschwindigkeit Winkelgeschwindigkeit; Kreisfrequenz vu Umfangsgeschwindigkeit in m/s Z M r n f T D f 1 T Winkelgeschwindigkeit oder Kreisfrequenz in 1/s Winkel im Bogenmaß, in rad vu Zr Radius des Kreises in m Drehzahl in 1/min Frequenz in Hz Zeit für eine Umdrehung in s, Periodendauer Winkelbeschleunigung in 1/s2 Z 'M Z 't 2Sf 2.2 Dynamik 2.2.1 Newtonsche Axiome 1. Axiom: Trägheitsgesetz Jeder Körper beharrt im Zustand der Ruhe oder der gleichförmig geradlinigen Bewegung, solange er nicht durch äußere Kräfte gezwungen wird, diesen Zustand zu ändern. 2. Axiom: Aktionsgesetz Die zeitliche Änderung der Bewegungsgröße G (Impuls) ist gleich der resultierenden Kraft F . G F G p 3. Axiom: Wechselwirkungsgesetz actio = reactio Wirkt ein Körper 1 auf einen Körper 2 mit der Kraft F12, so wirkt der Körper 2 auf den Körper 1 mit einer gleich großen, entgegengesetzten Kraft F21. 2.2.2 Kraft G G 'p 't G mv G F12 F21 1N 1 G Einheit Die Kraft F ist ein Vektor mit der Einheit |F| [F] = 1 N (Newton). Kraft F Kraft in N m Masse in kg a Beschleunigung in m/s2 F Rückstellkraft einer Feder FF Rückstellkraft einer Feder in N c Federkonstante in N/m x Auslenkung der Feder in m FF c x Kräfte auf Schiefen Ebenen FH FN m g FN mg cosD D Hangabtriebskraft in N Normalkraft in N Masse in kg Erdbeschleunigung Neigungswinkel der Schiefen Ebene kg m s2 ma 53 2 2 Physik Mechanik Reibungskraft FR Reibungskraft in N FN Normalkraft in N P Reibungszahl FR P FN Zentrifugalkraft FZ Zentrifugalkraft in N m Masse in kg Z Winkelgeschwindigkeit in 1/s r Radius des Kreises in m FZ m Z2 r Gravitationskraft FG Gravitationskraft N J Gravitationskonstante m1 Masse 1 in kg m2 Masse 2 in kg r12 Abstand zwischen den Massen in m Gravitationsgesetz J m1m2 FG 2 r12 J = 6,67259 10 11 Nm2 kg2 2.2.3 Impuls, Drehimpuls Impuls Impulserhaltungssatz Drehimpuls Drehimpulserhaltungssatz p m v 'p 't Impuls in kg m/s Masse in kg Geschwindigkeit in m/s Impulsänderung in kg m/s Zeitdifferenz in s Wirken auf ein System keine äußeren Kräfte, so ist der Gesamtimpuls konstant. p mv F 'p 't G G p1 p2 p3 ... pn ¦i pi const Drehimpuls in kg m2/s Trägheitsmoment in kg m2 Z Winkelgeschwindigkeit in 1/s 'L Drehimpulsänderung in kg m2/s 't Zeitdifferenz in s L JZ M 'L 't Wirken auf ein System keine äußeren Drehmomente, so ist der Gesamtdrehimpuls konstant. L1 L2 L3 ... Ln L J oder const oder const ¦i Li const 2.2.4 Arbeit, Energie Einheit Besitzt ein Körper Energie, so kann er Arbeit verrichten. Arbeit und Energie haben die gleiche Einheit. Es gibt verschiedene Energieformen. 1J >W @ Arbeit, Energie Arbeit = Kraft mal Weg W Energie in J F Kraft in N s Strecke in m W Lageenergie oder potenzielle Energie Wpot m g h Wpot 54 potenzielle Energie in J Masse in kg Erdbeschleunigung Höhenunterschied in m 1Nm 1 1Nm Fs mgh kg m2 s2 1 J (Joule) Physik Mechanik Bewegungsenergie oder kinetische Energie, Translation Bewegungsenergie oder kinetische Energie, Rotation trans Energie in J Wkin m v Masse in kg Geschwindigkeit in m/s rot Wkin Energie in J m2 J Z Trägheitsmoment in kg Winkelgeschwindigkeit in 1/s Elastische Energie einer Feder Welas c x elastische Energie in J Federkonstante in N/m Auslenkung der Feder in m Reibungsenergie WR FN Reibungsenergie in J Normalkraft in N Reibungszahl Strecke in m P s Energieerhaltungssatz 1 m v2 2 trans Wkin In einem abgeschlossenen System ist die Summe aller Energien zu jedem Zeitpunkt konstant. 1 J Z2 2 rot Wkin 1 c x2 2 Welas WR WR P FN s Pmgs W1 W2 W3 ... Wn const 2.2.5 Leistung, Wirkungsgrad J s Einheit >P @ Leistung P W t Leistung in W Arbeit oder Energie in J Zeit in s Leistung bei gradliniger Bewegung P F v Leistung bei Rotation P F d Z P M Wirkungsgrad K Pab Pzu 1 1 W (Watt) 1W 1 J s 1 Nm2 s3 P W t Leistung in W Kraft in N Geschwindigkeit in m/s P Fv Leistung in W Kraft in N Durchmesser des Kreises in m Winkelgeschwindigkeit in 1/s Leistung in W Drehmoment in Nm P F SdZ P MZ K Pab Pzu K K1 K2 K3 ... Gesamtwirkungsgrad abgegebene Leistung in W zugeführte Leistung in W P zu System P ab P v Zusammengesetzter Wirkungsgrad K1,2,3 Einzelwirkungsgrade. Der Gesamtwirkungsgrad ist gleich dem Produkt der Einzelwirkungsgrade. 55 2 2 Physik Mechanik 2.2.6 Trägheitsmoment Definition Das Trägheitsmoment hängt von der J Massenverteilung des Körpers und von der Lage der Massenpunkte zur Drehachse ab. Die Auswertung des Integrals liefert für die speziellen Körper, wenn die Drehachse durch dem Massenmittelpunkt verläuft, folgende Werte: ³ r 2dm >J @ Vol Punktmasse m Masse in kg r Abstand von der Drehachse in m J mr 2 Stab, Achse durch Stabmitte m Masse in kg Länge des Stabes in m l J 1 ml 2 12 Vollzylinder, Drehachse gleich Längsachse m Masse in kg r Radius in m J 1 2 mr 2 Hohlzylinder, Drehachse gleich Längsachse m Masse in kg ra Außenradius in m ri Innenradius in m J 1 m (ra2 ri 2 ) 2 Dünner Ring, Drehachse senkrecht zum Ring m Masse in kg r Radius in m J mr 2 Kugel, Drehachse durch den Mittelpunkt m Masse in kg r Radius in m J 2 2 mr 5 Satz von Steiner Wird dann angewendet, wenn die Drehachse nicht durch den Massenmittelpunkt verläuft, sondern im Abstand a dazu. J Trägheitsmoment Js Trägheitsmoment bezüglich einer Achse durch den Schwerpunkt m Gesamtmasse des rotierenden Körpers in kg a Abstand Drehachse zum Massenmittelpunkt J Js m a 2 2.2.7 Drehmoment Das Drehmoment ist ein Vektor, der senkrecht auf der Ebene steht, die durch den Kraftvektor und den Vektor, der von der Drehachse zum Angriffspunkt der Kraft verläuft, festgelegt ist. Drehmoment M Drehmoment in Nm G r Vektor von der Drehachse zum Angriffspunkt der Kraft in m G F angreifende Kraft in N G G D Winkel zwischen r und F 56 G G G G M r uF M r F sinD 1kg m2 Physik Flüssigkeiten und Gase 3 Flüssigkeiten und Gase 3.1 Druck Druck Hydrostatischer Druck in Flüssigkeiten Druck = Kraft durch Fläche p Druck in Pa F Kraft in N A Fläche in m2 [ p] 1 Pa p p Ugh U g h Schweredruck in Luft, barometrische Höhenformel Druck in Pa Massendichte in kg/m3 Erdbeschleunigung Höhe der Flüssigkeit in m F A p p p0 Druck in Pa Druck am Boden in Pa p U0 Dichte der Luft am Boden g Erdbeschleunigung Höhe über der Erdoberfläche in m nach DIN 5450: p0 = 101325 Pa; U0 = 1,293 kg/m3 p0 e 1 N m2 U gh 0 p0 3.2 Auftrieb Auftriebskraft; Gesamtkraft Auftriebskraft in N FA g UM VM Gewichtskraft in N Fges FG FA gesamte Kraft auf einen Körper in N Erdbeschleunigung Fges g ( UKVK UMVM ) UK Dichte des Körpers in kg/m3 UM Dichte des Mediums in kg/m3 Volumen des Körpers in m3 VK durch den Körper verdrängtes Volumen in m3 Ist der Körper vollständig im Medium eingetaucht, ist VK = VM. FA FG Fges g 3.3 Hydrodynamik Kontinuitätsgleichung U v1, v2 A1, A2 V m Bernoulli-Gleichung pges p pdyn pG U v 'h g Dichte der Flüssigkeit in kg/m3 Geschwindigkeiten an verschiedenen Stellen in m/s Querschnittsflächen an verschiedenen Stellen in m2 Volumenstrom in m3/s Massenstrom in kg/s U v1A1 V m gesamter Druck in Pa pges Betriebsdruck in Pa dynamischer Druck oder Staudruck pges in Pa Schweredruck in Pa Dichte der Flüssigkeit in kg/m3 Geschwindigkeit in m/s h2-h1, Höhenunterschied h1 in m A1 v1 Erdbeschleunigung U U v 2 A2 const vA const p pdyn pG p v 1 U v 2 U g 'h 2 2 A 2 h2 h=0 57 2 2 Physik Thermodynamik Innere Reibung FR A K 'v/'x 4 Reibungskraft in N Fläche in m2 Viskosität in Pa s Geschwindigkeitsgefälle FR K A 'v 'x Thermodynamik 4.1 Temperaturskalen, Ausdehnung von Stoffen T (- 273,15) K - 5 (- F 32)q C 9 Kelvin – Celsius T Celsius – Fahrenheit - Temperatur in qC -F Temperatur in qF Lineare Ausdehnung l0 Ausgangslänge in m 'l Längenänderung in m 'T Temperaturdifferenz in K Dl linearer Ausdehnungskoeffizient in 1/K 'l l0 Volumenausdehnung V0 Ausgangslänge in m 'V Längenänderung in m 'T Temperaturdifferenz in K DV Volumen Ausdehnungskoeffizient in 1/K Dl linearer Ausdehnungskoeffizient in 1/K 'V V0 - Temperatur in K Temperatur in qC D l 'T D V 'T D V | 3 Dl 4.2 Ideale Gase Allgemeine Gleichung idealer Gase p V n R T Druck in Pa Volumen in m3 Anzahl der Mole universelle Gaskonstante Temperatur in K pV nRT Spezielle Gasgleichung p V m Rs T Druck in Pa Volumen in m3 Masse des Gases in kg spezielle Gaskonstante Temperatur in K pV mRs T Universelle Gaskonstante R p0 V0 T0 universelle Gaskonstante = 101325 Pa, Druck bei 0 qC = 22,41383 dm3/mol, Volumen bei 0 qC = 273,15 K, Temperatur bei 0 qC in K p0 = 101325 Pa, Druck bei 0 qC Dichte des Gases bei 0 qC in kg/m3 = 273,15 K, Temperatur bei 0 qC in K Spezielle Gaskonstante U0 T0 Volumen Ausdehnungskoeffizient 58 DV Volumen Ausdehnungskoeffizient in 1/K R p0V0 T0 R 8,31441 J mol K p0 Rs U0T0 Dv 1 273,15K Physik Harmonische Schwingungen Mittlere kinetische Energie der Gasmoleküle Wärmeenergie Wkin k T kinetische Energie in J Boltzmann-Konstante Temperatur in K 3 kT 2 Wkin k 1,38066 1023 'WQ C m c 'T Änderung der Wärmeenergie in J Wärmekapazität in J/K Masse in kg spezifische Wärmekapazität in J/(kg K) Temperaturänderung in K 'WQ m c 'T 'WQ C 'T 'WQ 't Änderung der Wärmeenergie in J Zeitdifferenz in s Wärmeleitfähigkeit Fläche in m2 Temperaturdifferenz in K Materialstärke in m 'WQ 't O A J K 4.3 Wärmeleitung, Wärmestrahlung Wärmeleitung Wärmestrahlung O A 'T 'x S A H V T1,2 5 Leistung in W Fläche in m2 Emissionskoeffizient (H < 1) Stefan-Boltzmann-Konstante Temperaturen in K 'T 'x W [O ] 1 K m S A H V (T24 T14 ) V 5,67 10 8 f 1 Z T W m2K 4 Harmonische Schwingungen 5.1 Ungedämpfte Schwingungen Frequenz; Kreisfrequenz Harmonische Schwingung f T Frequenz in Hz (Hertz) Periodendauer oder Schwingungszeit in s Kreisfrequenz y ŷ M Momentanwert oder Augenblickswert Amplitude oder Spitzenwert Kreisfrequenz in 1/s Zeit in s Phasenverschiebung in rad T l g m c L C Periodendauer oder Schwingungszeit in s Länge des Fadenpendels in m Erdbeschleunigung Masse in kg Federkonstante in N/m Induktivität einer Spule in H Kapazität eines Kondensators in F Z Z0 t Fadenpendel mit kleiner Amplitude; Federpendel; elektrischer Schwingkreis y (t ) 2Sf 2S T yˆ sin (Z 0 t M ) T 2S l g T 2S m c T 2 S LC 59 2 2 Physik Harmonische Schwingungen 5.2 Gedämpfte Schwingungen Harmonische Schwingung Gütefaktor Zeitkonstante Kreisfrequenz y ŷ t Momentanwert oder Augenblickswert Amplitude oder Spitzenwert Abklingkoeffizient in 1/s Kreisfrequenz in 1/s Zeit in s Q Gütefaktor G Z Z0 Kreisfrequenz, ungedämpft, in 1/s G Abklingkoeffizient in 1/s W G Zeitkonstante in s Abklingkoeffizient in 1/s Z Kreisfrequenz, gedämpft, 1/s Z0 Kreisfrequenz, ungedämpft, in 1/s G Abklingkoeffizient in 1/s y (t ) yˆ e G t sin(Z t M ) Z0 Q 2G W 1 G Z Z02 G 2 5.3 Erzwungene Schwingungen, Resonanz Momentanwert der erzwungenen Schwingung y ŷ : M t Amplitude als Funktion der Erregerfrequenz : Phasenverschiebung zwischen System und Erreger yˆ sin( : t M ) F(t) angreifende Kraft in N F (t ) Fˆ cos(: t ) : Kreisfrequenz des Erregers in 1/s m Masse des schwingenden Systems in kg Fˆ / m yˆ Z0 Eigenkreisfrequenz des ungedämpften (Z02 :2 )2 (2G :)2 Systems in 1/s G Abklingkoeffizient in 1/s M Z0 G : 60 Momentanwert oder Augenblickswert y (t ) Amplitude oder Spitzenwert Kreisfrequenz des Erregers in 1/s Phasenwinkel zwischen System und Kraft Zeit in s Phasenwinkel zwischen schwingendem System und angreifender Kraft Eigenkreisfrequenz des ungedämpften Systems in 1/s Abklingkoeffizient in 1/s Kreisfrequenz des Erregers in 1/s tan M 2G Z0 (Z02 :2 )