Prozentrechnung
Werbung
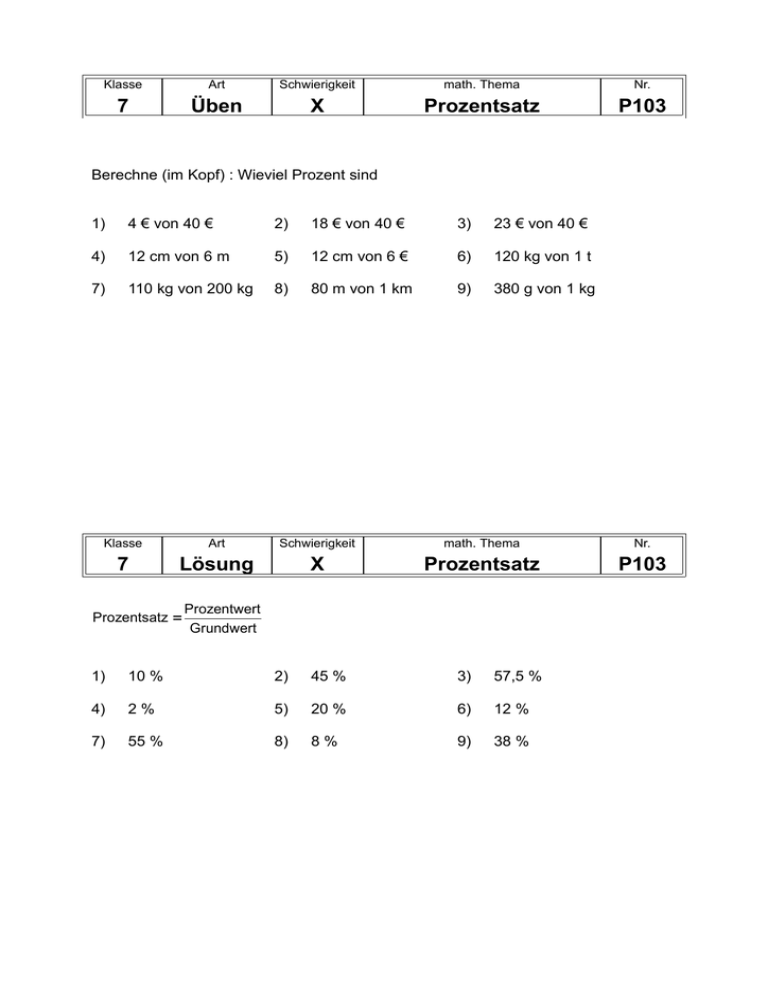
Klasse Art Schwierigkeit math. Thema Nr. 7 Üben X Prozentsatz P103 Berechne (im Kopf) : Wieviel Prozent sind 1) 4 € von 40 € 2) 18 € von 40 € 3) 23 € von 40 € 4) 12 cm von 6 m 5) 12 cm von 6 € 6) 120 kg von 1 t 7) 110 kg von 200 kg 8) 80 m von 1 km 9) 380 g von 1 kg Klasse Art Schwierigkeit math. Thema Nr. 7 Lösung X Prozentsatz P103 Prozentsatz Prozentwert Grundwert 1) 10 % 2) 45 % 3) 57,5 % 4) 2% 5) 20 % 6) 12 % 7) 55 % 8) 8% 9) 38 % Klasse Art Schwierigkeit math. Thema Nr. 7 Üben X Prozentsatz P104 Das Modehaus Kleidsam bietet eine Lederjacke im Sommerschlussverkauf zu 142,50 € an. Ihr regulärer Preis wäre 190 €. Wie hoch ist der Preisnachlass in Prozent? Klasse Art Schwierigkeit math. Thema Nr. 6 Lösung X Prozentsatz P104 Prozentsatz Prozentwert Grundwert Prozentsatz = 47 , 50 € 1 = = 25 % 190 € 4 Klasse Art Schwierigkeit math. Thema Nr. 7 Üben X Prozentsatz u. Prozentwert P201 Verwandle folgende Bruchteile durch schriftliches Dividieren in Dezimalbrüche und gib die zugehörigen Prozentsätze auf eine Dezimale gerundet an: 1) 5 12 2) 3 7 3) 7 9 4) 11 18 5) 23 30 6) 9 19 7) 13 17 8) 10 11 Klasse Art Schwierigkeit math. Thema Nr. 7 Lösung X Prozentsatz u. Prozentwert P201 1) 41,7 % 2) 42,9 % 3) 77,8 % 4) 61,1 % 5) 76,7 % 6) 47,4 % 7) 76,5 % 8) 90,9 % Klasse Art Schwierigkeit math. Thema Nr. 7 Üben X Prozentsatz u. Prozentwert P202 Berechne folgende Prozentwerte: 1) 10 % von 48 € 2) 25 % von 120 € 3) 2 % von 80 € 4) 18 % von 75 kg 5) 120 % von 250 m 6) 17 % von 70 kg 7) 33 8) 37 1 % von 160 € 2 9) 98 % von 250 kg 1 % von 90 cm 3 Klasse Art Schwierigkeit math. Thema Nr. 7 Lösung X Prozentsatz u. Prozentwert P202 18 18 3 75kg kg 13,5kg 100 4 Lösungsweg: 4) 18 % von 75 kg = 1) 4,80 € 2) 30 € 3) 1,60 € 4) 13,5 kg 5) 300 m 6) 11,9 kg 7) 30 cm 8) 60 € 9) 245 kg 777 Klasse Art Schwierigkeit math. Thema Nr. 7 Üben XX Prozentsatz u. Prozentwert P204 Ein Sportartikelgeschäft verkauft seine Waren wegen eines Umbaus um 18 % billiger. Wieviel kostet dann ein Skianorak, der vorher a) 114 € b) 160 € c) 179,50 € gekostet hat? Klasse Art Schwierigkeit math. Thema Nr. 7 Lösung XX Prozentsatz u. Prozentwert P204 a) 18 % von 114 € = 18 114 € = 20,52 € 100 Der neue Preis ist also 114 € - 20,52 € = 93,48 €. b) Der neue Preis ist 131,20 €. c) Der neue Preis beträgt 147,19 €. Klasse Art Schwierigkeit math. Thema Nr. 7 Üben XXX Prozentsatz u. Prozentwert P205 Herr Meier kauft eine neue Gefriertruhe für 544 €. Er erhält wegen eines Lackschadens einen Rabatt von 15 %. Bei Bezahlung der Rechnung innerhalb von 14 Tagen darf er zusätzlich noch 2 % Skonto abziehen. a) Wieviel muss er nach Abzug des Rabatts bezahlen? b) Wieviel muss er nach Abzug von Rabatt und Skonto bezahlen? (Beachte: Die 2 % Skonto beziehen sich auf den Rechnungsbetrag von a) . ) Klasse Art Schwierigkeit math. Thema Nr. 7 Lösung XXX Prozentsatz u. Prozentwert P205 a) 15 % von 544 € = 15 544 € = 81,60 € 100 Der Preis nach Abzug des Rabatts ist also 544 € - 81,60 € = 462,40 € b) 2 % von 462,40 € = 2 462,40 € = 9,248 € 9,25 € 100 Der Preis nach Abzug von Rabatt und Skonto beträgt 453,15 € Klasse Art Schwierigkeit math. Thema Nr. 7 Üben XXX Grundwertberechnung P304 Berechne den jeweiligen Grundwert: 1) 25 % von x sind 2,60 € 2) 8 % von x sind 9,6 kg 3) 4 % von x sind 24 € 4) 3 5) 17,5 % von x sind 105 m 6) 7 % von x sind 18 € 1 % von x sind 75 € 3 Klasse Art Schwierigkeit math. Thema Nr. 7 Lösung X Grundwertberechnung P302 Lösungsweg: Grundwert 1) Grundwert = Prozentwert Prozentsatz 2,60 € 25 = 10,40 € 100 2) Grundwert = 9,6kg 8 = 120 kg 100 24dm 4 3) Grundwert = = 600 € 100 75 € 1 4) Grundwert = 3 = 2250 € 3 100 105m 5) Grundwert = 17,5 = 600 m 100 18 € 6) Grundwert = 7 257,14 € 100 Klasse Art Schwierigkeit math. Thema Nr. 7 Üben XX Grundwertberechnung P303 Auf Grund einer Wohnungsrenovierung muss Herr Altmann ab 1.1. um 66,50 € mehr Miete bezahlen, das sind 7 % mehr als bisher. Berechne seine alte und seine neue Miete. Klasse Art Schwierigkeit math. Thema Nr. 7 Lösung XX Grundwertberechnung P303 Lösungsweg: Grundwert Prozentwert Prozentsatz 66,50 € alte Miete = 7 = 950 € 100 neue Miete = 950 € + 66,50 € = 1016,50 € Klasse Art Schwierigkeit math. Thema Nr. 7 Üben XXX Grundwertberechnung P304 Der Preis einer Skimarke stieg im Vergleich zum Vorjahr um 8 % an. Im Winterschlussverkauf in diesem Jahr wurde sie jedoch wieder um 12 % billiger angeboten und kostete nun 427,68 €. Wie teuer waren die Ski im Vorjahr und in diesem Jahr vor dem Winterschlussverkauf? Klasse Art Schwierigkeit math. Thema Nr. 7 Lösung XXX Grundwertberechnung P304 Der Preis im Sommerschlussverkauf ist 88 % des Preises der neuen Saison. 427,68 € Preis (dieses Jahr) = 88 = 486 €. 100 Der Preis in diesem Jahr beträgt 108 % des Vorjahrespreises. Preis (Vorjahr) = 486 € 108 = 450 € 100 Klasse Art Schwierigkeit math. Thema Nr. 7 Üben XX Prozentrechnen: Vermischtes P401 Ein Kühlschrank, der bisher 640 € gekostet hatte, wurde um 6 % teurer. Da der Absatz danach jedoch stark gesunken war, will die Firma die Preiserhöhung wieder rückgängig machen. a) Zu welchem Preis gelangt sie, wenn sie den neuen Preis um 6 % herabsetzt? b) Der neue Preis wird nun auf den alten Preis von 640 € wieder heruntergesetzt. Wieviel Prozent Preisnachlass gibt die Firma? Klasse Art Schwierigkeit math. Thema Nr. 7 Lösung XX Prozentrechnen: Vermischtes P401 Neuer Preis (nach 6 % Erhöhung) : 6 % von 640 € = 38,40 € Der neue Preis beträgt 678,40 € a) Preisnachlass von 6 %: 6 % von 678,40 € 40,70 € Der reduzierte Preis beträgt 637,70 € b) Preisnachlass um 38,40 € 38,40 € bezogen auf 678,40 € sind 38, 40 = 0,0566 5,7 % 678,40 Klasse Art Schwierigkeit math. Thema Nr. 7 Üben XX Prozentrechnen: Vermischtes P402 Eine Rechnung wurde nach Abzug von 12 % Rabatt mit 404,80 € beglichen. a) Wie hoch war der Rabatt in € b) Wie hoch war der ursprüngliche Rechnungsbetrag? Klasse Art Schwierigkeit math. Thema Nr. 7 Lösung XX Prozentrechnen: Vermischtes P402 88 % des ursprünglichen Preises sind 404,80 €. 404,80 88 Der Grundwert ist: = 460 €. (ursprünglicher Rechnungsbetrag) 100 Der Rabatt betrug also 460 € - 404,80 € = 55,20 €. Klasse Art Schwierigkeit math. Thema Nr. 7 Üben XX Prozentrechnen: Vermischtes P403 Ein Elektroherd der Marke „Kochgut“ kostet beim Einzelhändler 1080 €. Der Großhändler, der dem Einzelhändler die Ware liefert, hat bereits eine Gewinnspanne von 20 %. Familie Meier kauft den Herd beim befreundeten Einzelhändler und erhält von diesem einen Preisnachlass von 25 % . Familie Huber ist mit dem Großhändler befreundet und erhält von ihm den Herd um 5 % günstiger. Wieviel müssen beide Familien jeweils für den Herd bezahlen? Klasse Art Schwierigkeit math. Thema Nr. 7 Lösung XX Prozentrechnen: Vermischtes P403 Preis beim Großhändler: 120 % ≙ 1080 € 100 % ≙ 1080€ : 1,2 = 900 € Preisnachlass Familie Meier: 25 % von 1080 € sind 270 €. Meiers zahlen also 810 € Preisnachlass Familie Huber: 5 % von 900 € sind 45 €. Hubers zahlen also 855 €. Klasse Art Schwierigkeit math. Thema Nr. 7 Üben XX Prozentrechnen: Vermischtes P404 Eine Autofirma erhöht die Preise für ihre Marke „Rasant“ um 3,5 % . Dabei erhöht sich der Preis für dieses Fabrikat um 665 €. Wie hoch war der Preis vor der Preiserhöhung? Wie hoch ist der Preis nun? Klasse Art Schwierigkeit math. Thema Nr. 7 Lösung XX Prozentrechnen: Vermischtes P404 3,5 % ≙ 665 € 100 % ≙ 665€ : 0,035 = 19000 € Der Preis vor der Preiserhöhung betrug 19000 €, heute beträgt er 19665 €