Versuch 1

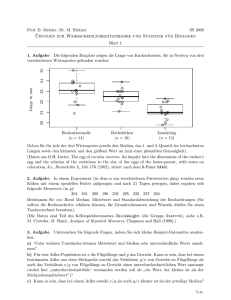
VERSUCH 1: STATISTIK
UND
DATENVERARBEITUNG
THEORETISCHE GRUNDLAGEN
In der Biophysik versuchen wir biologische Vorgänge mit physikalischen Methoden zu
untersuchen und zu verstehen. Wir setzen dabei voraus, dass biologische Größen quantitativ
gemessen und mit mathematischen Modellen beschrieben werden können. Wegen der Komplexität
biologischer Systeme und der inhärenten Messfehler unserer Methoden werden dabei oft sehr
viele Messungen durchgeführt und entsprechend viele Daten fallen an. Um diese
(fehlerbehafteten) Daten zu analysieren und zueinander in Beziehung zu setzen, verwenden
wir Methoden der statistischen Datenanalyse. Wegen der Vielzahl der zu verarbeitenden Werte
werden dazu heute vor allem elektronische Datenverarbeitungsanlagen (aka Computer) mit
geeigneter Software verwendet.
STATISTIK
"Ich glaube nur die Statistik, die ich selbst gefälscht habe."
Diese fälschlich Winston Churchill zugeschriebene Aussage wird oft als Argument gegen die
Statistik zitiert, unterstellt aber, dass Churchill bewusst falsche Daten und/oder falsche
Methoden zuließ. Unredlichkeit und Voreingenommenheit beim Umgang mit Daten können
nur die betreffenden Anwender, nicht aber die naturwissenschaftliche Methode abqualifizieren.
Statistik dient dazu, Daten die durch zufällige Ereignisse beeinflusst werden zu beschreiben
bzw. aus solchen Daten allgemeine Aussagen abzuleiten oder vorherzusagen. Dies betrifft fast
alle Daten, die aus Messungen hervorgegangen sind, da diese unvermeidlich mit einem
(zufälligen) Messfehler behaftet sind. Gemessene Daten sind also nicht exakt, sondern immer
mehr oder weniger genaue Schätzwerte und die Statistik hilft uns bei der Beurteilung der
Genauigkeit dieser Werte und der daraus abgeleiteten Aussagen. (Hier sei z.B. die Frage der
"signifikanten Stellen" eines Messwertes aufgeworfen).
Statistik verwendet zwar mathematische Verfahren wird aber nicht als eigentlicher Zweig der
Mathematik aufgefasst. Sie verwendet vielmehr standardisierte Rechenvorschriften um
statistische Maßzahlen zu gewinnen, die unsere Daten und ggf. ihre Genauigkeit beschreiben.
Die Gewinnung dieser Maßzahlen aus den Rohdaten ist (bei gewissenhafter Anwendung der
Regeln s. o.) reproduzierbar und erlaubt uns daher eine objektivere Beurteilung unserer
Ergebnisse. Neben der Unzulänglichkeit des Beobachters sowie der Instrumente kommen in der
Biologie noch die natürlichen Schwankungen der lebenden Systeme hinzu, die eine eindeutige
Aussage erschweren. Eine mathematisch-statistische Auswertung der Beobachtungen lässt sich
daher kaum vermeiden.
BESCHREIBENDE STATISTIK
Die beschreibende Statistik liefert Informationen in Form von empirischer Zahlen (Statistiken Umfrageergebnisse) über Populationen bei denen die untersuchten Größen zufällig schwanken.
Mit der mathematischen Statistik analysiert man also Massenerscheinungen. Dabei zeigt sich
9
VERSUCH 1: STATISTIK UND DATENVERARBEITUNG
oft, dass die Massenerscheinungen gewisse Gesetzmäßigkeiten aufweisen, die sich für
Einzelerscheinungen nicht formulieren lassen, da sie dort nur als zufällige Unregelmäßigkeit
auftreten. Werden z.B. 100 Bohnen einer bestimmten Sorte einzeln gewogen, so streuen die
einzelnen Werte zufällig und sind somit nicht vorhersagbar. Das mittlere Gewicht und die
Streuung der Werte jedoch sind auch nach dem Auszählen einer zweiten Stichprobe nahezu
identisch. Diese charakteristischen Werte erlauben somit eine Aussage über die Grundgesamtheit
aller Bohnen dieser Sorte.
In der Wahrscheinlichkeitsrechnung wird der Mittelwert als Erwartungswert interpretiert. In der
Bundesrepublik sterben jährlich 100 Personen aufgrund eines technischen Defekts an einem
elektrischen Haushaltsgerät. Glaubhaft, da ein eng definiertes, singuläres Schadensereignis. Auf
der Welt sterben jährlich über zwei Millionen Menschen an den Folgen ihres Nikotinkonsums.
Dies wird nicht geglaubt, da es sich um ein Multikomponenten Ereignis handelt, von dem jeder
eine Ausnahme kennt.
Die biologische Statistik besteht in erster Linie in einer kritischen Bewertung von
Stichprobenergebnissen. Messungen biologischer Parameter schwanken nicht um einen wahren
Wert, wie etwa eine physikalische Größe im unbelebten System, sondern sie haben eine
beträchtliche Streuung, die durch die biologische Variabilität bedingt ist.
Das Ziel ist, allgemeine Aussagen über spezielle Merkmale gleicher Individuen zu machen. Die
Gesamtheit aller Individuen des zu untersuchenden Materials stellt die Grundgesamtheit dar. Da
es meist nicht möglich ist, alle Individuen zu untersuchen, werden Stichproben durchgeführt. Die
Auswahl dieser Stichproben muss zufällig sein.
TABELLARISCHE
UND GRAPHISCHE
DARSTELLUNG
100
100
80
80
60
60
Häufigkeit N
Häufigkeit N
Üblicherweise werden die n Beobachtungsereignisse (Massen einzelner Bohnen) der Reihe nach
aufgelistet (Urliste). Aus dieser Stichprobe vom Umfang n kann man Schlüsse auf die zugehörige
Grundgesamtheit ziehen. Wären gleichzeitig mehrere Merkmale gemessen worden, z.B. Masse
und Größe, so hätte man eine Stichprobe erhalten, die aus n Zahlenpaaren besteht.
40
20
40
20
0
0
-5
-4
-3
-2
-1
0
1
Klassenmitten
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
3
4
5
Klassenmitten
Abb. 1: Häufigkeitsverteilung einer Gaußschen Normalverteilung. oben: Stabdiagramm. unten:
Balkendiagramm mit Kurvenzug der theoretischen Funktionsgleichung.
Bei kleinen Stichproben hilft es schon, wenn man die Werte der Größe nach ordnet, um einen
10
PHYSIKALISCH-TECHNISCHE METHODEN IN DER BIOLOGIE
Überblick zu bekommen. Besser ist es, zahlenmäßig gleiche Werte zusammenzufassen und sie
graphisch darzustellen. Dabei wird die Anzahl ai über dem Messwert xi aufgetragen. Die Anzahl ai
heißt die absolute Häufigkeit des betreffenden Wertes in der Stichprobe. Dividiert man die
absolute Häufigkeit durch den Stichprobenumfang n, so erhält man die relative Häufigkeit. Die
relative Häufigkeit ist somit immer eine Zahl zwischen 0 und 1. Die Auftragung kann als Punkt-,
Stab- oder Balkendiagramm (Abb. 1) erfolgen. Eine direkte Verbindung der Punkte untereinander
ergibt ein Häufigkeitspolygon (Abb. 1, unten). Diese Graphiken stellen Häufigkeitsverteilungen
oder Histogramme der Stichprobe dar.
KLASSENBILDUNG
Kommen in einer Stichprobe sehr viele zahlenmäßig verschiedene Werte vor, so ist die Tabelle
oder die Zeichnung der Häufigkeitsverteilung meist noch recht unübersichtlich. Man kann in
diesem Fall die Stichprobe weiter vereinfachen, und zwar durch die sog. Gruppierung oder
Klassenbildung im Gegensatz zu den oben genannten nicht gruppierten Werten.
Dabei geht man von dem Intervall aus, in dem alle Stichprobenwerte liegen. Dieses unterteilt
man in Teilintervalle (Abb. 1, oben), die als Klassenintervalle bezeichnet werden. Die Mitten dieser
Intervalle heißen Klassenmitten (Abb. 1, unten). Alle Stichprobenwerte in einem solchen Intervall
bilden zusammen jeweils eine Klasse von Werten. Die ursprünglichen Stichprobenwerte treten
nicht mehr einzeln in Erscheinung. Man nimmt an, dass alle Werte einer Klasse in der
zugehörigen Klassenmitte liegen (Abb. 1, oben). Je weniger Klassen man bildet, desto mehr
Information, die in den ursprünglichen Stichprobenwerten steckt, geht aber verloren. Man sollte
so klassifizieren, dass nur unwesentliche Einzelheiten ausgeschieden werden. In der Praxis wählt
man meist 10 - 20 Klassen und mehr als 20 höchstens bei sehr umfangreichen Stichproben.
Unnötige Komplikationen bei späteren Rechnungen lassen sich vermeiden, wenn man die
folgenden Regeln beachtet:
•
Die Klassenintervalle wählt man gleich lang.
•
Die Klassenmitten sollen möglichst einfachen Zahlen, d.h. Zahlen mit möglichst wenigen
Ziffern, entsprechen.
•
Ein Wert, der auf einen Intervallendpunkt fällt, wird je zur Hälfte in jedem der beiden
angrenzenden Klassenintervalle mitgezählt.
Oftmals kann man die genannten Endpunkte ohne Mühe so wählen, dass sie nicht mit
Stichprobenwerten zusammenfallen. Durch die beschränkten Messgenauigkeiten von
Messgeräten ergeben sich die besten Klassengrenzen oft von selbst, da das Messgerät selbst die
Klasseneinteilung vorgibt.
SUMMENHÄUFIGKEITSFUNKTION
EINER
STICHPROBE
Die Häufigkeitsverteilung einer Stichprobe gibt die Häufigkeiten an, mit der die einzelnen
Zahlenwerte in der Stichprobe vorkommen (Abb. 1, unten). Wenn es 30 Bohnen mit dem Gewicht
3,2 g gibt, man jedoch wissen möchte, wie viele Bohnen 3,2 g oder weniger wiegen, so erhält man
die Antwort durch aufsummieren der einzelnen Häufigkeiten bis x = 3,2 g. Man erhält auf diese
Weise die Summenhäufigkeitsfunktion oder Verteilungsfunktion einer Stichprobe. Die
11
VERSUCH 1: STATISTIK UND DATENVERARBEITUNG
Summenhäufigkeitsfunktion stellt das Integral der Häufigkeitsfunktion dar (Abb. 2). Aus
unstetigen
Häufigkeitsfunktionen
erhält
man
Treppenfunktionen,
aus
stetigen
Häufigkeitsverteilungen Sigmoide. Jede der beiden genannten Funktionen bestimmt die
Stichprobe in allen Einzelheiten. Die Summenhäufigkeitsfunktion (Abb. 2) ist weniger
anschaulich als die Häufigkeitsfunktion (Abb. 1,unten).
Summenhäufigkeit / Klasse
1000
800
600
400
200
0
-4
-3
-2
-1
0
1
2
3
4
Messgrösse x
Abb. 2: Summenhäufigkeit (Treppenfunktion und
Sigmoide) der Häufigkeitsverteilung aus Abb. 1,
(unten).
MITTELWERT, VARIANZ, STANDARDABWEICHUNG, STANDARDFEHLER
Neben der Häufigkeits- bzw. Summenhäufigkeitsfunktion kann man eine Grundgesamtheit oder
eine Stichprobe auch durch Maßzahlen charakterisieren. Die beiden in der Praxis wichtigsten
Maßzahlen sind der Mittelwert, der die durchschnittliche Größe der Grundgesamtheit N oder der
Stichprobe n kennzeichnet, und eine Angabe über die Streuung der Werte. Im Weiteren wird die
Annahme gemacht, dass die Messwerte eine Normalverteilung nach Gauß ergeben (s. u.). Eine
genügend große Stichprobe wird vorausgesetzt.
Der arithmetische Mittelwert ist definiert als:
x1 + x 2 + K x n
n
n
1
= ∑ xi
n i= 1
x=
µ= Mittelwert der Grundgesamtheit,
x = Mittelwert der Stichprobe
Dieser allein reicht jedoch nicht aus, um z. B. eine Stichprobe zu beschreiben, wie folgendes
Beispiel zeigt:
Stichprobe 1:
Stichprobe 2:
1; 2; 4; 5
2,7; 3,0; 3,1; 3,2
x=3
x=3
Beide Stichproben haben den Mittelwert x = 3. Sie unterscheiden sich aber trotzdem
wesentlich voneinander, denn die Werte der ersten Stichprobe liegen viel weiter auseinander
(und auch weiter vom Mittelwert entfernt) als die Werte der zweiten Stichprobe. Um diesen
Unterschied zu erfassen, braucht man noch eine weitere Maßzahl. Geeignet ist hierzu offenbar
12
PHYSIKALISCH-TECHNISCHE METHODEN IN DER BIOLOGIE
eine Zahl, die die Abweichung der Stichprobenwerte vom Mittelwert misst. Man könnte die
Spannweite der Stichprobe, d.h. die Differenz zwischen dem größten (Maximum) und kleinsten
(Minimum) Stichprobenwert ermitteln (Abb. 1, oben: Minimum = 0, Maximum = 100). Es wird
jedoch gefordert, dass ähnlich wie beim Mittelwert jeder Einzelwert in gewisser Weise
mitberücksichtigt wird. Die wohl am nächsten liegende Möglichkeit, die Summe der
Einzelabweichungen xi − x scheidet allerdings aus, da die Summe aus negativen und positiven
Gliedern besteht und diese somit immer Null ist. Dies könnte vermieden werden, wenn man die
Absolutbeträge der Einzelabweichungen bilden würde. Aus mathematischen Ableitungen hat
sich jedoch die Bildung der Quadrate der Einzelabweichungen als günstiger erwiesen. Diese
werden auch als die kleinsten Gaußschen Fehlerquadrate (engl. least squares) bezeichnet. Die
Maßzahl, die man auf diesem Weg erhält heißt Varianz oder Streuung (engl. variance). Sie
berechnet sich für die Grundgesamtheit nach
σ
2
=
1 n
∑ ( xi − µ
n i= 1
)
2
und für die Stichprobe nach
s2 =
1 n
2
( xi − x )
∑
n − 1 i= 1
Aus der Wahrscheinlichkeitstheorie lässt sich die unterschiedliche Berechnung der Varianz für
Grundgesamtheit und Stichprobe ableiten. Man muss im Allgemeinen bei der Berechnung nur
wissen, ob es sich um eine Grundgesamtheit oder eine Stichprobe handelt. (n - 1) bezeichnet man
als die Anzahl der Freiheitsgrade, sie ergeben sich aus der Anzahl unabhängiger Einzelwerte. Die
nichtnegative Quadratwurzel der Varianz heißt Standardabweichung (engl. standard deviation,
S.D.)
σ =
σ
s=
s2 =
2
=
1 n
∑ ( xi − µ
n i= 1
)
2
1 n
∑ ( xi − x )
n − 1 i= 1
Bei Taschenrechnern mit statistischen Programmen muss der Unterschied bei der
Standardabweichung zwischen Grundgesamtheit und Stichprobe durch Auswahl der
entsprechenden Funktionstaste beachtet werden. Die Größen Varianz und Standardabweichung
sind mit demselben Formelbuchstaben belegt, da beide in der Praxis gleichwertig verwendet
werden. Die Varianz hat den Vorteil, dass man sich nicht mit Quadratwurzeln herumärgern
muss. Die Standardabweichung hat den Vorteil, dass sie dieselbe Dimension der Größeneinheit
(z.B. cm oder kg) wie der Mittelwert besitzt.
Für die obigen Beispiele ergeben sich somit:
Stichprobe 1:
Stichprobe 2:
x=3
x=3
s2 = 3,3
s2 = 0,05
s = 1,8
s = 0,22
13
VERSUCH 1: STATISTIK UND DATENVERARBEITUNG
Die Streuung der zweiten Stichprobe ist also wesentlich kleiner. Durch Angabe von Mittelwert
und Varianz bzw. Standardabweichung sind Stichproben meist ausreichend beschrieben.
Die Berechnung der Standardabweichung (bzw. Varianz) nach den Definitionsformeln ist
ungünstig. Durch die Differenzbildung ( x− x ) von den relativ großen Zahlen entstehen sehr
kleine Differenzen, die dann auch noch quadriert werden müssen. Durch Rundungsfehler
entstehen Genauigkeitsverluste, die beim elektronischen Rechnen nicht einmal bemerkt werden.
Es gibt deshalb Berechnungsformeln für die Praxis. Bei ihnen werden die Differenzbildungen
vermieden. Für die Standardabweichung einer Stichprobe ergibt sich somit
s=
2
1  n 2 1 n  
 ∑ xi −  ∑ xi  
n − 1  i = 1
n  i = 1  
Eine ebenfalls verwendete Formel ist:
1  n 2

xi − nx 2 
∑

n − 1  i= 1

s=
Bei der Bestimmung von Stichproben möchte man gerne wissen, mit welcher Wahrscheinlichkeit
sich die bei einer Stichprobe gefundenen Größen auf die Grundgesamtheit ausweiten lassen. Im
Beispiel der Bohnen möchte man also eine Aussage über alle Bohnen einer Sorte machen. Die für
eine Stichprobe ermittelten Werte (Mittelwert, Varianz, Standardabweichung) sind also nur
Schätzwerte für die Grundgesamtheit. Man möchte z.B. wissen, wie weit der
Stichprobenmittelwert x vom Mittelwert der Grundgesamtheit µ abweicht. Diese Abweichung
bezeichnet man als Standardfehler (= Fehler des Mittelwertes = Standardabweichung des
Mittelwertes; engl. standard error of the mean, S.E.M.). Wenn keine extremen Abweichungen der
Stichprobenwerte xi von der Normalverteilung um den Stichprobenmittelwert x vorliegen,
darf man annehmen, dass sich auch die Mittelwerte annähernd gleich großer Stichproben
gleichmäßig um den Grundgesamtheitsmittelwert µ verteilen. Die Abweichung kann durch den
Standardfehler abgeschätzt werden. Er berechnet sich aus der Standardabweichung s.
s
=
n
s
n
∑ (x
−x
sx =
n
=
i= 1
i
)
2
n ( n − 1)
Das zusätzliche n in der Formel für den Standardfehler s (im Gegensatz zu Varianz und
Standardabweichung) liefert eine Angabe über die Größe der Stichprobe. Je größer eine
Stichprobe ist, desto genauer wird die Schätzung für die Grundgesamtheit. Der Standardfehler
verkleinert sich dabei (n steht im Nenner), geht somit gegen µ; (Die Genauigkeit ist dem
Geduldsfaden des Experimentators direkt proportional). Der Standardfehler wird oft zusammen
mit dem Stichprobenmittelwert zur Charakterisierung einer Stichprobe bezüglich der
Grundgesamtheit angegeben:
x ± sx z.B. 5 ±0,6 g
14
PHYSIKALISCH-TECHNISCHE METHODEN IN DER BIOLOGIE
GEWICHTETER MITTELWERT, ZENTRALWERT, HÄUFIGSTER WERT
Teilt man die Messwerte in k Klassen ein (Gruppierung, Abb. 1, unten), so lässt sich der
arithmetische Mittelwert auch als gewichteter Mittelwert x gew. (gewogenes Mittel) berechnen.
Dazu wird jede mittlere Klassengröße xi mit ihrer Klassenhäufigkeit ai multipliziert.
x gew . =
=
a1 x1 + a2 x 2 + K ak x k
n
n=
k
∑
i= 1
ai
1 k
∑ ai xi
n i= 1
20
x
15
10
5
-3
-2
-1
0
1
2
3
y
Abb. 3: Beispiel für einen Medianwert. Der
Medianwert teilt eine Verteilung genau in zwei
Hälften.
Der Zentralwert oder Medianwert stellt ebenfalls einen charakteristischen Lagewert einer
Häufigkeitsverteilung dar. Er wird für bestimmte statistische Verfahren benötigt. Er teilt die
Häufigkeitsverteilung flächengleich auf, so dass sich links und rechts vom Zentralwert genau
gleich viele Ereignisse befinden. Der häufigste Wert oder Modalwert stellt, wie sein Name schon
sagt, den Wert mit der größten Häufigkeit dar. Er ist also der Gipfel ("Peak") in einer
Häufigkeitsverteilung.
15
VERSUCH 1: STATISTIK UND DATENVERARBEITUNG
600
Mittelwert
Median
Modalwert
Häufigkeit / Klasse
500
400
300
200
100
0
0.00
0.25
0.50
0.75
1.00
1.25
1.50
1.75
2.00
Klassenmitten
Abb. 4: Beispiel für eine nicht symmetrische
Verteilung. Beachte die Lage von Mittelwert,
Median und Modalwert.
In einer Normalverteilung (Gaußverteilung, Abb. 5) sind infolge der Symmetrie der Verteilung
arithmetischer Mittelwert, Medianwert und Modalwert identisch.
STATISTISCHE VERTEILUNGEN
G AUSSVERTEILUNG, P OISSONVERTEILUNG
1.0
0.8
y
0.6
0.4
0.2
0.0
-6σ
-5σ
-4σ
-3σ
-2σ
-1σ
µ
1σ
2σ
3σ
4σ
5σ
6σ
x
Abb. 5: Normalverteilung (vergl. Abb. 1) mit
Angabe des Mittelwertes µ=0 und der
Standardabweichung σ
Als Beispiele für theoretische, stetige Häufigkeitsverteilungen sollen die Normalverteilung
(Gaußsche Glockenkurve) und die Poissonverteilung als Beispiel für eine schiefe Verteilung
besprochen werden. Viele Messwerte aus Experimenten sind nach diesen beiden theoretischen
Mustern verteilt. Die Normalverteilung (Abb. 5) wurde von Gauß im Zusammenhang mit der
Theorie der Messfehler eingeführt. Aus verschiedenen Gründen ist sie die wichtigste stetige
Verteilung:
1. Viele Zufallsvariablen, die bei Experimenten und Beobachtungen auftreten, sind
normalverteilt.
16
PHYSIKALISCH-TECHNISCHE METHODEN IN DER BIOLOGIE
2. Andere Zufallsvariablen sind annähernd normalverteilt. In vielen Fällen führt dann die
Annahme einer Normalverteilung zu sinnvollen und praktisch brauchbaren Ergebnissen.
3. Gewisse, nicht normalverteilte Variablen lassen sich auf einfache Weise so transformieren,
dass die sich daraus ergebende Variable normalverteilt ist.
Die Funktionsgleichung der Gaußverteilung lautet:
f ( x) =
1  x− µ 

σ 
− 
1
e 2
2π σ
2
µ = Mittelwert σ = Standardabweichung
Die Standardabweichungen σ sind definitionsgemäß die Wendepunkte der Glockenkurve,
projiziert auf die x-Achse (Abb. 5). Im Bereich zwischen ±σ liegen 68% aller beobachteten Werte.
Im Bereich±2σ liegen 95,5% und im Bereich ±3σ
so gut wie alle Werte, nämlich 99,7%.
Die Standardabweichung σ ist ein Maß für die Streuung der Werte um den Mittelwert µ Je größer
die Standardabweichung, desto weiter streuen also die Werte um den Mittelwert (Abb. 5). Die
Summenhäufigkeitsfunktion oder Verteilungsfunktion (Integral der Glockenkurve) ergibt eine
Sigmoide (Abb. 2).
100
σ =1
σ =2
σ =3
80
f(x)
60
40
20
0
-6
-4
-2
0
2
4
6
x
Abb. 6: Normalverteilungen mit
Mittelwert
und
verschieden
Standardabweichungen.
gleichem
großen
Ein Beispiel für eine schiefe diskrete Verteilung ist die Poissonverteilung (Abb. 7) mit der
Funktionsgleichung:
f ( x) =
µ x −µ
e
x!
Für Mittelwerte nahe Null kann sich die Poissonverteilung einer abnehmenden
Exponentialfunktion nähern, für größere Mittelwerte kann sie in eine Normalverteilung
übergehen (Abb. 7).
17
VERSUCH 1: STATISTIK UND DATENVERARBEITUNG
0.40
0.35
µ =1
µ =5
µ = 10
0.30
y
0.25
0.20
0.15
0.10
0.05
0.00
0
5
10
15
20
x
Abb. 7: Poissonverteilungen mit unterschiedlich
großen Mittelwerten. Für µ= 1: Annäherung an
eine Exponentialverteilung; für µ = 10:
Annäherung an Normalverteilung
SCHLIESSENDE STATISTIK – STATISTISCHE TESTS
Neben der bloßen Beschreibung unserer Daten liefern statistische Verfahren auch Methoden,
welche uns erlauben, vernünftige Entscheidungen im Falle von Ungewissheit zu treffen, und
Maßzahlen zu erhalten, die für Schlussfolgerungen, Prognosen und Entscheidungen verwendet
werden können. Solche Verfahren nennt man statistische Tests.
Statistische Tests überprüfen bestimmte (vorgegebene) Annahmen über die Verteilung einer
Grundgesamtheit anhand von Daten aus einer oder mehreren Stichproben. Bei
wissenschaftlichen Untersuchungen muss man meist Vergleiche anstellen. Man möchte z.B.
wissen, ob sich zwei Stichproben (Mittelwerte und Standardabweichungen) tatsächlich, d.h.
signifikant, oder nur rein zufällig unterscheiden (Abb. 8). Das prinzipielle Vorgehen bei diesen
Tests ist dabei stets ähnlich:
18
•
Zunächst wird aufgrund z.B. einer Theorie eine Annahme über die Verteilung bzw.
Verteilungen der beteiligten Grundgesamtheiten formuliert (z.B. die Verteilungen
besitzen gleichen Mittelwert). Diese Annahme nennt man Nullhypothese. Zu einer
Nullhypothese darf es nur genau eine weitere Möglichkeit geben, die Alternativhypothese
dass die Nullhypothese nicht zutrifft. Hierbei gilt zu beachten, dass es nicht für jede
beliebige Nullhypothese auch entsprechende Testverfahren gibt. Man sollte sich daher
bereits im Vorfeld überlegen, was man realistisch testen kann!!!
•
Danach erhebt man mit Hilfe von Zufallstafeln, Zufallsgeneratoren o.Ä. einen Satz
randomisierter Stichproben aus den zu untersuchenden Grundgesamtheiten (z.B. unseren
Bohnensäckchen). Umfang und Art dieser Stichproben richten sich nach der Fragestellung
bzw. dem vorgesehenen Test. Bei Messungen gilt jede Einzelmessung als ein Wert und
entsprechende Messserien (z.B. 5× 1 mL mit einer bestimmten Pipette abmessen)als
Stichprobe.
•
Das statistische Testverfahren liefert nun aus den erhobenen Stichproben Maßzahlen für
die Wahrscheinlichkeit des Zutreffens der Nullhypothese.
PHYSIKALISCH-TECHNISCHE METHODEN IN DER BIOLOGIE
•
Je nach Wertigkeit des Problems wird eine statistische Signifikanzschwelle festgelegt.
Diese ergibt sich aus der Wahrscheinlichkeit an, dass die Nullhypothese abgelehnt wird
obwohl sie zutrifft. Üblich sind Irrtumswahrscheinlichkeiten von 5% (meist mit signifikant
bezeichnet) und 1% (meist mit hoch signifikant bezeichnet).
•
Liegen die ermittelten Maßzahlen über der Schwelle, so wird die Nullhypothese
angenommen, liegen sie darunter wird sie verworfen und die Alternativhypothese wird
angenommen. Man sollte aber beachten, dass eine Ablehnung der Nullhypothese noch
keinen schlüssigen Beweis für die Alternativhypothese erbringt. Statistische Tests lassen
sich in ihrer Logik nicht umkehren! Mit Statistik lassen sich also keine Beweise führen, nur
Hypothesen bekräftigen.
Es sei hier auch noch einmal ausdrücklich darauf hingewiesen dass die Signifikanzschwellen
mathematisch völlig willkürlich sind und eher eine gesellschaftlichen Konsens über ein Restrisiko
darstellen. Je nach Problemstellungen können auch Irrtumswahrscheinlichkeiten von 10-6 noch
inakzeptabel hoch sein (z.B. bei Medikamenten oder im Hochsicherheitsbereich von
Kernreaktoren).
120
Häufigkeit / Klasse
100
80
60
40
20
0
-5.0
-2.5
0.0
2.5
5.0
7.5
10.0
Klassenmitten x
Abb. 8: Normalverteilungen mit unterschiedlich
großen
Mittelwerten
(zwei
verschiedene
Stichproben)
und
gleich
großen
Standardabweichungen.
Man kann statistische Tests grob in verteilungsabhängige und verteilungsunabhängige Tests
einteilen. Bei verteilungsabhängigen Tests muss die Art der Verteilung (z.B. Normalverteilung)
bekannt sein oder sie wird vorausgesetzt. Als Beispiel soll wieder das Gewicht der Bohnen
dienen. Zwei Stichproben derselben Bohnensorte werden sich nur rein zufällig, d.h. nicht
signifikant voneinander unterscheiden, während sich zwei unterschiedliche Bohnensorten
tatsächlich, d.h. signifikant unterscheiden könnten. Um das zu prüfen, muss eine Bewertung für
die Differenz zweier arithmetischer Mittelwerte ( ∆ x = x1 − x 2 ) aus zwei Stichproben über
dasselbe
Merkmal
Standardabweichung
gefunden
sd
werden.
Dabei
wird
auch
für
diese
Differenz
eine
gebildet, die sich aus den beiden Standardabweichungen der beiden
Mittelwerte berechnen lässt:
19
VERSUCH 1: STATISTIK UND DATENVERARBEITUNG
sd2 = sx21 + sx22
Die Genauigkeit, die man für die Unterscheidung zweier Stichproben vorgibt, wird durch
Vielfache der Standardabweichung angegeben. Als Konvention wird üblicherweise folgende
Klassifizierung anerkannt:
DER T-TEST
∆ x ≥ 2, 576 × sd
•
:Abweichung ist wahrscheinlich signifikant
(Vertrauensintervall für s > 99%)
•
1, 96 × sd ≤ ∆ x < 2, 576 × sd
•
∆ x < 1, 96 × sd
: keine sichere Aussage möglich
: Abweichung ist wahrscheinlich zufällig
(Vertrauensintervall für s < 95%)
NACH
STUDENT
Der sogenannte t-Test nach Student beruht auf der t-Verteilung, die von W.S. Gosset unter dem
Pseudonym Student veröffentlicht wurde. Mit dem t-Test wird geprüft, ob die Mittelwerte
und
x2
s1
mit ihren Standardabweichungen
s2
und
x1
zweier normalverteilter Stichproben
(Voraussetzung beim t-Test) gleich oder verschieden sind (Abb. 8).
t=
x1 − x 2
sd
Das Ergebnis dieses Tests ist eine Fehlerwahrscheinlichkeit α in %, die angibt, ob der
Unterschied der beiden Stichproben signifikant ist. Oft ist es nicht möglich, in beiden Messreihen
den gleichen Probenumfang herzustellen, dann liegt also n1 ≠ n2 vor. Bei kleineren Messreihen
(unter 50 Varianten) oder bei Unterschieden zwischen n1 und n2 von mehr als 5 - 10 % muss dies
berücksichtigt werden. Man verwendet dann die Berechnungsformel:
t=
n1n2 ( n1 + n2 − 2 )
n1 + n2
x1 − x 2
( n1 − 1) s12 + ( n2 − 1) s22
Auch hier sind die wichtigsten Zahlenwerte schon aus den Berechnungen der Mittelwerte und
Standardabweichungen der einzelnen Proben bekannt.
Die weitere Auswertung erfolgt mit einer t-Tafel (siehe Tabellenwerke der Statistik) oder mit
einem t-Wert-Diagramm, in dem die t-Werte, die α-Werte und die Anzahl der Freiheitsgrade
tabellarisch oder graphisch dargestellt sind. Mit dem berechneten Wert für t und der Anzahl der
Freiheitsgrade (m = n1+n2-2) kann man die Fehlerwahrscheinlichkeit ablesen. Zur Beurteilung
des Versuchsergebnisses gilt:
20
•
α< 0,01: Es besteht ein signifikanter Unterschied zwischen den Proben
•
α < 0,05: Mit großer Wahrscheinlichkeit besteht ein Unterschied
•
α > 0,05: Ein Unterschied ist nicht anzunehmen
PHYSIKALISCH-TECHNISCHE METHODEN IN DER BIOLOGIE
•
PAARE
α > 0,5 : Sehr wahrscheinlich besteht kein Unterschied
VON
MESSUNGEN, REGRESSION, KORRELATION
Bisher sind Zufallsexperimente behandelt worden, in denen nur eine einzelne Variable x vorkam.
Bei Problemen mit zwei Variablen (x, y) prüft man meist, ob eine Beziehung zwischen den
Variablen besteht und welcher Gesetzmäßigkeit sie folgt. So kann man beispielsweise nach der
Abhängigkeit zwischen Durchmesser x und Gewicht y bei Bohnen fragen. In der Analysis heißt y
dann eine Funktion von x. In der Statistik spricht man stattdessen von der Regression y bezüglich
x. Diese nichts sagende Beziehung (Regress = Rückschritt) hat sich leider allgemein eingebürgert
und erhalten besser ist der Ausdruck Ausgleichsrechnung oder Kurvenanpassung. Interessiert
man sich nur für die Beziehung zwischen x und y, ohne nach der Abhängigkeit zu fragen, so
spricht man von der Korrelation zwischen x und y.
REGRESSIONSGERADE, PRINZIP
DER KLEINSTEN
QUADRATE
Liegt eine Stichprobe von Beobachtungen (x1,y1), (x2,y2), ... (xn, yn) aus einer zweidimensionalen
Grundgesamtheit vor, so trägt man sie am besten in ein kartesisches Koordinatensystem ein ().
Man erhält dann entweder eine Punktwolke oder einen mehr oder weniger guten
Zusammenhang der Punkte, die vielleicht schon optisch eine Gerade ergeben könnten. Man
könnte dann subjektiv eine Ausgleichsgerade oder Regressionsgerade durch die Punkte zeichnen
und zu einem beliebigen x-Wert den zugehörigen y-Wert ablesen (Abb. 9).
40
Daten
Regressionsgerade
35
30
y
25
20
15
10
5
0
0
2
4
6
8
10
x
Abb. 9: Regressionsgerade
liegende Punkte.
durch
verstreut
Liegen die Punkte jedoch nicht mehr so ideal, so werden verschiedene Personen im Allgemeinen
verschiedener Meinung darüber sein, wie die Ausgleichsgerade zu legen ist. Um subjektive
Einflüsse auszuschalten, muss wieder eine objektive Methode herangezogen werden. Eine solche
ist das Gaußsche Prinzip der kleinsten Quadrate (least squares). Es besagt bezüglich der
Regressionsgerade (lineare Regression) folgendes:
•
Die Gerade y = a x + b ist so zu legen, dass die Summe der Quadrate aller Abstände der
Punkte von der Geraden möglichst klein (Minimum) wird (Abb. 9).
•
Unter dem Abstand eines Punktes von einer Geraden versteht man üblicherweise die
Länge des Lotes von dem Punkt auf die Gerade, also den senkrechten Abstand. Man
21
VERSUCH 1: STATISTIK UND DATENVERARBEITUNG
benutzt aber aus rechentechnischen und theoretischen Gründen den Abstand parallel zur
y-Richtung. Beide sind trigonometrisch einfach ineinander umrechenbar.
•
Die Summe der Abstände wird minimal,
Regressionsgeraden wie folgt berechnet:
wenn
man
die
Steigung
a
der
 n

 ∑ xi − yi  − nx y

a =  i= 1 n

2
2
 ∑ xi  − nx
 i= 1 
•
Der Achsenabschnitt b der Regressionsgeraden berechnet sich mit dieser Steigung a:
b = y − ax
Man kann sich die Suche nach dem Minimum mit einem Modell aus der Mechanik anschaulich
erklären (siehe Modell Regressionsgerade). Die Regressionsgerade stellt einen Stab dar, auf den
von den einzelnen Punkten aus Kräfte, vermittelt durch Gummiringe (bzw. Federn), einwirken.
Die Gummiringe müssen dabei parallel zur y-Richtung gehängt werden. Der Stab bewegt sich
automatisch in eine Lage, in der das Gesamtdrehmoment auf ihn gleich Null ist, d.h. der Stab
kommt zur Ruhe. Diese Lage entspricht genau dem gesuchten Minimum für die Summe der
Abstände und somit der theoretisch berechneten Regressionsgeraden. Als Maß dafür, wie gut die
einzelnen Punkte eine Gerade ergeben, wie gut sie also korrelieren, dient der
Korrelationskoeffizient r. Er berechnet sich nach:
2
 n

 ∑ ( xi − x ) ( y i − y ) 

r = n i = 1
n
2
2
∑ ( xi − x ) ∑ ( yi − y )
i= 1
i= 1
Der Wert für r bewegt sich zwischen -1 und +1.
•
r = -1 : Regressionsgerade mit negativer Steigung und beste Korrelation der Messwerte.
•
r = 0 : Die Messwerte zeigen überhaupt keine Korrelation.
•
r = +1 : Regressionsgerade mit positiver Steigung und beste Korrelation der Messwerte.
Viele Taschenrechner besitzen auch eine direkte Möglichkeit zur statistischen Berechnung von
Regressionsgeraden. Sie geben als Ergebnis die Steigung a, den Achsenabschnitt b und den
Korrelationskoeffizienten r aus.
Der Vollständigkeit halber soll noch erwähnt werden, dass es auch nichtlineare Regressionen für
beliebige Funktionsgleichungen nach unterschiedlichen Verfahren gibt. Da sie rechnerisch
aufwendig sind, werden sie meist mit Computerprogrammen (Statistiksoftware) realisiert.
Außerdem gibt es noch die Möglichkeit, verschiedene Funktionen in Geraden zu transformieren
und dann eine lineare Regression durchzuführen. Hierbei muss man jedoch beachten, dass die
Abstände von den Punkten zur Kurve entsprechend mittransformiert werden. Man spricht bei
22
PHYSIKALISCH-TECHNISCHE METHODEN IN DER BIOLOGIE
dieser Art der Regression auch von Anpassung, Ausgleichsrechnung oder Kurvenfitting (kurz
Fitting). Alle Begriffe bringen zum Ausdruck, dass theoretische Kurven an vorhandene
Messwerte angepasst werden sollen.
EXPERIMENTELLER TEIL
DATENVERARBEITUNG
UND
MODELLIERUNG
MIT
MICROSOFT EXCEL™
Der Versuchsteil „EXCEL“ zielt darauf ab, Ihnen den Einstieg in die Behandlung von Messwerten
mit Hilfe einfacher Datenerfassungsprogramme zu erleichtern. Mit der Tabellenkalkulation
„EXCEL“ können auf einfache Weise Messreihen textlich und graphisch dargestellt werden. Hier
seien nur aufgeführt: Datenreihen, Tabellen, einfache Graphen, Säulendiagramme, Histogramme
und Boxplots. Als alternative Programme bieten sich wissenschaftliche Graphik- und StatistikPakete an, z.B. ORIGIN, SIGMAPLOT, SPSS und STATISTICA.
DER
ERSTE
KONTAKT
MIT EINEM
„SPREADSHEET“
Üben Sie unter Anleitung ihres Praktikumsassistenten folgende Operationen:
•
Erstellen eines Arbeitsblattes.
•
Füllen einzelner Spalten mit Daten.
•
Markieren und Verschieben einzelner Spalten.
•
Copy und Paste (Kopieren – Einfügen).
•
Löschen von einzelnen Daten.
EINFACHE FORMELN
•
Entwickeln Sie ein Arbeitsblatt, in dem in einer von Ihnen frei gewählten Spalte eine
monoton zunehmende Zahlenreihe von 1 bis 1000 erstellt werden kann. (z.B. mit den
Schrittweiten 1 und 5: 0,1,2,3,4… 1000 bzw. 0, 5, 10, 15, 20, 25 … 1000).
•
Addieren Sie alle Zahlen der Zahlenreihe 1, 2, 3, 4, … 1000. Vergleichen Sie Ihr Ergebnis
mit der Gauß’schen Formel:
 n+ 1
i = n

 2 
i= 1
n
∑
•
Generieren Sie die Reihe 2n von 1 bis 100. Sortieren Sie die Spalte in absteigender
Reihenfolge.
•
Generieren Sie eine zufällige Zahlenreihe.
RELATIVE
UND ABSOLUTE
BEZÜGE
RELATIVE BEZÜGE
Werden Formeln kopiert, passt EXCEL Zelladressen, die sich in den zu kopierenden Zellen
befinden, im Zielbereich automatisch an ihre neue Position an. Adressen bzw. Bezüge die beim
kopieren automatisch angepasst werden, heißen daher „relative“ Bezüge. Die Adressen der
23
VERSUCH 1: STATISTIK UND DATENVERARBEITUNG
Formel sind abhängig von der Position der Formelzelle! (Relative Bezüge werden meist bei
einfachen und übersichtlichen Rechnungen verwendet. Beim „Kopieren“ und „Einfügen“ werden
die Adressen automatisch verwaltet.
ABSOLUTE BEZÜGE
Absolute Bezüge bleiben mit den ursprünglichen Koordinaten erhalten. Sie enthalten vor der
Spalten- bzw. Zeilenbezeichnung ein Dollarzeichen $. Absolute Bezüge werden häufig bei der
Verwendung von Formeln verwendet.
Zellbezug in der
Ursprungsformel
A1
$A$1
A$1
$A1
●
Bezugart
Zellbezug in der kopierten
Formel
Relativer Zellbezug: Beide Teile der B2
Adresse werden kopiert und angepasst.
Absolute Spalten und Zeilen-Adressen: $A$1
Beim Kopieren wird nichts verändert.
Absolute Zeilenadresse: Beim Kopieren B$1
wird
nur
der
Spaltenbuchstabe
angepasst.
Absolute Spaltenadresse: Beim Kopieren $A2
wird nur die Zeilennummer angepasst.
Füllen Sie die Felder B5 und F5 mit zwei beliebigen Zahlen. Berechnen Sie B5-F5 und
$B$5-$F$5. Kopieren Sie die einzelnen Funktionen in neue Felder.
SIMULATION
DER
RATENGLEICHUNG
MIT EINER
TABELLENKALKULATION
Selbst bei einfachen Ratengleichungen (z.B. Zustand A geht in einer bestimmten Zeit über in
Zustand B und zerfällt weiter in Zustand C) treten Differenzialgleichungssysteme auf, die sich oft
nur mit ausgefeilten mathematischen Fähigkeiten analytisch lösen lassen. Mit EXCEL ist es
möglich, die Gleichungen auf anschauliche und einfache Weise numerisch zu lösen und
graphisch darzustellen.
In unserem Praktikum sollen Sie die einfache Ratengleichung A → B (z.B. Radioaktiver Zerfall,
oder exponentielles Wachstum einer Bakterienkultur) numerisch lösen und graphisch
visualisieren.
ETWAS MATHEMATIK
Für die numerische Lösung von Differentialgleichungen muss man die Gleichungen so
umwandeln oder vereinfachen, dass sich das Problem mit einem digitalen Rechner berechnen
lässt.
Die Ratengleichung für den Übergang
A  λ→ B
lautet
24
PHYSIKALISCH-TECHNISCHE METHODEN IN DER BIOLOGIE
dA ( t )
= − λ A( t)
dt
Diese Gleichung können Sie mathematisch lösen, für eine rechnerische Lösung mit dem
Computer eignet sie sich aber noch nicht, da der Rechner keine Möglichkeit besitzt die
infinitesimal kleinen Differentiale darzustellen. Stattdessen verwenden wir eine Näherungslösung
indem wir die Gleichung umschreiben und die Differentiale in Differenzen umwandeln
∆ A ( t)
= − λ A( t)
∆t
c
∆ A ( t) = − λ ∆ t A ( t)
Tabellenkalkulationen eignen sich besonders für sog. rekursive Berechnungen bei denen ein Wert
sich jeweils aus dem vorhergehenden ergibt d.h.
A ( t + ∆ t) = f ( A ( t) )
Für unseren Fall ergibt sich
A ( t + ∆ t) = A ( t) + ∆ A ( t)
= A ( t) − λ ∆ t A ( t)
= A ( t) ( 1 − λ ∆ t)
FORMULIERUNG
•
IN
EXCEL
Festlegen des Zeitintervalls ∆t, der Geschwindigkeitskonstante λ und der Anfangsmenge
A(0): z.B. ∆t = 5, λ = 0.035 und A(0) = 100.
•
Generieren einer Zeitreihe mit der festgelegten Schrittweite. z.B. 20 Schritte
•
Iterative Berechnung von A(t).
•
Graphische Darstellung Ihres Ergebnisses mit linearer und logarithmischer Skalierung.
•
Ändern der Zeitkonstanten.
•
Erneute iterative Berechnung von A(t)
•
Graphische Darstellung Ihres Ergebnisses mit linearer und logarithmischer Skalierung.
•
Vergleichen Sie Ihr Ergebnis mit der analytischen Lösung der Differenzialgleichung:
A ( t ) = A0 e− λ t
Warum haben wir den Ansatz für unsere rechnerische Lösung als Näherung bezeichnet?
AUSWAHL
STATISTISCHER
Funktion
ANZAHL()
FUNKTIONEN:
Argumente
Zellbezüge/ Werte
Beschreibung
Anzahl der Zahlen in der Argumentenliste bzw.
den Bereichen
25
VERSUCH 1: STATISTIK UND DATENVERARBEITUNG
ANZAHL2()
Zellbezüge/ Werte
MAX()
MEDIAN()
MIN()
MITTELWERT()
STABW()
Zellbezüge/ Werte
Zellbezüge/ Werte
Zellbezüge/ Werte
Zellbezüge/ Werte
Zellbezüge/ Werte
STABWN()
Zellbezüge/ Werte
STFEHLERXY()
Zellbezüge/ Werte
AUSWAHL
MATHEMATISCHER
FUNKTIONEN
Funktion
ABS()
Argumente
Zahl
EXP()
FAKULTÄT()
KÜRZEN()
LN()
LOG()
Zahl
Zahl
Zahl
Zahl
Zahl; Basis
LOG10()
Zahl
PI()
keine
PRODUKT()
Zellbereich/ Werte
REST()
Zahl; Divisor
RUNDEN()
Zahl; Stellenanzahl
SUMME()
Zahlen/ Zellbereich
WURZEL()
positive Zahl
ZUFALLSZAHL()
keine
ZUFALLSZAHL()* keine
100
KÜRZEN(ZUFAL keine
LSZAHL()*100)
26
Anzahl
der
gefüllten
Zellen
in
der
Argumentenliste bzw. den Bereichen
Größter Zahlenwert der Liste bzw. der Bereiche
Median der angegebenen Zahlen/Bereiche
Kleinster Wert des Zahlenbereichs
Durchschnittswert der Zahlen bzw. der Bereiche
Berechnet die Standardabweichung ausgehend
von einer Stichprobe
Berechnet die Standardabweichung ausgehend
von der Grundgesamtheit
Standardfehler bei der linearen Regression
Beschreibung
Absolutwert der Zahl (ohne Vorzeichen)
Expotentialfunktion: e hoch Zahl
Fakultät der Zahl
Schneidet die Nachkommastellen ab
Natürlicher Logarithmus zur Basis e
Logarithmus der Zahl zur angegebenen Basis,
ohne Angabe der Basis wird 10 als Basiswert
genommen
Natürlicher Logarithmus zur Basis 10
Die Kreiskonstante Pi mit einer Genauigkeit von
15 Stellen
Produkt der Zahlen in der Liste oder dem
Bereich
Ermittelt den Divisionsrest
Die Zahl wird kaufmännisch gerundet. Falls die
Stellenanzahl
negativ
ist,
wird
dem
entsprechend vor dem Komma gerundet
Summe der Zahlenliste bzw. der Zahlen im
Bereich
Quadratwurzel der Zahl
Liefert nach jeder Neuberechnung
Zufallszahl >=0 und <1
Zufallszahl zwischen 0 und 100
Ganzzahlige Zufallszahl zwischen 0 und 100
eine
PHYSIKALISCH-TECHNISCHE METHODEN IN DER BIOLOGIE
GRAPHISCHE DATENVERARBEITUNG
MIT
MICROCAL ORIGIN™ 5.0
Origin ist ein graphisch orientiertes Analysesystem für Messdaten. Mit diesem Programm soll
beispielhaft der Umgang mit naturwissenschaftlicher Software in Verbindung mit den aus
Experimenten gewonnenen Daten gezeigt werden.
Solch eine Software erleichtert die Arbeit erheblich, da sie Daten schnell statistisch verarbeiten
und auch sofort veröffentlichungsreif ausdrucken kann. Man kann die Daten schnell
transformieren, korrelieren oder einer entsprechenden Regression unterziehen. Die Gefahr dabei
ist, dass man sich oft nicht darüber im Klaren ist, was dabei genau passiert. Aus dem “Fitten” der
Kurve kann dann sehr schnell ein “passend machen” der Kurve werden.
Nachfolgend sind einige Möglichkeiten aufgeführt, die mit dieser Software bearbeitet werden
können. Sämtliche Möglichkeiten können über ein “Menue” vom Benutzer aufgerufen werden.
Die Eingabe der Daten kann über die Tastatur oder aus einer Vielzahl von Dateiformaten
erfolgen. Die Daten können vielfältig transformiert werden:
•
Änderung von Größe und Skalierung der Darstellung
•
Lineare, halblogarithmische oder doppelt logarithmische Darstellung
•
Punktdarstellung, Linienzüge oder Balkendiagramme
•
Darstellung mit Kartesischen oder Polarkoordinaten
•
Fast Fourier Transformation
Weiterhin sind statistische Analysen und Kurvenanpassungen mit Angaben der Fehlergrenzen an
die Daten möglich. Der Benutzer hat die Möglichkeit aus zahlreichen internen Funktionen
auszuwählen oder selbst Funktionen zu definieren. Außerdem ist das Integrieren und
Differenzieren von Kurven möglich. In jedem Bearbeitungsstadium können die Daten graphisch
ausgegeben werden.
GRÖSSENVERTEILUNG
VON
ZELLKULTUREN
Zwei verschiedene Zellkulturen sollen bezüglich ihrer Größe (Durchmesser, evtl. auch Volumen)
statistisch analysiert und verglichen werden. Dazu wurden von jeder Zellkultur mit einer
Mikroskopkamera Bilder erstellt (siehe auch 5), die Sie nun ausmessen werden. Die Zellkulturen
wurden vor der Bildaufnahme mit Trypsin behandelt wodurch sie sich von ihrem
Wachstumssubstrat abgelöst haben und nun nahezu ideal rund wurden.
•
Machen Sie Ausdrucke von den Bildern und bestimmen Sie jeweils den größten und
kleinsten Durchmesser der Zellen mit einem Lineal. Alternativ können Sie diese Messung
auch in einem Bildverarbeitungsprogram wie ImageJ vornehmen. Tragen Sie die beiden
Größen in eine Urliste z.B. in einer Excel-Tabelle oder in Microcal Origin ein.
•
Wenn Sie hinreichend viele (wie viele sind das?) Zellen vermessen haben berechnen Sie
den mittleren Durchmesser und das mittlere Zellvolumen als das Volumen eines
Rotationselypsoids um die Achse des längsten Durchmessers.
27
VERSUCH 1: STATISTIK UND DATENVERARBEITUNG
•
Bestimmen Sie mit den Statistikfunktionen Mittelwert, Varianz, Standardabweichungen
und Standardfehler für beide Größen. Vergleichen Sie die beiden Zellkulturen
•
Bestimmen Sie die Verteilung des mittleren Durchmessers und des Zellvolumens anhand
eines Histogramms. “Fitten” Sie dieses Histogramm mit einer Gaussverteilung. Damit
kann die Normalverteilung der Werte überprüft werden. Das ist für den t-Test wichtig, da
er als verteilungsabhängiger Test eine Normalverteilung voraussetzt.
•
Vergleichen Sie die beiden Zellkulturen mittels des t-Tests. Sind beide wirklich gleich
groß. Was passiert, wenn Sie ihren Stichprobenumfang vergrößern?
LITERATUR
1. Bosch, K.: Elementare Einführung in die Wahrscheinlichkeitsrechnung, Vieweg
Studium Basiswissen, Braunschweig, 1986
2. Bosch, K.: Elementare Einführung in die angewandte Statistik, Vieweg Studium
Basiswissen, Braunschweig, 1987
3. Hopp, V., Berninger, G.: Mathematische Funktionen zur Beschreibung von Vorgängen in
Natur und Technik, GIT Fachz. Lab. 8, 682-691, 1987
4. Kreyszig E.: Statistische Methoden und ihre Anwendungen, Vandenhoeck u. Ruprecht,
Göttingen, 1975
5. Müller, G.W., Kick, T.: Basic-Programme für die angewandte Statistik,
R.Oldenburg Verlag, München, 1985
6. Sachs, L.: Angewandte Statistik, 9. Auflage. Springer Verlag, Heidelberg, 1999
7. Vogel, A.: Funktionstafeln und statistische Tabellen, Verlag Konrad Wittwer, Stuttgart,
1979
8. Wallis W.A., Roberts H.V.: Methoden der Statistik, rororo, 1969
28