Vorschau - Netzwerk Lernen

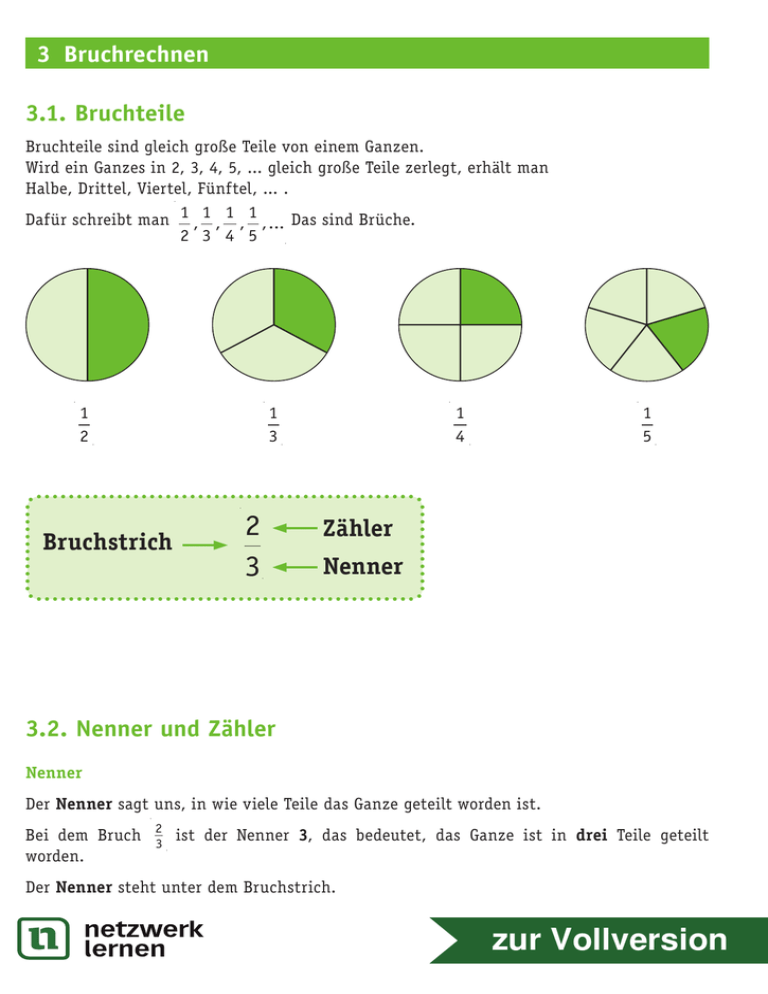
3 Bruchrechnen
3.1. Bruchteile
Bruchteile sind gleich große Teile von einem Ganzen.
Wird ein Ganzes in 2, 3, 4, 5, ... gleich große Teile zerlegt, erhält man
Halbe, Drittel, Viertel, Fünftel, ... .
Dafür schreibt man 1 , 1 , 1 , 1 ,... Das sind Brüche.
2 3 4 5
฀
1
2
฀
Bruchstrich
2
3
O
V
฀
1
4
S
R
฀
U
A
H
C
1
3
฀
1
5
฀
Zähler
Nenner
3.2. Nenner und Zähler
Nenner
Der Nenner sagt uns, in wie viele Teile das Ganze geteilt worden ist.
Bei dem Bruch
worden.
2
3
ist der Nenner 3, das bedeutet, das Ganze ist in drei Teile geteilt
Der Nenner steht unter dem Bruchstrich.
฀
zur Vollversion
3 Bruchrechnen
3 Bruchrechnen
Wenn man einen Bruch am Zahlenstrahl darstellen will, teilt man die Strecke zwischen zwei
natürlichen Zahlen in so viele Teile, wie im Nenner stehen.
)4
2
3
Erweitern mit 4
2
3
2 4
3 4
8
12
1
10
฀
฀
0฀
฀
฀
2
10
H
C
฀
)3
3
4
Erweitern mit 3
3
4
฀
2
3
฀
฀
3
4
8
12
9
12
9
12
<
O
V
Brüche können auch durch Kürzen gleichnamig gemacht werden.
฀
฀
฀
฀
3.6. Darstellung von Brüchen am Zahlenstrahl
2
3
฀
<
3
4
0
18
<1
unechte Brüche
1
10
12
5
฀
5
10
11
2
฀
1
2
; 2
10 10
1
;
5
1
10
1
5
1
2
3
1 10
1 52 1 21
฀
฀
฀ Subtraktion von Brüchen
3.7.
Addition
und
Addition von gleichnamigen Brüchen
฀
+
4
8
+
=
1
8
=
5
8
+
>1
฀
1
Mathe – clever gelernt!
10
฀
1
1
2
13
Je weiter rechts am Zahlenstrahl ein Bruch angeordnet ist, desto größer ist er.
Auf einem Zahlenstrahl kann man jede natürliche Zahl und jeden Bruch einem Punkt
zuordnen.
echte Brüche
1
฀
0
S
R
฀
8
12
฀0
9
12
)3
9
12
3 3
4 3
5
10
)4
8
12
1
5
฀
U
A
2
10
4
8
฀
1
8
5
8
Mathe – clever gelernt!
฀
฀
Gleichnamige
Brüche werden
addiert, indem man die Zähler
addiert und den Nenner beibehält.
19
zur Vollversion
3 Bruchrechnen
3 Bruchrechnen
Multiplikation von Brüchen mit ganzen Zahlen
•
Waldemar macht von Montag bis Freitag täglich eine
3
4
Zähler mal Zähler
Nenner mal Nenner
Wie viele Stunden sind das in einer Woche?
3
4
5
3
4
3
4
3
4
5
3 5
4
3
4
15
4
3
4
3
4
15
4
33
4
oder
U
A
Stunde Hausaufgaben.
฀
฀
4
Waldemar macht in den 5 Tagen 3 3 Stunden Hausaufgaben.
4
฀
Der Nenner wird beibehalten.
Multiplikation von Brüchen miteinander
S
R
2
3
4 von 5
4
5
O
V
15
15
Das ganze Rechteck besteht aus
฀ 15 Teilen, also 1 =
.
Die grüne Teilfläche des Rechtecks ist wieder ein Rechteck, dessen eine Seite
andere 4 Einheiten lang ist. Es besteht aus 8 Teilen, also 8 .
5
15
฀
2
3
Werden mehrere Brüche miteinander multipliziert, schreibt man sie auf einen langen Bruchstrich. Bevor man dann multipliziert, sollte man kürzen.
H
C
Ein Bruch wird mit einer ganzen Zahl multipliziert, indem man den Zähler mit der
ganzen Zahl multipliziert.
฀
฀
8
15
•
33
฀
2 von 3
4 2
5 3
2 · 8 · 15 = 2 · 1 · 15 = 2 · 1 · 3 = 2 · 1 · 1 = 2
9
5 · 9 · 24
1·9·1
1·9·3
5·9·3
Wichtig: Man kann immer nur eine Zahl aus dem Zähler mit einer Zahl aus dem
Nenner gleichzeitig kürzen. Anschließend kann man weiter kürzen – auch mit schon
gekürzten Zahlen. Die Zahlen, die man kürzt, streicht man durch.
und dessen
Dieses Ergebnis muss auch bei der Berechnung der Fläche herauskommen.
Für das grüne Rechteck gilt also
฀
4 2
5 3
4 2
5 3
8
15
฀
฀
Ein Bruch wird mit einem Bruch multipliziert, indem man die
฀
Zähler miteinander und die Nenner miteinander multipliziert.
22
Mathe – clever gelernt!
Mathe – clever gelernt!
23
zur Vollversion