Übungen zu Kathetensatz, Höhensatz und Satz des Pythagoras

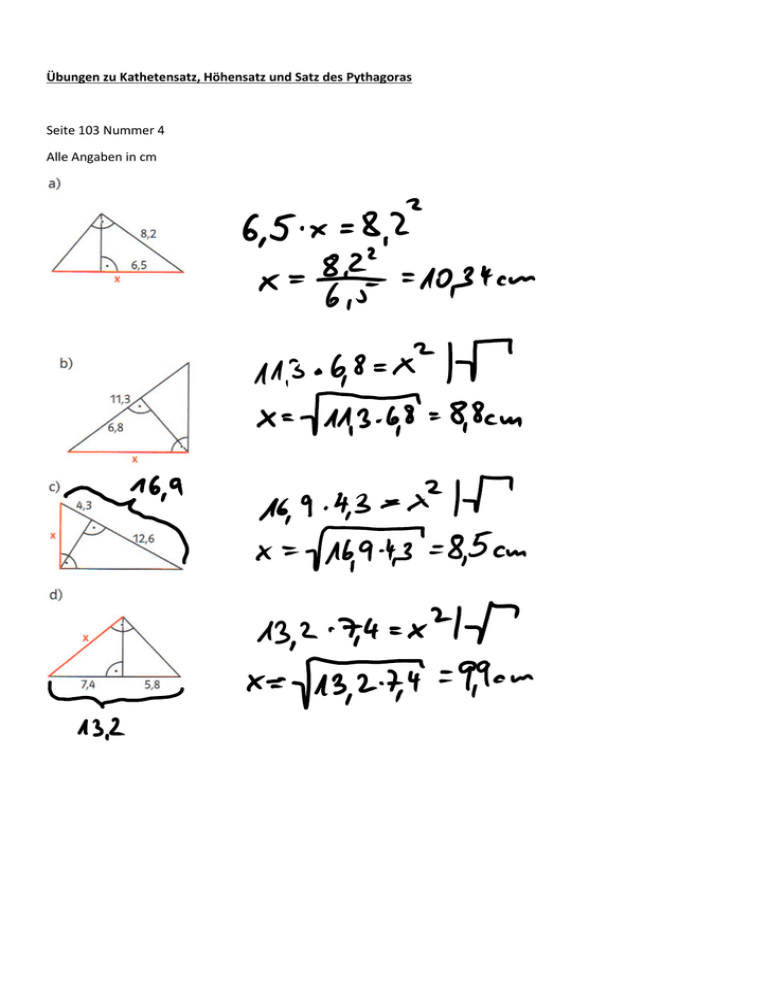
Übungen zu Kathetensatz, Höhensatz und Satz des Pythagoras
Seite 103 Nummer 4
Alle Angaben in cm
Seite 105 Nr.1
Formuliere den Höhensatz
Tipp: Das Quadrat der Höhe auf der Hypotenuse ist gleich dem Produkt der beiden Hypotenusenabschnitte.
x²=m∙n
r²=a∙b
̅̅̅̅ ∙ 𝐴𝐷
̅̅̅̅
̅̅̅̅ 2 = 𝐶𝐷
𝐵𝐷
̅̅̅̅̅
𝑇𝑊 2 = ̅̅̅̅̅
𝑅𝑊 ∙ ̅̅̅̅̅
𝑊𝑆
Nummer 6
Berechne die Länge der Strecke x. (Alle Maße in cm)
x² = 7,9 ∙ 3,6
𝑥 = √7,9 ∙ 3,6 = 5,33 𝑐𝑚
x² = 15,3 ∙ 8,4
𝑥 = √15,3 ∙ 8,4 = 11,34 𝑐𝑚
9,5² = 6,2 ∙ (x-6,2) |:6,2
𝑥 − 6,2 =
𝑥=
9,5²
+
6,2
9,5²
6,2
| +6,2
6,2 = 20,76 𝑐𝑚
x² = 14,7 ∙ (20,9 – 14,7)
x² = 14,7 ∙ 6,2
𝑥 = √14,7 ∙ 6,2 = 9,55 𝑐𝑚
Satz des Pythagoras
Seite 107 Nummer 5
Denkweise: Die Summe der Quadrate über den Katheten ist gleich dem Quadrat über der Hypotenuse.
 (4cm)²+20cm² = x²
16cm²+20cm² = x²
36cm² = x² |√
6cm = x
(12cm)² + x² = 169cm²
144cm² + x² = 169cm² | -144cm²
x² = 25cm² |√
x = 5cm
x² + x² = 50cm²
2x² = 50cm² | :2
x² = 25cm² |√
x = 5cm
x² + 49cm² = (25cm)²
x² + 49cm² = 625cm² |-49cm²
x² = 576cm² |√
x = 24cm
Seite 108 Nummer 10
81+144 = 225
225 = 225 √
(5; 12; 13)  5²+12²=13²
25+144=169
169=169 √
(24; 7; 25)  24²+7²=25²
576+49=625
625=625√
(17; 15; 8)  15²+8² = 17²
225+64=289
289=289 √
(9; 40; 41)  9²+40²=41²
81+1600=1681
1681=1681 √
(10; 24; 26)  10²+24²=26²
100+576=676
676=676 √
a) (9; 12; 15)  9²+12²=15²
(3*3)²+(3*4)²=(3*5)²
Für alle Zahlen lässt sich das so nicht überprüfen.
(n*3)²+(n*4)²=(n*5)²
Da man für n jede Zahl einsetzen kann, könnte man so die Aussage für alle Vielfache überprüfen.
9n²+16n²=25n²
25n² = 25n²
√
Da das Ergebnis eine wahre Aussage ist, gilt die Aussage, dass alle Vielfache von (3; 4; 5) ein pythagoräisches Tripel
darstellen.
13
24
60
24
123
√522 − 482 =20
√1222 − 222 = 120
√1132 − 1122 = 15