V - FH Dortmund
Werbung

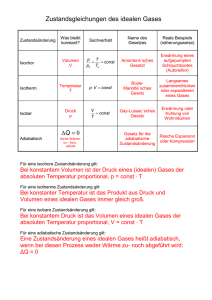
Physik III im Studiengang Elektrotechnik - 1. Hauptsatz der Thermodynamik - Prof. Dr. Ulrich Hahn WS 2008/09 Energieerhaltung Erweiterung des Energieerhaltungssatzes der Mechanik berführbar Erfahrung: verschiedene Energieformen sind ineinander überfü der Energieträ Energieträger kann wechseln mechanische Arbeit Wärme R. Mayer (1842) mechanisches Wä Wärmeä rmeäquivalent J. Joule (1850) Wärme mechanische Arbeit Dampfmaschine aber: 2. Hauptsatz es gibt keine reibungsfreie Bewegung esgibt gibtkein keinPerpetuum PerpetuumMobile Mobile(1. (1.Art)! Art)! es 1. Hauptsatz 2 Formulierungen des 1. Hauptsatzes H. v. Helmholtz (1847): in einem abgeschlossenen System bleibt die Gesamtenergie konstant Gesamtenergie innere Energie Nicht zur inneren Energie gehören: ⇒ U = const. ; ∆U = 0 Epot des Systems Ekin des Systems nicht geschlossene Systeme: H. v. Helmholtz: 1. Hauptsatz es gibt keine Maschine, die stä ständig Arbeit abgibt ohne Energie aufzunehmen 3 Änderung der inneren Energie geschlossene Systeme: System U Energie makroskopisch geordnete Bewegung: mechanische Arbeit W reversibel Kolbenbewegung irreversibel Rührer mikroskopisch ungeordnete Bewegung Wärme Q irreversibel Heizung Wärmeleitung Konvektion Strahlung offene Systeme: System U 1. Hauptsatz Materie Energie makroskopisch geordnete Bewegung Ekin des Massenstroms mikroskopisch ungeordnete Bewegung T des Massenstroms 4 U : Zustandsgröße? Kreisprozess (geschlossenes System): Folge v. Zustandsänderungen mit ZE = ZA U1´= U3 + E13 P1, V1, T1 U1 E21 = W21 + Q21 System: P, V, T P2, V2, T2 U2 W Q U2 = U1 + E21 E32 = W32 + Q32 E13 = W13 + Q13 P3, V3, T3 U3 U3 = U2 + E32 Umlauf: System ist wieder im Zustand 1: System: Perpetuum Mobile U1´ < U1: System gibt Energie ab U1´ > U1: Umgebung gibt Energie ab Umgebung: Perpetuum Mobile 1. Hauptsatz U1´ = U1 ; ∆U = 0 5 Zustandsgröße U Kreisprozeß: ∆U = 0 ⇒ U ist Zustandsgröß Zustandsgröße öße beliebige Zustandsänderung: ∆U = U 2 − U1 unabhängig von der Art der Zustandsänderung 1. Hauptsatz fü für geschlossene Systeme: ∆U = Qzu + Wzu − Qab − Wab Prozessgrößen ößen Wärme, mechanische Arbeit: Prozessgröß abhängig von der Art der Zustandsänderung Konvention: dem System zugeführte Energien: > 0 vom System abgegebene Energien: < 0 1. Hauptsatz 6 Kreisprozesse I ∆U = 0 = Qzu − Qab + Wzu − Wab Wärmekraftmaschine Kühlschrank, Wärmepumpe ≠0 >0 ≠0 < 0 Wärme mech. Arbeit <0 > 0 mech. Arbeit Wärme Prozess oder Zustandsänderung: zeitliche Folge von Ereignissen Kausalitä Kausalität: vorausgehende Ereignisse nachfolgende Ereignisse System wechselwirkt mit der Umgebung irreversibel Ausgleichsprozess reversibel Umkehrung ohne Änderung der Umgebung immer im Gleichgewicht quasistatisch 1. Hauptsatz 7 Wärmekapazität Änderung von U: System: P, V, TA Q System: P, V, TE Änderung der Temperatur des Systems Ausnahmen: Änderung des Aggregatzustandes isotherme Zustandsänderung Welche Temperaturänderung bewirkt Q? dQ = C ⋅ dT C: Wä Wärmekapazitä rmekapazität des Systems Q: Prozessgröße ⇒ C: Prozessgröße J [C ] = K C spezifische W. definieren: cs := C = C(m) oder C(ν) m C abhängig vom Material C molare W. cm := C = C(T) ν 1. Hauptsatz 8 Wärmekapazität idealer Gase isochore Zustandsänderung: Q dQ V =const = CV ⋅ dT CV : isochore Wärmekapazitä rmekapazität Qicr = TE ∫C V TA 1. Hauptsatz ⋅ dT = ∆U gilt fü für beliebige Prozesse TA TE 9 Wärmekapazität idealer Gase isobare Zustandsänderung: dQ P =const = C P ⋅ dT CP : isobare Wärmekapazitä rmekapazität zusätzlich: Gasvolumen ändert sich Temperaturänderung, mechanische Arbeit dQibr = dU + P(V ) ⋅ dV C P = CV + ν ⋅ R Häufig verwendet: Enthalpie P = const W VE, TE VAP,TA P Q cPm = cVm + R cPs = cVs + Rs Qibr = ∆U + P ⋅ ∆V = ∆(U + P ⋅V ) = C P ∆T = ∆H H := U + P ⋅ V 1. Hauptsatz 10 Innere Energie ungeordnete Bewegung Molekularbewegung im idealen Gas: Moleküle: Massenpunkte Wechselwirkung: Kollisionen untereinander, mit Gefäßwand große Molekülzahl: statistische Betrachtung 1 Molekül (eindimensional): Impulsübertrag auf die Gefäßwand: Strom von Molekülen (eindimensional): ∆p = 2 ⋅ mM ⋅ v⊥ Kraft auf die Gefäß Gefäßwand äßwand Druck im Gefäß Gefäß Schwerpunkt des Gases ruht: F N ⋅ mM 2 1 v⊥ N (v x ) = N ⇒ P = = A V 2 1. Hauptsatz 11 thermische Energie P= Bewegung der Moleküle kinetische Energie N ⋅ 2 ⋅ Ekin, x V Geschwindigkeiten der Moleküle mittlere kinetische Energie ⇒ P ⋅ V = N ⋅ 2 ⋅ Ekin, x = N ⋅ k ⋅ T eindimensionale Bewegung: 1 Freiheitsgrad d. Molekü Moleküls Ekin, x ungeordnete Bewegung Temperatur 1 = ⋅ k ⋅T 2 thermische Energie Freiheitsgrad 3-dim. Gefäße: Druck Kräfte in x, y, z - Richtung Bewegung in x, y, z - Richtung gleich wahrscheinlich N/3 in x-, N/3 in y-, N/3 in z - Richtung 1. Hauptsatz Ekin, x 1 = ⋅ Ekin 3 Ekin 3 = ⋅ k ⋅T 2 12 Freiheitsgrade Translation: 3 Freiheitsgrade Gleichverteilungssatz: Gasgemische: ImMittel Mittelweisen weisenalle alleFreiheitsgrade Freiheitsgrade Im diegleiche gleichethermische thermischeEnergie Energieauf auf die schwere Moleküle fliegen langsamer! Moleküle: ausgedehnte Objekte Rotation um Schwerpunkt (elastische) Deformation Rotation: 3 Hauptträgheitsachsen 3 Freiheitsgrade 2 Freiheitsgrade lineare Moleküle: Jz << Jx, Jy Schwingung: 1. Hauptsatz E pot = Ekin 2 Freiheitsgrade/Feder 1 EM = ( fT + f R + f S ) ⋅ k ⋅ T 2 13 Wärmekapazität – innere Energie f f ideales Gas: U = N k ⋅ T = ν ⋅ R ⋅ T 2 2 dU = CV ⇒ dT cVm = f R 2 isochoreWärmekapazität Wärmekapazität Freiheitsgrade Freiheitsgrade Molek Molekülstruktur isochore ülstruktur leicht meßbar: Adiabatenexponent Clement-Desormes Rüchardt Flammersfeld Gas f +2 CP = κ := f CV cVm cPm κ }f=3 }f = 5 } f=7 1. Hauptsatz f=6 f>7 f=6 14 Ausfrieren von Freiheitsgraden Temperaturabhängigkeit von CV: + Schwingung + Rotation Translation kleine Temperaturen: Rotation und Schwingung fallen aus kT < Emin r h Rotation: | L | = l ⋅ , l ∈ ℵ Emin Quantenphysik 1. Hauptsatz 2 1 Schwingung: E = h ⋅ ω ⋅ (n + ); n ∈ ℵ 2 15 Wärmekapazität von Kristallen thermische Ausdehnung nicht behindern thermische Ausdehnung klein: kinetische Theorie: ⇒ c = 3⋅ R m V Krä Kräfte C P ≈ CV Atome schwingen in 3 Dimensionen f = 6 J = 24 ,93 mol ⋅ K unabhä unabhängig vom Material Dulong – Petit - Regel gültig für: hohe Temperaturen schwere Elemente Ausfrieren d. Freiheitsgrade: kollektive Schwingungen (Wellen, Phononen) 1. Hauptsatz 16 Wärmekapazität von Flüssigkeiten „lockere“ Bindung der Moleküle unterschiedliche Bewegungsmöglichkeiten Zahl der Freiheitsgrade unbestimmt CP, CV nur experimentell bestimmbar 1. Hauptsatz Wasser: guter Wärmespeicher 17 Kalorimetrie Messung der Wärmekapazität von Festkörpern oder Flüssigkeiten abgeschlossenes System (Thermosgefäß) Flüssigkeit, c1 bekannt 2 Subsysteme Meßobjekt, c2 unbekannt TE Anfangszustand: Temperaturunterschied Endzustand: thermisches Gleichgewicht T2 System 1: T1 T1 Q1 Q2 Q1 = C1 ⋅ (TE − T1 ) = − Q2 System 2: T2 = − C2 ⋅ (TE − T2 ) n n Subsysteme im abgeschlossenen System: c2s = 1. Hauptsatz m1 ⋅ c ⋅ (TE − T1 ) m1 ⋅ (T2 − TE ) s 1 ∑Q i =1 i =0 Richmannsche Mischungsregel 18 spezielle Zustandsänderungen idealer Gase reversible Prozesse geschlossene Systeme Energietransfer Wärme Volumenänderungsarbeit VE r r r r = − P ⋅ dV WV = ∫ F • ds = ∫ P ⋅ da • ds ∫ VA Betrachtung im Arbeitsdiagramm P P(V ) WV VA 1. Hauptsatz VE V 19 isotherme Zustandsänderung T=const T=const Zustandsänderung bei T = const unabhängige Zustandsgröße: V P, V T=const BoyleBoyle-Mariotte: Mariotte: P ⋅V = const T=const 1 P(V ) = ν ⋅ R ⋅ T ⋅ V VE WV = − ∫ P(V ) ⋅ dV VA V = −ν ⋅ R ⋅ T ⋅ ln( E ) VA T = const ⇒ ∆U = 0 = WV + Q VE Q = −WV = ν ⋅ R ⋅ T ⋅ ln( ) VA was an Wärme aufgenommen wird, wird an mechanischer Arbeit abgegeben 1. Hauptsatz 20 isochore Zustandsänderung P, T, V = const Zustandsänderung bei V = const unabhängige Zustandsgröße: T Q GayGay-Lussac: Lussac: P = const. T VE WV = − ∫ P(V ) ⋅ dV = 0 VA TE Q = ∫ CV ⋅ dT = ν ⋅ c ⋅ (TE − TA ) m V TA 1. Hauptsatz f = ν ⋅ R ⋅ ⋅ (TE − TA ) = ∆U 2 21 isobare Zustandsänderung Zustandsänderung bei P = const unabhängige Zustandsgröße: T V, T P=const GayGay-Lussac: Lussac: V = const. T Q VE WV = − ∫ P(V ) ⋅ dV = − P ⋅ (VE − VA ) VA TE Q = ∫ C P ⋅ dT TA 1. Hauptsatz f +2 ⋅ (TE − TA ) = ν ⋅ c ⋅ (TE − TA ) = ν ⋅ R ⋅ 2 m P 22 adiabatische Zustandsänderung Zustandsänderung ohne Wärmeaustausch unabhängige Zustandsgröße: V P(V), T(V) @ Q = 0 1. Hauptsatz: dU = CV ⋅ dT= − P (V , T ) ⋅ dV ( +dQ ) ν ⋅ R ⋅ T (V ) ⇒ CV ⋅ dT = − ⋅ dV V TE ⋅VEκ−1 = TA ⋅ VAκ−1 1. Hauptsatz DGL, gesuchte Funktion: T(V) T ⋅ V κ−1 = const. P ⋅ V κ = const.' T κ ⋅ P1−κ = const.' ' Poissonsche Gleichungen W = ν ⋅ cVm ⋅ (TE − TA ) = PE ⋅VE − PA ⋅VA κ −1 23 polytrope Zustandsänderung isotherme, -chore, -bare, adiabatische Zustandsänderung: Idealisierung realer Zustandsänderungen isotherm: perfekter Wärmekontakt mit der Umgebung adiabatisch: kein Wärmekontakt mit der Umgebung realer Prozeß Prozeß: isobar: isochor: 1. Hauptsatz P ⋅V n = const. P ⋅ V 1 = const. P ⋅V κ = const . 1 ≤ n ≤ κ n : Polytropenexponent perfekter Druckausgleich mit der Umgebung P ⋅ V 0 = const . kein Druckausgleich mit der Umgebung P 0 ⋅V = const . PA ⋅ VA VE 1−n W= ⋅ (( ) − 1) n − 1 VA n=0 n∞ 1 1 Q = ν ⋅ R ⋅ (TE −TA ) ⋅ ( − ) κ −1 n −1 24