Mathematik – Neue Wege Lineare Algebra – Analytische Geometrie
Werbung

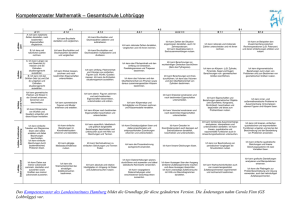
Mathematik – Neue Wege Lineare Algebra – Analytische Geometrie (85584) Einordnung von NEUEN WEGEN in den Rahmenplan Mathematik für das Gymnasium und die Stadtteilschule in Hamburg Die folgende Übersicht zeigt, wie MATHEMATIK - NEUE WEGE zur Umsetzung des Rahmenplans beitragen kann und Grundlage für einen schuleigenen Arbeitsplan sein kann. Modul 3 – Matrizen und Vektoren als Datenspeicher Lösen linearer Gleichungssysteme, Modellieren einfacher Verflechtungen und diskreter Wachstumsprozesse Inhalt Rahmenplan Hamburg Umgang mit den üblichen Verknüpfungen zwischen Vektoren und Matrizen: Vektoraddition, Multiplikation mit Skalar, Skalarprodukt als Rechenoperation mit n-Tupeln Umgang mit den üblichen Verknüpfungen zwischen Vektoren und Matrizen: Addition und Multiplikation von Matrizen, Multiplikation einer Matrix mit einem Skalar, Multiplikation von Matrix und Vektor Modellieren einfacher diskreter Wachstumsprozesse mit Populationsmodellen; Erklären derer Besonderheiten (Einteilung der Population in Altersgruppen, Rekursivität), auch im Hinblick auf andere Wachstumsmodelle; Berechnen von Aussagen zum Wachstum über eine und zwei Zeitperioden und Aussagen zum Langzeitverhalten, z.B. Aussterben, Stabilisierung, unbegrenztes Wachstum (z.B. durch Vorgabe von Potenzen der Populationsmatrix), periodisches Verhalten der Population Modellierung einfacher Verflechtungen (betriebswirtschaftliche Modelle) Erstellen und lösen linearer Gleichungssysteme mit dem Gauß’schen Eliminationsverfahren innerhalb verschiedener Sachkontexte und die Lösungen sachgerecht deuten Untersuchung des Langzeitverhaltens Inhalt Neue Wege Lineare Algebra – Analytische Geometrie 1.2 Bewegen im Raum – Vektoren 3.1 Skalarprodukt und Winkel Anmerkungen Leitidee Algorithmus 4.1 Von Tabellen zu Matrizen – Matrizen in Anwendungen Leitidee Algorithmus 4.2 Übergangsprozesse Leitidee Modellieren Leitidee Algorithmus 4.1 Von Tabellen zu Matrizen – Matrizen in Anwendungen 4.2 Übergangsprozesse 2.1 Geraden in der Ebene und im Raum 4.2 Übergangsprozesse Leitidee Modellieren Leitidee Algorithmus 4.2 Übergangsprozesse Nur Kurse auf erhöhtem Niveau Mathematik – Neue Wege Lineare Algebra / Analytische Geometrie (Bestell-Nr. 85584) Leitidee Modellieren Leitidee Algorithmus 1 Modul 6 – Analytische Geometrie Umgang mit Vektoren und damit gebildeten Objekten im Anschauungsraum Inhalt Rahmenplan HH Geometrische Objekte in einem Schrägbild darstellen Geraden und Ebenen (letztere in Parameter- und Koordinatenform) im Raum beschreiben. Untersuchen von einfachen Lagebeziehungen der genannten geometrischen Objekte Messen der Länge eines Vektors sowie Abstand und Winkel zwischen geometrischen Objekten (außer bei windschiefen Geraden) mithilfe des Skalarproduktes; In geeigneten Fällen Bestimmung mit elementargeometrischen Methoden Erweiterung der geometrischen Deutung der Lösungsmenge lineare Gleichungssysteme Arbeiten mit Kugeln im Anschauungsraum Inhalt Neue Wege Lineare Algebra – Analytische Geometrie 1.1 Orientieren im Raum – Koordinaten 1.2 Bewegen im Raum – Vektoren 2.1 Geraden in der Ebene und im Raum 2.2 Ebenen im Raum 2.1 Geraden in der Ebene und im Raum 2.2 Ebenen im Raum 3.1 Skalarprodukt und Winkel 3.2 Winkel zwischen Geraden und Ebenen 3.3 Abstandsprobleme 2.2 Ebenen im Raum 3.2 Winkel zwischen Geraden und Ebenen 5.1 Kreise und Kugeln 5.2 Kegelschnitte Mathematik – Neue Wege Lineare Algebra / Analytische Geometrie (Bestell-Nr. 85584) Anmerkungen Leitidee Raum und Form Vektoren algebraisch und geometrisch Koordinatendarstellung Rechnen mit Vektoren Lineare Abhängigkeit/Unabhängigkeit Leitidee Raum und Form Gerade/Ebene in Punkt-RichtungsForm und Koordinatenform Leitidee Raum und Form Gauß-Algorithmus Leitidee Algorithmus Leitidee Messen Leitidee Raum und Form Skalarprodukt Normalenvektor Strategien zur Abstandsbestimmung Leitidee Algorithmus Leitidee Messen Leitidee Raum und Form Nur Kurse mit erhöhtem Niveau 2