Vorlesung 6

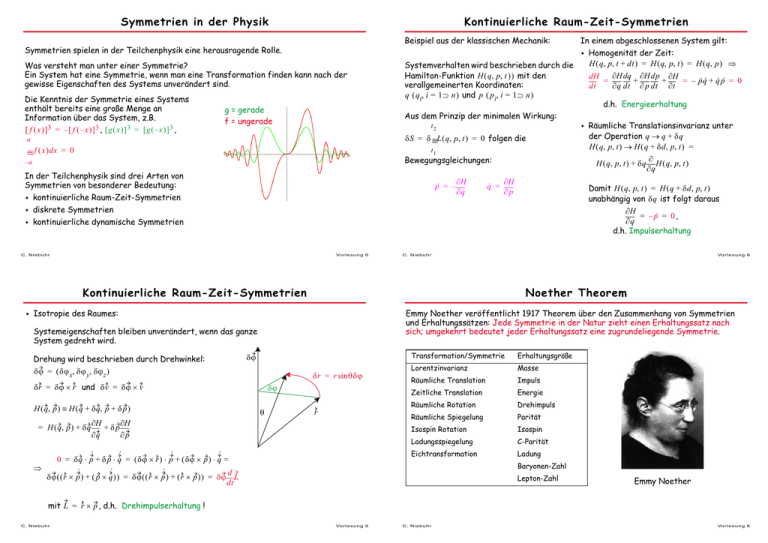
Symmetrien in der Physik
Kontinuierliche Raum-Zeit-Symmetrien
Beispiel aus der klassischen Mechanik:
Symmetrien spielen in der Teilchenphysik eine herausragende Rolle.
• Homogenität der Zeit:
Was versteht man unter einer Symmetrie?
Ein System hat eine Symmetrie, wenn man eine Transformation finden kann nach der
gewisse Eigenschaften des Systems unverändert sind.
Die Kenntnis der Symmetrie eines Systems
enthält bereits eine große Menge an
Information über das System, z.B.
[ f ( x ) ] 3 = –[ f ( – x ) ] 3 , [ g ( x ) ] 3 = [ g ( – x ) ] 3 ,
g = gerade
f = ungerade
Systemverhalten wird beschrieben durch die
Hamilton-Funktion H ( q, p, t ) ) mit den
verallgemeinerten Koordinaten:
q ( q i, i = 1…n ) und p ( p i, i = 1…n )
Aus dem Prinzip der minimalen Wirkung:
t2
δS = δ ∫ L ( q, p, t ) = 0 folgen die
a
∫
f ( x ) dx = 0
t1
Bewegungsgleichungen:
–a
In der Teilchenphysik sind drei Arten von
Symmetrien von besonderer Bedeutung:
ṗ = –
• kontinuierliche Raum-Zeit-Symmetrien
∂H
∂q
q̇ =
∂H
∂p
• diskrete Symmetrien
Vo r l e s u n g 6
der Operation q → q + δq
H ( q, p, t ) → H ( q + δd, p, t ) =
∂
H ( q, p, t ) + δq H ( q, p, t )
∂q
Vo r l e s u n g 6
Noether Theorem
• Isotropie des Raumes:
Emmy Noether veröffentlicht 1917 Theorem über den Zusammenhang von Symmetrien
und Erhaltungssätzen: Jede Symmetrie in der Natur zieht einen Erhaltungssatz nach
sich; umgekehrt bedeutet jeder Erhaltungssatz eine zugrundeliegende Symmetrie.
Systemeigenschaften bleiben unverändert, wenn das ganze
System gedreht wird.
δϕ
δϕ = ( δϕ x, δϕ y, δϕ z )
δr = r sin θδϕ
δr = δϕ × r und δv = δϕ × v
∂H
∂H
+ δp
∂q
∂p
• Räumliche Translationsinvarianz unter
C. N i e bu h r
Kontinuierliche Raum-Zeit-Symmetrien
= H ( q, p ) + δq
d.h. Energieerhaltung
∂H
= – ṗ = 0 ,
∂q
d.h. Impulserhaltung
C. N i e bu h r
H ( q, p ) ≡ H ( q + δq, p + δ p )
H ( q, p, t + dt ) = H ( q, p, t ) = H ( q, p ) ⇒
∂H dq ∂H dp ∂H
dH
=
+
+
= – ṗq̇ + q̇ ṗ = 0
∂q dt ∂ p dt ∂t
dt
Damit H ( q, p, t ) = H ( q + δd, p, t )
unabhängig von δq ist folgt daraus
• kontinuierliche dynamische Symmetrien
Drehung wird beschrieben durch Drehwinkel:
In einem abgeschlossenen System gilt:
δϕ
θ
r
˙
˙
˙
˙
0 = δq ⋅ p + δ p ⋅ q = ( δϕ × r ) ⋅ p + ( δϕ × p ) ⋅ q =
⇒
˙
˙
˙
d
δϕ ( ( r × p ) + ( p × q ) ) = δϕ ( ( r × p ) + ( r × p ) ) = δϕ L
dt
Transformation/Symmetrie
Erhaltungsgröße
Lorentzinvarianz
Masse
Räumliche Translation
Impuls
Zeitliche Translation
Energie
Räumliche Rotation
Drehimpuls
Räumliche Spiegelung
Parität
Isospin Rotation
Isospin
Ladungsspiegelung
C-Parität
Eichtransformation
Ladung
Baryonen-Zahl
Lepton-Zahl
Emmy Noether
mit L = r × p , d.h. Drehimpulserhaltung !
C. N i e bu h r
Vo r l e s u n g 6
C. N i e bu h r
Vo r l e s u n g 6
Eigenschaften von Symmetrieoperationen
Drehimpuls in der Quantenmechanik
Beispiel gleichseitiges Dreieck: Rotationen um ±120° sowie Spiegelungen an den Achsen
führen das Dreieck in sich selber über. Allgemein bildet die Menge der Symmetrieoperationen eine mathematische Gruppe mit den folgenden Eigenschaften:
1. Abgeschlossenheit: Ri, Rj Element ⇒ Rk=RiRj gehört ebenfalls dazu
2. Einselement: IRi=RiI=Rifür alle Ri
3. Inverses: zu jedem Ri gibt es Ri-1, so daß gilt RiRi-1=I
4. Assoziativität: Ri(RjRk)=(RiRj)Rk
x
y
unitär (U†U=1)
SU(n)
nxn
unitär mit Determinante=1
O(n)
nxn
orthogonal
SO(n)
nxn
orthogonal mit Determinante=1
Bosonen (ganzzahliger Spin)
Spin 0
elementar
zusammengesetzt
Vo r l e s u n g 6
Wie addieren sich zwei Drehimpulse J = J 1 + J 2 ?
• Klassisch: Addition der einzelnen Komponenten
’
-3h
’
–
Pseudoskalare
Mesonen
Fermionen (halbzahliger Spin)
Spin 1 (2?)
Spin 1/2
Feldquanten
Quarks, Leptonen
Spin 3/2
Vektormesonen
Baryonenoktett
–
Baryonendekuplett
Vo r l e s u n g 6
Wieder Meson-Beispiel qq - Zustände |1 ⁄ 2 ± 1 ⁄ 2⟩ ⋅ |1 ⁄ 2 ± 1 ⁄ 2⟩
J1
J
können gleichzeitig gemessen werden |J 1 m 1⟩ + |J 2 m 2⟩ = ? |Jm⟩
m = m1 + m2
Der erlaubten Wertebereich ist:
J = J 1 – J 2 , J 1 – J 2 + 1, …, J 1 + J 2 – 1, J 1 + J 2
J2
z.B.
1. Mesonen sind gebundene qq -Zustände. Im Grundzustand ist der Bahndrehimpuls L=0. Beitrag der
Spins zum Gesamtdrehimpuls ?
|1 1⟩ = |1 ⁄ 2 1 ⁄ 2⟩ |1 ⁄ 2 1 ⁄ 2⟩
1
1
Triplett: |1 0⟩ = ------- |1 ⁄ 2 1 ⁄ 2⟩ |1 ⁄ 2 – 1 ⁄ 2⟩ + ------- |1 ⁄ 2 – 1 ⁄ 2⟩ |1 ⁄ 2 1 ⁄ 2⟩
2
2
|1 -1⟩ = |1 ⁄ 2 – 1 ⁄ 2⟩ |1 ⁄ 2 – 1 ⁄ 2⟩
(symmetrisch 1<->2)
1
1
Singlett: |0 0⟩ = ------- |1 ⁄ 2 1 ⁄ 2⟩ |1 ⁄ 2 – 1 ⁄ 2⟩ – ------- |1 ⁄ 2 – 1 ⁄ 2⟩ |1 ⁄ 2 1 ⁄ 2⟩
2
2
(antisymm. 1<->2)
Vgl. tabellierte Werte aus dem PDG Booklet:
- J = 1 ⁄ 2 – 1 ⁄ 2 = 0 d.h. Spin 0: Pseudoskalare Mesonen π, η, K , D
Man kann dies symbolisch
auch schreiben als:
ρ, ω, K* , D*, ...
2. Baryonen sind gebundenen qqq-Zustände. Grundzustand L=0. Spinbeitrag: (qq)q
J = 0+1⁄2 = 1⁄2
2⊗2 = 3⊕1
⇒ mögliche Kombinationen: J = 1 – 1 ⁄ 2 = 1 ⁄ 2 Allgemein: Clebsch-Gordan Koeffizienten
J = 1+1⁄2 = 1⁄2
∑
’
-2h
Beispiel
• Quantenmechanik: nur Betrag und eine Komponente
J 1, J 2
0
-h
C. N i e bu h r
Addition von Drehimpulsen
|Jm⟩ =
h
’
Teilchenklassifizierung nach dem Spin
C. N i e bu h r
JJ J
C mm1 m2 |J 1 m 1⟩ |J 2 m 2⟩ mit
1 2
’
’
Bahndrehimpulse, l , sind ganzzahlig, Spins s können halb- und ganzzahlig sein.
(OTO=1)
- J = 1 ⁄ 2 + 1 ⁄ 2 = 1 d.h. Spin 1 : Vektormesonen
3h
2h
Lˆ2 |lm⟩ = l ( l + 1 ) |lm⟩
Lˆz |lm⟩ = m |lm⟩
m l = – l, – l + 1, …, – 1, 0, +1, …, l – 1, l d.h. ( 2l + 1 ) Möglichkeiten.
Matrizen der Gruppe
nxn
x, y, z
alle drei Komponenten des Drehimpulses gleichzeitig zu messen. Man
kann nur den Betrag L (bzw L 2 ) zusammen mit einer Komponente
(üblicherweise die z-Komponente) messen. Ausserdem sind die
Messwerte quantisiert: so gibt es für L 2 nur die Messwerte:
l ( l + 1 )h 2 mit l = 0, 1, 2, 3, … Für einen bestimmten Wert von l
m l eine ganze Zahl ist im Intervall [ – l, +l ] :
Die meisten der für die Physik interessanten Gruppen sind Matrizengruppen, die
wichtigsten sind:
U(n)
z
z
ergibt eine Messung von L z immer ein Ergebnis der Form m l h 2 wobei
Gruppen sind im allgemeinen nicht kommutativ: RiRk ≠ RkRi
Gruppenname
Für die quantenmechanischen Operatoren des Drehimpulses gilt:
[ L̂ , L̂ ] = ihL̂ und [ Lˆ2, L̂
] = 0 d.h. es ist prinzipiell unmöglich
m 1 + m 2 = m Bedeutung: Wahrscheinlichkeit, dass Jˆ2
zum Quadrat!
Eine 4x4 Matrix ist in einen
3er und einen 1er Block
diagonalisierbar.
den Wert J ( J + 1 ) ergibt für ein System, das aus |J 1 m 1⟩ |J 2 m 2⟩ zusammengesetzt ist.
C. N i e bu h r
Vo r l e s u n g 6
C. N i e bu h r
Vo r l e s u n g 6
Clebsch-Gordan Koeffizienten (PDG)
Symmetrien in der Quantenmechanik
Korrespondenzprinzip in der Quantenmechanik : E → i
∂
∂t
1
p → --- ∇ = ( p̂ x, p̂ y, p̂ z )
i
∂ψ
= Hψ mit Wellenfunktion ψ ( x, t ) .
∂t
Der Erwartungswert eines Operators ist gegeben durch A = ∫ ψ∗ Âψ d 3 x
Schrödingergleichung: i
Beispiel: Der Operator einer räumlichen Translation x → x – δx
∂
D̂ψ ( x, t ) = ψ ( x – δx, t ) = ψ ( x, t ) – δx ψ ( x, t ) = ψ ( x, t ) – iδx ⋅ ( p̂ x ψ ( x, t ) )
∂x
⇒ D̂ = ( 1 – i p̂ x δx ) Frage: vertauschen D̂, H ?
[ D̂, H ]ψ = D̂Hψ – H D̂ψ = H ( x – δx )ψ ( x – δx, t ) – H ( x )ψ ( x – δx, t ) d.h. [ D̂, H ]ψ = 0 wenn
Translationsinvarianz von H gegeben ist: H ( x – δx ) = H ( x ) . Daraus folgt ebenfalls
[ p̂ x, H ( x ) ] = 0 .
Also Translationsinvarianz impliziert Impulserhaltung!
Allgemein gilt: wenn [ Â, H ] = 0 und
d.h. A ist eine Erhaltungsgröße.
C. N i e bu h r
Vo r l e s u n g 6
d
d
∂
 = 0 folgt daraus A = ∫ ψ∗ Âψ d 3 x = 0 ,
dt
dt
∂t
C. N i e bu h r
Vo r l e s u n g 6
Isospin
Erfolge des Isospin-Konzepts
Die Ähnlichkeit von Proton und Neutron veranlasst Heisenberg 1932 zu postulieren, dass
beide nur verschiedene Zustände eines Teilchens, dem Nukleon sind, die sich in der
starken Wechselwirkung identisch verhalten.
mn – m p
939.6 – 938.3
Als Ursache für den geringen Unterschied in der Masse -------------------- = --------------------------------- ≈ 10 – 3
939.6
mn
Erklärung der Multiplettstruktur der Hadronen: Teilchen aus einer horizontalen Reihe
δm ∆
haben alle etwa gleiche Masse (z.B. ---------- ≅ 2 ⋅ 10 – 3 ), sie haben alle den gleichen Isospin I
m∆
und unterscheiden sich nur in I 3 ⇒ es gibt jeweils ( 2I + 1 ) Zustände in einer Reihe.
könnte man die unterschiedliche elektromagnetische Energie vermuten ( m p > m n ??).
1
Heisenberg entwickelt das Konzept des Isospins: das Nukleon hat Isospin I = --- , und die
2
1
1
dritte Komponente I 3 hat die Eigenwerte + --- ("up" für das Proton) und – --- ("down" für das
2
2
Neutron). Mathematisch sind Proton und Neutron Vektoren im Isospinraum: |1 ⁄ 2 1 ⁄ 2⟩ und
|1 ⁄ 2 -1 ⁄ 2⟩ . Die Transformationen bilden die Gruppe SU(2).
Die physikalische Bedeutung besteht im folgenden Postulat:
I3
3 3
|--- – ---⟩
2 2
∆−
S=0
Σ∗0
I, <m>
3 3
|--- ---⟩
2 2
∆++
3 1
|--- ---⟩
2 2
∆+
Σ ∗+
Q=2
Ξ∗−
Ξ∗0
Q=1
3
--2
1230
1
1390
1
--2
1530
0
1670
Ω−
Es handelt sich hier um eine "innere" Symmetrie (Beziehung zwischen Teilchen).
Gemäß dem Noether-Theorem folgt der Erhaltungssatz:
S=–3
Der Isospin ist in der starken Wechselwirkung erhalten
C. N i e bu h r
Σ ∗−
S=–1
S=–2
Die starke Wechselwirkung ist invariant unter Rotationen im Isospinraum.
3 1
|--- – ---⟩
2 2
∆0
Q=0
Einführung der Hyperladung Y :
Y = A+S
mit Baryonenzahl A und
Seltsamkeit S .
Damit ergibt sich folgender
Zusammenhang zwischen
Teilchenladung und der dritten
Komponente des Isospins:
Y
Q = I 3 + --2
die als Gell-Mann Nishijima
Beziehung bezeichnet wird.
Q=–1
Vo r l e s u n g 6
C. N i e bu h r
Vo r l e s u n g 6
Pion-Nukleon-Streuung πN→πN
Es gibt sechs verschiedene elastische
Prozesse
a)
a) π+ + p → π+ + p
c) π- + p → π- + p
e) πo + n → πo + n
b) πo + p → πo + p
d) π+ + n → π+ + n
f) π- + n → π- + n
und vier Prozesse mit Ladungsaustausch:
g) π+ + n → πo + p h) πo + p → π+ + n
i) πo + n → π- + p j) π- + n → πo + n
Da Pion I=1 und Nukleon I=1/2, kann der
Gesamtisospin 3/2 oder 1/2 sein.
Entsprechend gibt es zwei unterschiedliche Amplituden M 3 ⁄ 2 und M 1 ⁄ 2 .
Aus den
ClebschGordanTabellen
ergeben sich
folgende Zerlegungen.
∆-Resonanz in der πN Streuung
a) und f) sind reine I=3/2 Reaktionen : M a = M f = M 3 ⁄ 2 . Die anderen sind Mischungen der
J
m
1
2
2
M j = ------- M 3 ⁄ 2 – ------- M 1 ⁄ 2 . Die Wirkungs3
3
querschnitte stehen im Verhältnis: σ a :σ c :σ j = 9 M 3 ⁄ 2 2 : M 3 ⁄ 2 + 2M 1 ⁄ 2 2 :2 M 3 ⁄ 2 – M 1 ⁄ 2 2
• Wirkungsquerschnitte zeigen bei √s=1230 MeV eine klare Resonanzstruktur: ∆-Resonanz
I=3/2 ⇒ M 3 ⁄ 2 » M 1 ⁄ 2 und
somit σ a :σ c :σ j = 9:1:2
1 1
3 3
a) π+ + p : |1, 1⟩ |---, ---⟩ = |---, ---⟩
2 2
2 2
1 1
23 1
11 1
o
b) π + p : |1, 0⟩ |---, ---⟩ = --- |---, ---⟩ – --- |---, ---⟩
2 2
32 2
32 2
1
1
3
1
1
21 1
c) π- + p : |1, – 1⟩ |---, ---⟩ = --- |---, – ---⟩ – --- |---, – ---⟩
2 2
32 2
32 2
d)
π+ +
1 1
n : |1, 1⟩ |---, – ---⟩ =
2 2
1 1
e) πo + n : |1, 0⟩ |---, – ---⟩ =
2 2
1 1
f) π- + n : |1, – 1⟩ |---, – ---⟩ =
2 2
- für den totalen WQ (c+j)
σ tot ( π + p )
9
------------------------- = ------------ = 3
1+2
σ tot ( π – p )
23 1
11 1
--- |---, – ---⟩ + --- |---, – ---⟩
32 2
32 2
3 3
|---, – ---⟩
2 2
δm/m
SU(2)
sehr gut
2-3%
→
SU(3)
mäßig
+ Charm Quark:
C = +1, Q = 2/3
→
SU(4)
schlecht
+ Bottom Quark:
B = -1,
Q = -1/3
→
SU(5) sehr schlecht
+ Top Quark:
T = +1, Q = 2/3
→
SU(6) ???
Hyperladung:
Y = A + S + C + B + T und Q = I3 + Y/2
N(1520)
⇒ M 1 ⁄ 2 » M 3 ⁄ 2 und es folgt:
pLab (GeV/c)
σ a :σ c :σ j = 0:2:1
√(s) (GeV)
C. N i e bu h r
Vo r l e s u n g 6
SU(4) Multipletts (u,d,s,c)
Symmetrie
+ Strange Quark : S = -1, Q = -1/3
π-pelastic
• Resonanz N(1520) mit I=1/2
Weitere Flavour-Quantenzahlen
n: I3 = -1/2
π-ptotal
π+pelastic
σ ( π + p → ∆ ++ → π + p )
9
-------------------------------------------------------- = --1
σ( π– p → ∆o → π– p )
Vo r l e s u n g 6
Leichte Quarks: Q=I3+A/2 Flavour p: I3 = 1/2
π+ptotal
- für den elastischen WQ
13 1
21 1
--- |---, ---⟩ + --- |---, ---⟩
32 2
32 2
C. N i e bu h r
2
beiden Amplituden, z.B. M c = --- M 3 ⁄ 2 + --- M 1 ⁄ 2
3
3
m1m2
.
Mesonen: qq Zustände
Pseudoskalare
Baryonen: qqq Zustände
40%
SU(3) Untergruppen
(u,d,s)
100%
SU(3) Oktett
u,d,s:
3⊗3 = 8⊕1
• Mesonen (qq) und Baryonen (qqq) lassen sich in Multipletts gruppieren
• beim Isospin war es noch sinnvoll anzunehmen, daß p,n verschiedene Zustände eines
Teilchens (Nukleon) sind
• bereits bei Hinzunahme der Seltsamkeit werden Massensunterschiede in Multipletts
groß: mΞ - mp ≈ 375 MeV. Trotzdem ist das Konzept auch hier wichtig für die
Klassifizierung der Teilchen
C. N i e bu h r
Vo r l e s u n g 6
SU(3) Dekuplett
Vektor Mesonen
C. N i e bu h r
Vo r l e s u n g 6
Quarkmassen
Symmetrie unter Spiegelung
Warum ist Isopsin eine solch gute Symmetrie, der Achtfache Weg (SU(3)) recht
ordentlich und SU(5), SU(6) so schlecht?
Erklärung im Rahmen des Standardmodells: unterschiedliche Quarkmassen
Quarkmassen sind keine direkten Observablen (Confinement). Die relevanten Werte
hängen vom Modell und der jeweiligen experimentellen Situation ab !
z.B. ist die Masse von quasi-freien Quarks in der tiefunelastischen Elektron-ProtonStreuung bei HERA: mu≈md≈einige MeV, dagegen im gebundenen Zustand in Mesonen oder
Baryonen ≈300 MeV (QCD Effekt).
• Bisher gibt es keine befriedigenden
Quarkmassen
Erklärungen für die Massen der Quarks und
Leptonen - sie sind im Standardmodell freie,
mbare
meff/MeV
meff/MeV
Flavour
Baryonen
Mesonen
MeV
willkürliche Parameter
u
4.2
d
7.5
360
310
s
150
c
1100
540
1500
480
b
4200
4700
t
170000
170000
• Die Ursachen für die Massen sind ein
zentrales Thema der theoretischen und
experimentellen Teilchenphysik
• Leptonen: Neutrinooszillationen, Doppelter β-
Zerfall
• Eichbosonen: Suche nach dem Higgsteilchen
am LEP II, LHC, Linear Collider
C. N i e bu h r
Vo r l e s u n g 6
C. N i e bu h r
Vo r l e s u n g 6
Parität - Spiegelsymmetrie
Parität in der Quantenmechanik
Paritätsoperation:
Punktspiegelung = Spiegelung an einer Ebene + Drehung (x,y,z) → (-x,-y,-z)
Paritätsoperator: P̂ψ ( r, t ) = ψ ( – r, t ) und P̂ 2 ψ ( r, t ) = ψ ( r, t )
2
∇
Hamiltonoperator eines freien nichtrelativistischen Teilchens: H = – ------- ⇒ [ H , P̂ ] = 0 , da
2m
Spiegelung
∂
∂
→–
∂x
∂x
Drehung
r → –r
v → –v
grad → – grad
Pseudovektoren (axial):
L→L
(L = r × p)
B→B
(B ∝ j × r)
E → –E
Skalar:
C. N i e bu h r
r⋅r→r⋅r
2
P̂ψ ( r, t ) = P i ψ ( – r, t ) mit P i2 = 1 ⇒ P i = ± 1 intrinsische Parität des Teilchens.
Transformationsverhalten:
Vektoren (polar):
2
∂
∂
→
, d.h. H und P haben simultane Eigenwerte und Eigenfunktionen
∂x
∂x
Für die Kugelfunktionen gilt: Ψ lm ( r ) = R ( r )Y lm ( ϑ, ϕ ) . Die Funktionen Y lm ( ϑ, ϕ ) haben die
Eigenschaft: P̂ ⋅ Y lm ( ϑ, ϕ ) → Y lm ( π – ϑ, π + ϕ ) = ( – 1 ) l Y lm ( ϑ, ϕ ) ⇒ PΨ lm ( r ) = P i ( – 1 ) l Ψ lm ( r )
mit P i = ± 1
• Parität eines Mehrteilchensystems: P̂ ⋅ ψ 1 ⋅ ψ 2 = P 1 ⋅ P 2 ⋅ ( – 1 ) l ⋅ ψ 1 ⋅ ψ 2 , d.h. Parität ist
eine diskrete und multiplikative Quantenzahl.
Pseudoskalar:
• In einer Teilchenreaktion a+b → c+d gilt: P a ⋅ P b ⋅ ( – 1 )
r ⋅ L → –r ⋅ L
Vo r l e s u n g 6
C. N i e bu h r
l ein
= Pc ⋅ Pd ⋅ ( –1 )
l aus
Vo r l e s u n g 6
Parität des Photons
Parität eines Teilchen-Antiteilchen-Systems
Bisher P nur für nicht-relativistische QM diskutiert
- Teilchen und Antiteilchen werden durch verschiedene Wellenfunktionen ( ψ
Klassische Elektrodynamik + Korrespondenzprinzip:
beschrieben, die beide der Schrödingergleichung genügen
1
∇ ⋅ E ( r, t ) = ----- ρ ( r, t )
ε0
Paritätsverhalten:
- kein offensichtlicher Zusammenhang zwischen P
e-
- aus Dirac Gleichung (für Spin 1/2) bzw Klein-Gordon Gleichung (Spin 0) folgt, dass
Paritätserhaltung nur dann gegeben ist wenn:
P f ⋅ P = – 1 für Fermionen
f
P b ⋅ P = +1 für Bosonen
∂
A mit A = Photon in QM
∂t
b
Konsequenz: da Fermionen-Antifermionen nur in Paaren produziert werden, kann mit
paritätserhaltenden Reaktionen nur das Produkt P f ⋅ P bestimmt werden
⇒ A ( r, t ) → P γ A ( r, t ) ⇒ P γ = – 1
f
⇒ willkürliche Wahl: P Quark = – P Antiquark = 1
⇒ im Grundzustand l = 0 :
P(Baryonen)
= (+1)3 = +1
P(Antibaryonen) = (-1)3 = -1
P(Mesonen)
= (-1)(+1) = -1
Vo r l e s u n g 6
Ladungskonjugation: C-Parität
Quantenfeldtheorie: zu jedem Teilchen gibt es ein Anti-Teilchen mit gleichen äußeren
Quantenzahlen ( E, p, r, J , … ) und umgekehrten inneren Quantenzahlen (Ladung, magn.
Moment, L, S, C,...)
Operator:
Ĉ |ψ⟩ ändert innere Quantenzahlen und läßt äußere Quantenzahlen gleich
• meist sind Teilchen keine Eigenzustände von Ĉ , z.B. Ĉ |π +⟩ → π - , aber Ĉ 2 |ψ⟩ = |ψ⟩ ⇒
C2=1
• nur neutrale Bosonen können Eigenzustände von Ĉ sein: z.B. γ,πο,ωο,ϕ nicht Ko, Do
• C-Parität des Photons:
- Ĉ |γ ⟩ = – 1 |γ ⟩ Ĉ dreht Ladungsvorzeichen, also auch A ⇒ -1
• C-Parität des neutralen Pions: πο→γγ
- Ĉ |π o⟩ = Ĉ |γγ ⟩ = +1 |γγ ⟩ ⇒ +1
C. N i e bu h r
e
- dadurch sind e+ und e- miteinander verbunden
Invarianz der Poissongleichung: E ( r, t ) → – E ( – r, t )
C. N i e bu h r
und P
und ψ - )
Relativistische Quantenmechanik: Teilchenerzeugung (vernichtung)
ρ ( r, t ) → ρ ( – r, t )
∇ → –∇
mit E = – ∇φ –
e+
e+
Vo r l e s u n g 6
C. N i e bu h r
Vo r l e s u n g 6