Elastische Verformung, Hooke`sches Gesetz
Werbung

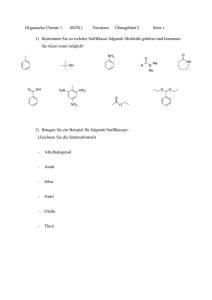
5. Mechanik der deformierbaren Körper (fest, flüssig, gasförmig ) lap5/.../mewae/acsr/Kap5_1/kap5_1_Elast_Deform_s6 20031213 5.0 Allgemein: beobachtete Gesetzmäßigkeiten: zum Großteil aus molekularem Aufbau der Materie abzuleiten. Molekularkräfte: elektrostatischer Natur. Polare Moleküle: el. neutral, aber ± Ladungsschwerpunkte verschieden (z.B. H + OH − quantenmechanisch zu beschreiben! Polare Moleküle können nicht-polare Moleküle vorübergehend polarisieren: ’induzierte Polarisation’ Nicht-polare Moleküle: sind nur im zeitlichen Mittel nicht polar: zeitliche Schwankungen erzeugen Dipol-Moment, die daraus im Mittel resultierenden Kräfte sind ≠ 0. Resultierendes Potential: ”Lennard-Jones-Potential: r Ur = ae − b − cr 6 a b Skizze a...abstoßender Anteil: (Pauli-Prinzip als wesentliche Ursache ): für die meisten physikal. Eigenschaften maßgeblich: ϱ, η, λ, D... b...e..-stat.Anziehung: σ, p 0 .. U ∼ r −6 f = −∇U F ∝ r −7 r max → 10nm Anmerkung zu Dimensionen im atomaren und molekularen Bereich: Skizze Festkörper: geordnete räumliche Struktur (Kristall) ’Fernordnung’: beliebig weit voneinander entfernte Moleküle haben definierten Abstand voneinander, es gibt ’Gitterkonstante’. Moleküle in stabiler Lage in Potentialmulden. Temperatur ≡ Schwingung um die Ruhelage: W kin ≪ −W pot . Festkörper hat definiertes Volumen und definierte Gestalt. Kristall i.a. anisotrop, d.h. physikalische Eigenschaften sind richtungsabhängig. Amorpher Festkörper: keine Kristallstruktur, homogen, isotrop. Amorphe Stoffe: oft besonders hart, zäh, μ, λ.. Flüssigkeiten: höheres W kin der Moleküle, häufiger Platzwechsel ⇒ mittlerer Abstand ≈ r 0 wie beim Festkörper, aber Ort der Moleküle nicht fix: definiertes Volumen, keine def. Gestalt. ’Nahordnung’: Abstand des nächsten Nachbarn ≈ r 0 aber darüber hinaus nicht mehr scharf definiert.Übergang amorpher Festk.-Flüssigkeit ist kontinuierlich, über Zähigkeit und Elastizitätsmodul (beides kommt noch ) definiert. Da temperaturabhängige Größen: fest /flüssig: von Temp. abhängig Teer, Glas, Polymere fließen! Gase: W kin ≪ −W pot : Moleküle verlassen Potentialtopf: füllen jedes Volumen aus: keine definierbare Gestalt, kein definiertes Volumen. 5.1 Elastische Deformation fester Körper: und Hooke’sches Gesetz Deformation: Gestaltsänderung unter Einwirkung einer Kraft. Elast.Deformation: bei Deformation des Körpers werden Gegenkräfte wirksam, die nach Aufhören der äußeren, deformierenden Kraft die Deformationen rückgängig machen. Gesetzmäßigkeit gesucht a aus naivem Modell der Molekülkräfte: Bei Feder: F = −c△x pausibel, wenn Δx hinreichend klein. Dabei war c = cMaterial, Gestalt Jetzt soll Abhängigkeit von Material und Gestalt explizit beschrieben werden. Gesucht also: f(Material)⋅ f(Gestalt) Dehnung: analog zur Feder: F = −c△x ⇒ F ∝ △l aber F = F 1 = F 2 = F 3 ...F i = c△l i = c△n l △l = △l i = n△l i ⇒ wenn n Federn hintereinander angeordnet sind und zum andern um △l ausgedehnt werden, so ist die hierfür erforderliche Kraft F n = 1n F 1 , mit F 1 = c△l ist daei die erfordrliche Kraft, um eine einzelne Feder um △l auszudehnen. F ∝ △nl ∝ △l l da n mit l anwächst. ∑ ′ ′ Bei nebeneinander angeordneten Federn addiert sich die Kraft: F = nF 1 wobei jetzt n ∝ A(Querschnitt) F = const.A △l l F = E ⋅ △l l ⋅ A Hookes’sches Gesetz: F = E △l A l ∗ σ = E⋅ E...Elastitätsmodul F = σ...Zugspannung mN2 ≡ Pascal, Pa A (Feder: A, E, l=const:⇒ F = const.△l (E wäre mit Atomphysik zu berechnen..) E ≡ σ das für Verdoppelung von l △l l = 1, l 2 = l 1 + △l = 2l 1 erforderlich wäre, wenn der Körper sich so weit (und nach dem Hookes’schen Gesetz ) dehnen ließe σ E = △l = σ = P a l Einige Zahlenwerte: (ungefähre Angaben ) Material E Zugfestigkeit ZF σ max △l l max ϱ kPam 3 ϱ kg ZF 1 − 2.10 −3 ∼ 8.10 3 Eisen 100-200 GPa 200 MPa Stahl 100-200 GPa 2 GPa Wolfram 400 Beton 40 50 MPa Nylon 3 300 0.1 1.5 200 140 9.10 −3 0.7 200 Holz II 15 2.10 −2 250 Bemerkenswert Buche ⊥ 1.5 7 Holz ist sehr guter Baustoff: Hohe ZF pro Gewicht! Beispiel: △l l = σ max E z.B. Fe-Draht: A = 1mm 2 : 10 4 Kg 5 N = 10 ≈ G für △l l = 1 für △l l = 10 −3 , für E = 100GPa = 10 mN2 = 10 610N 2 2 mm mm mm 2 2 σ = 100 mmN 2 ≈ 10Kg.g/mm 2 △l l max = 200.10 = 2.10 −3 △l = 2mm für l=1m 100.10 9 (E wird häufig auch in Kp/mm 2 angegeben: praktische Einheit, 1kp=1Kg.g≈10N) Tragkraft dazu: F max = σ max ⋅ A = 2.10 −8 mN2 ⋅ 10 −6 m 2 = 2.10 2 N ≈ 20kg ⋅ g Stahl: F max Stahl ≈ 10 ⋅ F max Fe → △l max Stahl ≈ 10 ⋅ △l max Fe Querkontraktion: Da bei der Dehnung die Dichte des Körpers (und damit sein Volumen) in grober Näherung gleich bleibt, erfährt er zugleich eine Querkontraktion, die der Dehnung proportional ist. △ a = − μ △ l ∗ ∗ a l μ..Poissonkoeffizient Das tatsächlich auftretende △Vist also nicht gleich △l l , sondern wird durch die Querkontraktion verringert, man kann es als fE, p folgendermaßen berechnen: Stab mit V = a 2 l betrachtet A = a 2 , = a + △a 2 ⋅ l + △l − a 2 l alle Glieder, die mehr als ein △ enthalten, werden 2 jetzt vernachlässigt: △l ≪ △l ≪ l : △l + 2la 2 △a = V △l + 2 △a △V = a̸2 l + 2a△al + a 2 △l − a̸2 l = a 2 △l + 2la△a = la 2 ∗ ∗ ∗ a a l l △V ⇒ △V V △l = l 1 2 △a + △al l ⇒ −μ △V = 1 − 2μ V das ist also tatsächliche Volumsänderung eines Körpers bei Dehnung um △l l = Da durch die Dehnung △V > 0 : 1 − 2μ > 0 ⇒ μ < 0.5 Kompression: Tritt statt der Zugspannung ein Druck p auf einen Körper auf, so wird er gestaucht. wirkt z.B. p auf die gegenüberliegenden Seiten A, A’: △l < 0 analog zur Dehnung. Wirkt p auf gesamte Oberfläche des Körpers, ergibt sich ein: △V ∝ p d.h. △VV = −κ ⋅ p V κ ... Kompressibilität, K = κ1 ...Kompressionsmodul Da wir ja aus der Dehnung/Stauchung wissen, wie sich die Längenänderung in jeweils einer Dimension über die Querkontraktion auf die anderen auswirkt, kann der Kompressionsmodul K wieder durch E, μ ausgedrückt werden: Es sei Δx i,k die Längenänderung eines Körpers in Richtung x i durch p auf das Seitenpaar senkrecht zu ⃗e k . Dann ist nach dem Hookeschen Gesetz (∗ mit σ = −p immer Δx i,i = − xEi p und Δx i,k = −μx i Δxk,kk = μx i Ep für i ≠ k Die Längenänderung in einer Richtung hat dann immer drei Anteile: Δx i ges = ∑ 3 i=1 Δx i,k z.B. für x i = x : Δx ges = Δ x,x + Δ x,y + Δ x,z = − Ex p + 2μx Ep = −x Ep 1 − 2μ → Δx x = − Ep 1 − 2μ ∗ ∗ ∗ ∗ Für die gesamte Volumsänderung unter p erhält man dann △V = x + Δxy + Δyz + Δz und daraus wie oben unter Vernachlässigung aller in Δ quadratischen und kubischen Terme: △V = △x + △y + △z = − 3p 1 − 2μ = − 1 p → K = E x z y E V K 31−2μ Veranschaulichung an einem Würfel mit x = y = z = l : V + ΔV = l + Δl 3 = l 3 1 + Δll 3 ≈ l 3 1 + 3 Δll = l 3 + l 3 3 Δll = V − 3V Ep 1 − 2μ mit ∗∗∗∗ V → △VV = 3 Ep 1 − 2μ wie oben und daher wieder K = ΔV E 31−2μ Scherung: Wirkt F tangential auf A = al, so wird h mit einem Winkel α verschoben. F = τ...Schubspannung A Ist α hinreichend klein, gilt τ = G ⋅ α G...Schubmodul, Schermodul Wichtige Anwendung: Torsion eines Drahtes: Drehmoment erforderlich im Gleichgewicht durch elast. Drehmoment kompensiert: ’Torsionswaage’ zur Messung von Drehmomenten (Galvanometer etc.M(I..)) D*(r,L,G)=? bei gegebener Verdrehung ϕ : αr, ϕ, h.. ausgerechnet ⇒ ταr, .. = Gα Grhϕ , dF = τdA = 2rπτdr Gπϕr 2 h −1 dr, dann dM = rdF = 2πGϕ 1h r 3 dr dann M = ergibt: D∗ = M= ∫ r 0 dMr, ..ϕ und Vergleich mit M= D ∗ ϕ... π G R4 2 h πGR ϕ 4 2 h Anmerkung: Alle Formen des Hookeschen Gesetzeshaben die Gestalt: F= A l E△l A F... Ursache ...Geometrie des Körpers l E...Materialkonstante (Modul) △l...Folge