5. Mechanik der deformierbaren Körper (fest, flüssig, gasförmig ) 5.0

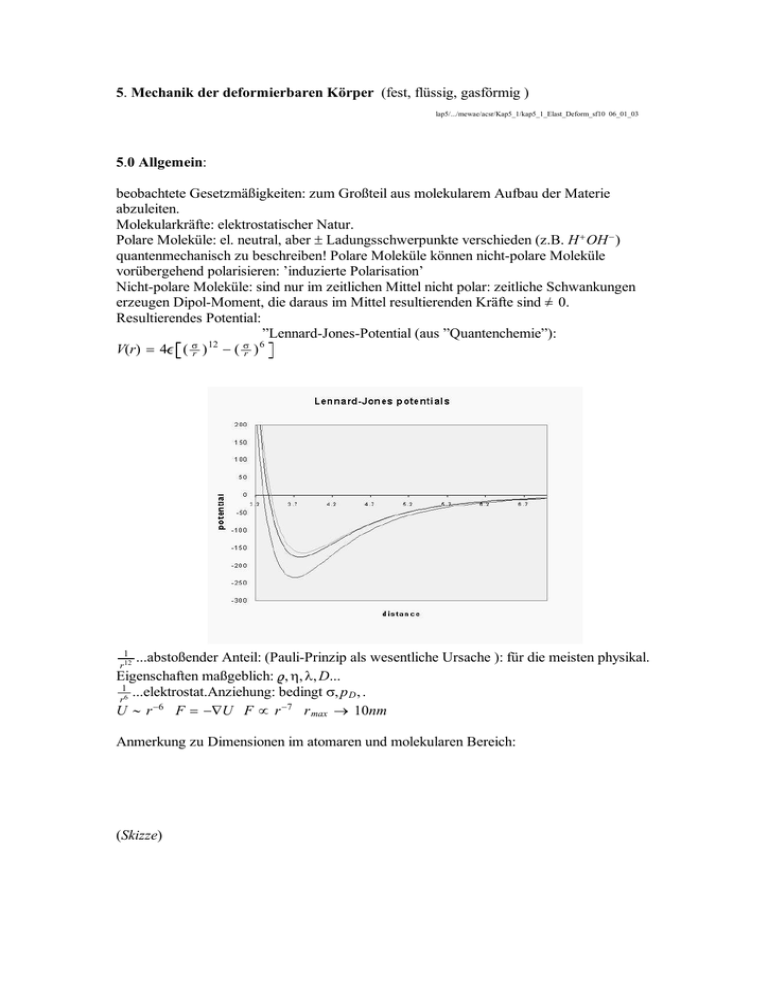
5. Mechanik der deformierbaren Körper (fest, flüssig, gasförmig )
lap5/.../mewae/acsr/Kap5_1/kap5_1_Elast_Deform_sf10 06_01_03
5.0 Allgemein:
beobachtete Gesetzmäßigkeiten: zum Großteil aus molekularem Aufbau der Materie
abzuleiten.
Molekularkräfte: elektrostatischer Natur.
Polare Moleküle: el. neutral, aber ± Ladungsschwerpunkte verschieden (z.B. H + OH − )
quantenmechanisch zu beschreiben! Polare Moleküle können nicht-polare Moleküle
vorübergehend polarisieren: ’induzierte Polarisation’
Nicht-polare Moleküle: sind nur im zeitlichen Mittel nicht polar: zeitliche Schwankungen
erzeugen Dipol-Moment, die daraus im Mittel resultierenden Kräfte sind = 0.
Resultierendes Potential:
”Lennard-Jones-Potential (aus ”Quantenchemie”):
V(r) = 4 ( σr ) 12 − ( σr ) 6
1
r 12
...abstoßender Anteil: (Pauli-Prinzip als wesentliche Ursache ): für die meisten physikal.
Eigenschaften maßgeblich: , η, λ, D...
1
...elektrostat.Anziehung: bedingt σ, p D , .
r6
U ∼ r −6 F = −∇U F ∝ r −7 r max → 10nm
Anmerkung zu Dimensionen im atomaren und molekularen Bereich:
(Skizze)
Festkörper:
geordnete räumliche Struktur (Kristall) ’Fernordnung’: beliebig weit voneinander entfernte
Moleküle haben definierten Abstand voneinander, es gibt ’Gitterkonstante’. Moleküle in
stabiler Lage in Potentialmulden. Temperatur ≡ Schwingung um die Ruhelage: W kin
−W pot .
Festkörper hat definiertes Volumen und definierte Gestalt. Kristall i.a. anisotrop, d.h.
physikalische Eigenschaften sind richtungsabhängig. Amorpher Festkörper: keine
Kristallstruktur, homogen, isotrop. Amorphe Stoffe: oft besonders hart, zäh, µ, λ..
Flüssigkeiten:
höheres W kin der Moleküle, häufiger Platzwechsel mittlerer Abstand ≈ r 0 wie beim
Festkörper, aber Ort der einzelnen Moleküle nicht fix: definiertes Volumen, keine def. Gestalt.
’Nahordnung’: Abstand des nächsten Nachbarn ≈ r 0 aber darüber hinaus nicht mehr scharf
definiert.Übergang amorpher Festkörper - Flüssigkeit ist kontinuierlich, über Zähigkeit und
Elastizitätsmodul (beides kommt noch ) definiert. Da temperaturabhängige Größen: fest
/flüssig: von Temp. abhängig Teer, Glas, Polymere fließen!
Gase:
W kin
−W pot : Moleküle verlassen Potentialtopf: füllen jedes Volumen aus: keine definierbare
Gestalt, kein definiertes Volumen.
5.1 Elastische Deformation fester Körper: und Hooke’sches Gesetz
Deformation:
Gestaltsänderung unter Einwirkung einer Kraft. Elast.Deformation: bei Deformation des
Körpers werden Gegenkräfte wirksam, die nach Aufhören der äußeren, deformierenden Kraft
die Deformationen rückgängig machen. Gesetzmäßigkeit gesucht aus naivem Modell der
Molekularkräfte, die man sich modellhaft als Federn vorstellen kann: Bei Feder: F = −c x
pausibel, wenn ∆x hinreichend klein.
Dabei war c = c(Material, Gestalt) Jetzt soll Abhängigkeit von Material und Gestalt explizit
beschrieben werden.
Gesucht also: f(Material) f(Gestalt)
F∝
l = l = n l
Dehnung: analog zur Feder: F = −c x
F = F 1 = F 2 = F 3 ...F i = c l i = cn l ∝
l aber
l
l
i
i
wenn n Federn hintereinander angeordnet sind
und zusammen um l ausgedehnt werden, so ist die hierfür erforderliche Kraft
F n = 1n F 1 , F 1 = c l ist dabei die erforderliche Kraft, um eine einzelne Feder um l
auszudehnen. F ∝ nl ∝ l l da n mit l anwächst.
Bei nebeneinander angeordneten Federn addiert sich die Kraft:
F = nF 1 wobei jetzt n ∝ A(Querschnitt)
F = const.A
l
l
F=E
A
l
l
Hookes’sches Gesetz:
F = E l (∗)
A
l
σ=E ε
E...Elastitätsmodul
F
= σ...Zugspannung ( mN2 ≡ Pascal, Pa)
A
(Bei einer gegebenen Feder ist A, E udn l konstant:
F = const. l)
(E wäre mit
Atomphysik zu berechnen..)
E ≡ σ das für Verdoppelung von l ( l l = 1, l 2 = l 1 + l = 2l 1 ) erforderlich wäre, wenn der
Körper sich so weit (und nach dem Hookes’schen Gesetz ) dehnen ließe
[E] = [[σ]l ] = [σ] = Pa
l
Einige Zahlenwerte: (ungefähre Angaben )
Material
E
Zugfestigkeit ZF (σ max )
Eisen
100-200 GPa
200 MPa
Stahl
100-200 GPa
2 GPa
Wolfram
400
Beton
40
50 MPa
Nylon
3
300
Holz
ZF
( kPam
)
kg
3
1 − 2.10 −3 ∼ 8.10 3
2.10 −2
250
Bemerkenswert
15
( l maxl )
0.1
140
9.10
−3
Buche ⊥
1.5
7
Holz ist sehr guter Baustoff: Hohe ZF pro Gewicht!
Beispiel:
( l l ) max = σ Emax
z.B. Fe-Draht: A = 1mm 2 :
10 4 Kg
N
E = 100GPa = 10 mN2 = 10 610N
= 10 5 mm
G für
2 ≈
(mm) 2
mm 2
1.5
200
0.7
200
l
l
= 1 für
= 10 −3 , für
l
l
N
2
σ = 100 mm
( l l ) max = 200.10
= 2.10 −3
l = 2mm für l = 1m
2 ≈ 10Kg.g/mm
100.10 9
2
(E wird häufig auch in Kp/mm angegeben: praktische Einheit, 1kp=1Kg.g≈10N)
2
Tragkraft dazu:
F max = σ max A = 2.10 −8 mN2 10 −6 m 2 = 2.10 2 N ≈ 20kg g
Stahl: F max Stahl ≈ 10 F max Fe → l max Stahl ≈ 10
l max Fe
Querkontraktion:
Da bei der Dehnung die Dichte des Körpers (und damit sein Volumen) in grober Näherung
gleich bleibt, erfährt er zugleich eine Querkontraktion, die der Dehnung proportional ist.
a
l (∗ ∗)
a = −µ l
µ..Poissonkoeffizient
Das tatsächlich auftretende V ist also nicht gleich l l , sondern wird durch die
Querkontraktion verringert, man kann es als f(E, p) folgendermaßen berechnen:
Stab mit V = a 2 l betrachtet A = a 2 ,
V = (a + a) 2 (l + l) − a 2 l
alle Glieder, die mehr als ein
jetzt vernachlässigt: l 2
l
l:
V = a 2 l + 2a al + a 2 l − a 2 l = a 2 l + 2la a = la 2 l l + 2la 2 aa = V(
∗ ∗ ∗)
VV
=
ll
(1 +
ε
2
a
a
l
l
)
−µ
enthalten, werden
l
l
+2
a
a
)
(
VV
= ε(1 − 2µ)
das ist also die tatsächliche Volumsänderung eines Körpers bei Dehnung um
µ < 0.5
Da durch die Dehnung V > 0 : 1 − 2µ > 0
l
l
=ε
Kompression:
Tritt statt der Zugspannung ein Druck p auf einen Körper auf, so wird er gestaucht. Wirkt z.B.
p auf die gegenüberliegenden Seiten A, A’: l < 0 analog zur Dehnung. Wirkt p auf gesamte
Oberfläche des Körpers, ergibt sich ein:
V ∝ p d.h.
V = −κ p
V
V
κ ... Kompressibilität, K = κ1 ...Kompressionsmodul
Da wir ja aus der Dehnung/Stauchung wissen, wie sich die Längenänderung in jeweils einer
Dimension über die Querkontraktion auf die anderen Dimensionen auswirkt, kann der
Kompressionsmodul K wieder durch E, µ ausgedrückt werden:
Es sei ∆x i,k die Längenänderung eines Körpers in Richtung x i durch p auf das Seitenpaar
senkrecht zu e k . Dann ist nach dem Hookeschen Gesetz (∗) mit σ = −p immer
∆x i,i = − xEi p
und
∆x i,k = −µx i
∆ k,k
xk
= µx i
p
E
für i ≠ k
Die Längenänderung in einer Richtung hat dann immer drei Anteile:
∆x i ges =
3
i=1
∆x i,k z.B. für x i = x :
∆x ges = ∆ x,x + ∆ x,y + ∆ x,z = − Ex p + 2µx Ep = −x Ep (1 − 2µ) →
∆x
x
= − Ep (1 − 2µ)
(∗ ∗ ∗ ∗)
Für die gesamte Volumsänderung unter p erhält man dann
V = (x + ∆x)(y + ∆y)(z + ∆z) und daraus wie oben unter Vernachlässigung aller in ∆
quadratischen und kubischen Terme:
V
E
= xx + yy + zz = − 3p
(1 − 2µ) = − K1 p → K = 3(1−2µ)
V
E
Veranschaulichung an einem Würfel mit x = y = z = l :
V + ∆V = (l + ∆l) 3 = l 3 (1 + ∆ll ) 3 ≈ l 3 (1 + 3 ∆ll ) = l 3 + l 3 3 ∆ll = V − 3V Ep (1 − 2µ) mit
(∗ ∗ ∗ ∗)
V
→
V
V
= 3 Ep (1 − 2µ) wie oben und daher wieder K =
E
3(1−2µ)
∆V
Scherung:
Wirkt F tangential auf A = al, so wird h um einen Winkel α verschoben.
F
= τ...Schubspannung
A
Ist α hinreichend klein, gilt τ = G α G...Schubmodul, Schermodul
Wichtige Anwendung:
Torsion eines Drahtes: Drehmoment erforderlich, wird im Gleichgewicht durch elast.
Drehmoment kompensiert:
Stellt eine ’Torsionswaage’ zur Messung von Drehmomenten dar
(Galvanometer etc.M(I..))
D ∗ (r, L, G) = ?
bei gegebener Verdrehung ϕ : α(r, ϕ, h..) auszurechnen:
α=
dF =
G
h
rϕ
h
,τ =
ϕ2r 2 πdr
dF
dA
= Gα =
Grϕ
h
, dF =
Gr
h
ϕdA, mit dA = 2rπdr folgt also:
Drehmoment: dM = rdF = 2πGϕ 1h r 3 dr und schließlich M =
4
M = 2πGϕ 1h R4 = π2 G 1h R 4 ϕ
R
0
dM(r, ..ϕ):
Vergleich mit M= D ∗ ϕ... (D ∗ ”Richtmoment”) ergibt:
4
D∗ = π G R
2
h
4
M = πGR ϕ
h
2
Anmerkung: Alle Formen des Hooke´schen Gesetzes haben offenbar die Gestalt:
F = Al E l
A
F... Ursache
...Geometrie des Körpers
l
E...Materialkonstante (Modul)
l...Folge
Analog auch:
Scherung:: τ = 1h G x mit hx = tan α ≈ α
Biegungspfeil ∆s eines einseitig eingespannten Balkens der Länge l: F
etc.
∆s
l3
E
Spannungs-Dehnungs-Diagramm:
Das Hooke’sche Gesetz gilt nur für einen - je nach Material- begrenzten Bereich, dem Bereich
der elastischen Verformung. Darüber dehnt sich das Material plastisch mit
zunehmenderZugkraft bis zur Zugfestigkeit ZF, diese entspricht der maximalen Zugkraft, der
der Körper standhalten kann, bei einer weiteren Dehnung beginnt eine Zerstörung der Struktur,
sodass auch eine abnehmende Kraft zu einer weiteren Dehnung des Körpers möglich ist, bis
der Körper schliesslich zerreißt (Reißfestigkeit RF). Es gibt also für jeden Stoff ein
charakteristisches Verhalten unter einer Zugspannung, das im
Spannungs-Dehnungs-Diagramm dargestellt werden kann.