Mechanik deformierbarer Medien
Werbung

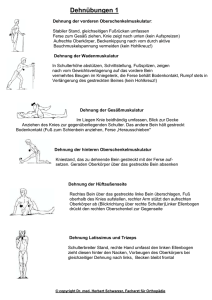
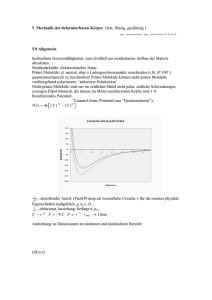
Mechanik deformierbarer Medien Elastomechanik fester Körper, das Hooksche Gesetz Inhalt • Hookesches Gesetz • Elastische und plastische Verformung Vereinfachung des Kraftgesetzes: FederModell für kleine Auslenkungen Resultat: Elastizität F F l l l Dehnungselastizität l / 2 l l / 2 d d d Es ziehe zu beiden Seiten eine Kraft F Dehnung – Hookesches Gesetz Formel E E Δl l F A SI Einheit Anmerkung 1 N / m2 Dehnung 1 N / m2 Elastizitätsmodul Dehnung, relative Längen Änderung 1 1N/ m2 Normalspannung (Kraft / Angriffsfläche) Versuch zum Zusammenhang zwischen atomarem Aufbau und Elastizität • Ausglühen erhöht die Anzahl der Fehlstellen, der Draht wird spröde • „Recken“ ordnet das Gefüge, der Draht wird wieder elastisch Beispiele für Elastizitätsmoduli Formel E l l Einheit Erläuterung N m2 Spannung 1 Dehnung, relative Längenänderung 1 Elastizitätsmodul, Beispiele: Material E N 1 2 m E N/m 2 Fe 2 1011 Al 7 1010 Glas 6 1010 Holz (Esche) 1 1010 Gummi 1 10 9 Die Poisson-Zahl • Wird das Material verlängert, dann wird sein Durchmesser kleiner, weil das Volumen annähernd konstant bleibt. • Das Verhältnis der relativen Änderungen des Durchmessers und der Länge heißt Faktor der Querkontraktion oder PoissonZahl. Sie liegt zwischen 0,2 und 0,5. Die Poisson-Zahl l / 2 l / 2 l d d d Es ziehe zu beiden Seiten eine Kraft d l d l ist die Poisson-Zahl, 0,2 0,5 F Versuch zur Querkontraktion • Querkontraktion eines elastischen Seils Anwendung • Federkraft • Reversible elastische Verformung von festen Stoffen • Gegensatz zu nicht reversibler Verformung – Plastische Verformung, Fließen, Viskosität Dehnung eines Stahldrahts - Hookescher Bereich Spannung Hookescher Bereich Dehnung Dehnung eines Stahldrahts bis zur Bruchgrenze Spannung Hookescher Bereich Dehnung Elastizität Fließen Versuch zum Verlauf der Dehnung • Dehnung eines Stahldrahts bis zum Bruch Zusammenfassung • Die charakteristische Eigenschaft des festen Zustands ist seine Elastizität bei Zugspannung • Hookesches Gesetz im Bereich elastischer Verformung: Die Kraft ist proportional zur Auslenkung – Proportionalitätskonstante: Elastizitätsmodul – Kraft tangential zur Fläche: Scherung, Torsion • Bei zunehmender Belastung: – Fließen – Bruch • Poissonsche Zahl: Beziehung zwischen den unterschiedlichen Modulen Finis