Vorbereitung.Stereometrie

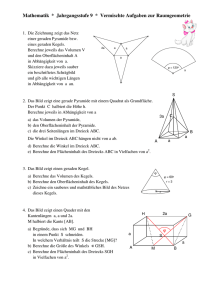
Aufgabe 1
Bei einem geraden Kreiskegel ist die Mantelfläche doppelt so groß wie die Grundfläche.
Wie hoch ist er, wenn das Volumen 100 ist ?
Lösung:
M =π⋅r⋅s
Mantelfläche:
A=π⋅r 2
Grundfläche:
π⋅r⋅s=2 π⋅r 2
s=2 r
h 2=4 r 2 – r 2=3 r 2 ⇒h=√ 3 r
100= 13 π r 2 √ 3 r= √3 r 3
r =3.86497288=3.86
h=6.6943294103=6.69
Aufgabe 2
Eine Kreissektorfläche mit dem Mittelpunktswinkel 135° und dem Radius 8 cm wird zu einem
Kegel zusammen gebogen.
Wie groß ist das Kegelvolumen?
135
135
s=8
Lösung:
2⋅π⋅r = 360⋅π⋅s
r = 360 s=3
2
2
2
2
2
h =s – r =8 – 3 =64−9=55⇒ h=√55
V = 13⋅π⋅32⋅√55=69.89602405387=69.9 cm 3
Aufgabe 3
Eine Pyramide mit quadratischer Grundfläche ABCD und Spitze S hat gleichseitige Dreiecke als
Seitenflächen. In Punkt A sitzt eine Spinne, die zu einer Fliege krabbelt, die in Punkt M in der Mitte
der Strecke CS sitzt.
Wie lang ist die kürzeste Krabbelstrecke?
Lösung:
AB=s
AC =√3⋅s
2
2
2
AM =( ¾ √ 3 s) +( 14 s) =
28
16
AM = 12 √ 7
Aufgabe 4
Ein gerader Kreiskegel hat die Höhe h = 8 cm. Die Abwicklung des Kegelmantels in eine Ebene
ergibt einen Halbkreis.
Berechne Oberflächeninhalt und Volumen des Kegels.
Lösung:
2⋅π⋅r= 12 2 π s ⇒ r= 12 s ⇒ s=2⋅r
h 2=4 r 2 – r 2=3 r 2 ⇒h=r √ 3 ⇒ r=
h
h2
⇒ r 2=
3
√3
1 h2
1
2
1
3
3
V = 3 π⋅r ⋅h= π⋅ ⋅h= 9 π⋅h =178.7217154=178.7 cm
3 3
2
2
2
2
2
A=π⋅r⋅s+π⋅r =2 π r +π⋅r =3 π⋅r =π r =201.061929=201 cm
2
Aufgabe 5
a) Die Mantellinien eines geraden Kreiskegels schliessen mit der Grundfläche des Kegels einen
Winkel von 60° ein. Der Grundkreisradius des Kegels ist 6 cm. Berechne Volumen und Oberfläche
des Kegels.
b) Dem in a) gegebenen Kegel ist ein gerader Kreiskegel so einbeschrieben, dass seine Spitze im
Kreismittelpunkt des gegebenen Kegels liegt. Die Mantellinien des einbeschriebenen Kegels
schließen einen Winkel von 30° ein.
Berechne die Mantelfläche und das Volumen des einbeschriebenen Kegels.
Lösung: nur zu (a)
Seitenansicht ergibt ein gleichseitiges Dreieck
r =6
s=12
h=6 √ 3
V = 13 π 36⋅6 √ 3=72 √ 3 π=391.7806626745=391.8 cm2
A=π⋅r 2+π⋅r⋅s=π 36+π⋅6⋅12=108 π=339.2920065=339.3 cm2
Aufgabe 6
Ein waagerecht im Wasser schwimmender
zylindrischer Baumstamm mit dem Durchmesser
d = 60 cm ragt 15 cm hoch aus dem Wasser.
Welche Dichte hat das Holz ?
Lösung:
F A =F G
F A =ρ fl⋅A fl⋅l⋅g
A fl =
240
π 30 2+15⋅15 √ 3=1884.95559+389.711=2274.666
320
F A =ρ k⋅Ak⋅l⋅g
Ak =π 30 2=2827.43338823=2827.43
ρ fl⋅A fl⋅l⋅g=ρ k⋅Ak⋅l⋅g ⇒ρ k =
A fl
⋅ρ =0.8044985535=0.804 kg / dm3
A k fl
Aufgabe 7
Ein gerader Kreiszylinder hat das Volumen 5,0 cm3 und die Mantelfläche 4.0 cm2.
Berechne die Oberfläche und die Höhe des Zylinders.
A=π⋅r⋅h
Lösung:
V =π⋅r 2⋅h
h=
V
5
=r = =1.25
A
4
A
=1.01859163=1.0186
π⋅r
O=π⋅r 2+π r 2+π⋅r⋅h=π⋅r (2 r +h)=π⋅1.25(2.5+1.019)=13.7519=13.75 cm2
V =π⋅1.252⋅1.019=5.00200455313749=5.002 cm3
Aufgabe 8
Es gilt: a=4 und s=4.5
Berechnen Sie bei der quadratischen Pyramide:
hs, h; Mantelfläche; Volumen ; α , β und
Lösung:
(Kontrolle)
γ
h s= √ 4.52 – 2 2=4.0311288=4.03
h=√ 4.03112 – 22=3,5
1
V = ⋅16⋅3.5=18.666666=18.67
3
A=4⋅12⋅4⋅4.0311=32.2488
cos α=
sinβ=
2 4
= ⇒α=63,61220=63.61°
4.5 9
3.5 7
= ⇒ β=51.057558731=51.06°
4.5 9
tan γ=
3.5 7
= ⇒ γ=60.25511870305=60.26 °
2 4