V20-Kennlinie_der_Va.. - physics (Johannes Dörr)

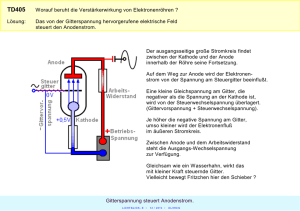
Physikalisches Praktikum
Versuch 20
Kennlinie der Vakuumdiode
Praktikanten:
Johannes Dörr
[email protected]
physik.johannesdoerr.de
Katharina Rabe
[email protected]
1
Gruppe:
14
Datum:
13.02.2007
Assistent:
Sebastian Geburt
Einleitung
Bei einer Vakuum-Diode handelt es sich um ein elektronisches Bauelement und ist heute ein elementarer Bestandteil verschiedenster Geräte, die wir sogar durch die Verwendung im Haushalt in unser alltägliches Leben
involviert haben. Typische Beispiele von Elektrogeräten, in denen diese zumeist als ”Röhren” bezeichneten
Vakuum-Dioden verbaut sind, sind Radios, Fernseher und Oszilloskope. Zumeist wurden sie in der Entwicklung
technischer Geräte durch Transistoren ersetzt, in Geräten mit hoher Leistung findet man sie allerdings immer
noch. Der heutige Versuch wird uns an die Funktionsweise dieser Grundbausteine heranführen, in dem wir die
spezifischen Strom-Spannungs-Kennlinien untersuchen.
2
2.1
Theorie
Aufbau der Vakuum-Diode
Eine Vakuum-Diode besteht aus einem evakuierten Gefäß, oft einer einfache Glasröhre, in die verschiedene
Elektroden, zumeist Anode und Kathode, eingesetzt sind. Die aus einer Metallwendel bestehende Glükathode
wird zur Glühemission gebracht und stößt Elektronen aus. Dieser Effekt wird durch einen Heizstromkreis
1
erreicht. Zu einem Stromfluss innerhalb der Vakuum-Diode kommt es durch eine Beschleunigungsspannung
zwischen Anode und Kathode. Diese sorgt dafür, dass die Elektronen auf dem Weg von der Kathode zur Anode
beschleunigt werden. Zum Stromfluss kommt es daher nur, wenn die Kathode auf einem negativeren Potential
liegt als die Anode. Ist dies nicht der Fall, wird nur ein minimaler Teil des Stroms durchgelassen, da die Diode
dann in Sperrichtung geschaltet ist, ein Effekt, den wir vom Gleichrichter kennen.
2.2
Das Schottky-Langmuir Raumladungsgesetz
Das Raumladungsgesetz geht eigentlich auf die Arbeiten von Clement Child und Irving Langmuir zurück und
wird deshalb auch oft als Langmuir-Child-Raumladungsgesetz bekannt. Durch Walter Schottkys intensive Arbeiten im Bereich der Halbleiterphysik, die ihn letztendlich (und unter Anderem) zur Glühemission (SchottkyEffekt), der Schottky-Diode und der Schottky-Gleichung führte, welche wiederum Langmuirs Arbeit komplettierten, kennt man die daraus resultierende Gleichung als Schottky-Langmuir-Raumladungsgesetz. Dieses Gesetz
beschreibt die Strom-Spannungs-Charakteristik einer Elektronenröhre und besagt, dass die Stromstärke bei
einer idealen Raumladungsvolke innerhalb der evakuierten Röhre mit der 1,5ten Potenz der Anodenspannung
zunimmt, bis zum Punkt der Sättigung, die das Richardsongesetz (siehe unten) beschreibt. Es gilt:
3
I = KU 2 .
(1)
Die Variablen I und U sind hierbei Anodenstrom und Anodenspannung. K ist die Raumladungskonstante der
Diode, (auch Perveanz der Diode) genannt und ist eine Röhrenkonstante, also nur abhängig von der Gestalt
der Elektronenanordnung. Das Raumladungsgesätz gilt bis zur besagten Sättigung, verliert also bei zu hoher
Anodenspannung seine Gültigkeit.
2.3
Der Edison-Richardson-Effekt
Dieser Effekt wurde zunächst von Thomas Edison beobachtet (1883) und beinahe 20 Jahre später (1901) von
Owen Williams Richardson mathematisch erfasst und in die so genannte Richardsongleichung integriert. Er
bezeichnet die thermische Emission von Elektronen aus einer geheizten Kathode im Vakuum. In einem Metall
bewegen sich die Elektronen (in diesem Fall auch als ”Leitungselektronen” bezeichnet) als Elektronengas frei
zwischen den Atomrümpfen. Da die Atomkerne jedoch positiv geladen sind, kommt es zu einer elektrostatischen
Anziehung, die die Elektronen an der Oberfläche am Austritt hindert. Somit ergibt sich für ein bestimmtes
Material eine Austrittsarbeit W , die ein Elektron aufbringen muss, um der Anziehung des Kerns zu entkommen
und das Metall zu verlassen. Diese Austrittsarbeit ist materialspezifisch und liegt je nach Metall bzw. Material
zwischen 1 und 5eV. Durch starke thermische Bewegung der Elektronen, also durch Heizung der entsprechenden Anode, können die Elektronen die Austrittsarbeit aufbringen. Auf Zimmertemperatur ist die thermische
Bewegung der Teilchen, also ihre kinetische Energie, zwar im Durchschnitt um Größenordnungen zu klein, da
die Temperaturverteilung jedoch der Statistik zugrunde liegt, gibt es auch auf Zimmertemperatur immer einige
Elektronen mit ausreichend hoher kinetischer Energie. Die Anzahl n der Teilchen mit genügend kinetischer
Energie 32 kT wächst exponentiell mit der Temperatur T :
W
n ≈ e− kT .
(2)
Die ausgetretenen Elektronen bilden eine Dampfatmosphäre um die Glühkathode. Durch das nun ins Spiel
kommende Richardson-Gesetz können wir die Stromdichte der emittierten Elektronen beschreiben als:
j = CT 2 · e−
W
.
kT
(3)
C wächst mit T und gibt an, wie oft Elektronen auf die Metalloberfläche aufschlagen. Nun wird über die Fläche
der Kathode integriert, was uns zum Strom IS mit angepasstem CK bringt:
W
IS = CK T 2 · e− kT .
2
(4)
Wenn wir beim Sättigungsstrom, der Strom, der aus der geheizten Kathode emittierten Elektronen in den
Anodenstrom umgesetzt wird, so werden die Elektronen von der Anode weggezogen und man kann mit Hilfe
des Stättigungsstroms die Austrittsarbeit W aus der Steigung der Geradengleichung:
ln
W
IS
=−
+ ln CK
T2
kT
(5)
berechnen, die sich ergibt. Da die Boltzmannkonstante bekannt ist, müssen nur I und T gemessen werden.
2.4
Die Kennlinie der Vakuum-Diode
Abbildung 1 im Auswertungsteil zeigt die von uns gemessene Kennlinie der Vakuum-Diode.
2.4.1
Anlaufstrom
Die Elektronen treten zufällig auf die Anode und es entsteht (auch bei nicht angelegter Beschleunigungsspannung) ein ”Anlaufstrom, dessen Kennlinie sich nach dem hochenergetischen Teil der Maxwell-Verteilung verhält:
e|(U )|
,
(6)
I = I0 exp
kB T
die in diesem Bereich annähernd konstant verläuft. Dieser Anlaufstrom ist zunächst abhängig von der Beschaffenheit des Kathodenmaterials. Bei geringer (zu leistender) Austrittsarbeit ist die Anzahl der Elektronen in der
Diode groß, die Stromdichte j ebenso. Dieses Verhalten wird durch die Richardson-Gleichung beschrieben:
−WA
j = AR T 2 exp
,
(7)
kB T
mit der materialspezifischen Richardson-Konstante AR , der Temperatur T , der Boltzmankonstante kB und der
zu leistenden Austrittsarbeit WA .
2.4.2
Raumladungsgebiet
Mit steigender Beschleunigungsspannung verringert sich logischerweise die Zeit, die die Elektronen brauchen,
um von der Kathode zur Anode zu gelangen. Auch die Stromdichte nimmt in diesem Bereich sehr schnell zu.
Allerdings hat die Erhöhung der Beschleunigungsspannung noch einen anderen Effekt, denn gleichzeitig baut
sich um die Anode eine Raumladung auf, es kommen pro Zeiteinheit zu viele Elektronen und die Anode kann
nicht alle aufnehmen. Die entstehende Raumladung wirkt dem Elektronenstrom entgegen, somit verringert
sich der Anstieg des Elektronenstroms mit wachsender Beschleunigungsspannung. Das Schottky-LangmuirRaumladungsgesetz beschreibt diesen Sachverhalt.
4
j = 0
9
r
3
2e (UA − UK ) 2
,
m
l2
(8)
mit der Dielektrizitätskonstante 0 , der Anodenspannung UK , dem Kontaktpotential UK , der Elektronenladung
e, der Elektronenmasse m und der Entfernung zwischen Anode und Kathode l.
2.4.3
Sättigungsbereich
Bei hoher Anodenspannung werden fast alle emittierten Elektronen von der Anode aufgenommen, folglich
nimmt der Strom bei hohen Spannungen nicht mehr zu, sondern strebt gegen einen konstanten Wert. Dies ist
der so genannte Sättigungsbereich der Diode. Je nach Größe der Heizspannung bzw. der Kathodentemperatur
steigt die Anzahl der vorhandenen Elektronen und somit auch der Sättigungsstrom. Zum Erreichen des Sättigungsstroms muss man eine höhere Spannung anlegen, da die Anode eine größere Anzahl von aus der Kathode
austretenden Elektronen absorbieren muss.
3
3
Durchführung
1. Schaltung: Die Röhre GRD7 ist eine Diode, an deren zylindrische Anode sich auf beiden Seiten Schutzringe
anschließen. Diese Schutzringe sollen auf Anodenpotenzial liegen, ohne dass der Strom über sie im Anodenkreis mitgemessen wird.
2. Für drei verschiedene Heizströme 1, 9 ≤ AIH ≤ 2, 1A messe man IA (UA ). IA Anodenstrom, UA Anodenspannung (−10V ≤ UA ≤ 150V ). Im Anlaufstromgebiet kann statt der digitalen Multimeter das
empfindlichere Analog-Messgerät verwendet werden. Messen sie insbesondere den Anlaufstrom (UA = 0V )
und die Spannung UA (IA = 0), bei welcher der Strom verschwindet. Im Raumladungsgebiet sollte die
Schrittweite beim Verändern der Anodenspannung 2V nicht überschreiten. Im Sättigungsbereich kann die
Schrittweite erhöht werden.
3. Für UA = 125V messe man den Sättigungsstrom IS (IH )- in Abhängigkeit vom Heizstrom (1, 8A ≤ IH ≤
2, 15A). Es empfiehlt sich ∆IH = 0, 05A zu wählen.
4. Aus der dem Versuch beiliegenden Eichkurve T (IH ) bestimme man die zu IH gehörende Kathodentemperatur T .
5. Man notiere die Innenwiderstände Ri der verwendeten Instrumente.
4
4.1
Auswertung
Bestimmung des Kontaktpotentials (1. und 2.)
Abbildung 1 zeigt den Anodenstrom in Abhängigkeit von der Anodenspannung.
Kennlinie der Vakuumdiode.
Nach dem Raumladungsgesetz von Schottky-Langmuirsche gilt für die Stromdichte:
r
3
2e
40
(UA − UK ) 2 ,
j= 2
9l
me
Der Verkauf nennt sich
(9)
dabei ist l der Abstand zwischen Kathode und Anode, UA die Anodenspannung, UK die Kontaktspannung, me
die Elektronenmasse und e die Elementarladung. Mit I = j · a, wobei a die Querschnittsfläche ist, die der Strom
durchtritt, ergibt sich:
r
3
4 a 0
2e
I =
(UA − UK ) 2
(10)
a l2
me
|
{z
}
c1
I
2
2
3
2
3
= c1 (UA − UK ) = m UA + b
(11)
2
mit b = −UK · c13 = −UK m. In Abbildung 2 ist I 3 in Abhängigkeit von UA innerhalt des Raumladungsgebiets
aufgetragen. Aus der linearen Regression erhalten wir die Steigung m und den Y-Achsenabschnitt b. Für die
Kontaktspannung UK gilt nun:
UK = −
b
,
m
und wir erhalten damit aus den drei Messungen die folgenden Werte für UK :
UK (IH = 1,9A) = −2,02(6)V
UK (IH = 2,01A) = −1,82(6)V
UK (IH = 2,1A) = −1,53(5)V
4
(12)
Figure 1: Anodenstrom in Abhängigkeit in Abhängigkeit von der Anodenspannung
5
Figure 2: Dritte Wurzel des Quadrats des Anodenstroms in Abhängigkeit von der Anodenspannung innerhalb
des Raumladungsgebiets
6
Figure 3: ln(UA − UK ) in Abhängigkeit von ln(IA )
Der Fehler ergibt sich aus:
s
σUK =
4.2
1
σb
m
2
+
b
σm
m2
2
.
(13)
Berechnung des Exponenten im Raumladungsgesetz (3.)
Wir verwenden (10) und formen um:
3
= c1 (UA − UK ) 2
3
ln(I) = ln(c1 ) + ln(UA − UK ) .
2
I
(14)
(15)
In Abbildung 3 ist ln(UA − UK ) in Abhängigkeit von ln(I) aufgetragen. Die Steigung der Regressionsgeraden
sollte hiernach 3/2 betragen. Der Mittelwert unserer drei Ergebnisse beträgt 1, 54(1) und hat davon eine
Abweichung von 3%.
7
Figure 4: 1/T in Abhängigkeit von ln(IS /T 2 )
8
4.3
Austrittsarbeit und Richardson-Gesetz (4.)
Um die benötigte Fläche und die Austrittsarbeit zu bestimmen, verwenden wir die Richardson-Gleichung:
I
WA
B T
−k
= Ar a T e
| {z }
(16)
c2
⇒ ln
I
T2
ln(c2 ) −
=
WA
.
kB T
(17)
Die materialspezifische Richardsonkonstante beträgt für Wolfram Ar = 72 AK −2 cm−2 . Abbildung 4 zeigt
ln( TI2 ) in Abhängigkeit von T1 und aus der Regression erhalten wir die Steigung m und den Y-Achsenabschnitt
b.
WA
⇒ WA = −m kB
kB
eb
b = ln(Ar a) ⇒ a =
.
Ar
m
=
−
(18)
(19)
Die Temperatur wurde nicht direkt gemessen sondern mit der Formel
T (IH ) = 579
K
· IH + 1150,2K
A
(20)
berechnet.
Wir erhalten die Werte:
WA = 5,28(9) eV
a = 1,17(48) cm2
Für die Austrittsarbeit WA ergibt sich im Vergleich zu den im Praktikumsskript angegebenen Wert eine Abweichung von 17%.
4.4
Abschätzung der Fehler für IA und UA (5.)
Die Innenwiderstand des Ampèremeters des Anodenstroms ist mit 10Ω vernachlässigbar klein, der in Reihe
geschaltete Widerstand (2,2KΩ) ist um einige Größenordnungen größer. Der Innenwiderstand des Voltmeters
für die Spannung UA ist sehr groß, und somit ebenfalls zu vernachlässigen, da der meiste Strom über den
parallelgeschalteten Widerstand (600Ω) fließt.
5
Diskussion
Die Endergebnisse unseres Versuchs sind im Grunde genommen zufrieden stellend. Zwar erreichten wir bei der
Errechnung der Austrittsarbeit WA eine Abweichung von 17 % gegenüber dem im Skript angegebenen Wert,
allerdings erhielten wir an anderer Stelle schöne Schaubilder für die Kennlinie unserer Diode und im Großen und
Ganzen konnten unsere Ergebnisse somit mit den Erwartungen an den Versuch mithalten. Warum es dennoch
zu einer starken Abweichung bei der Austrittsarbeit kam, ist schwer zu sagen, da gerade in diesem Versuch
beispielsweise die Innenwiderstände der verwendeten Amperemeter vernachlässigbar klein sind, was wiederum
daran liegt, dass sie mit wesentlich größeren Widerständen in Reihe geschaltet sind. Es fiel uns schwer, hier
einen eindeutigen Grund für die Abweichung zu finden, auch haben wir erfahren, dass vorherige Jahrgänge sehr
oft den gleichen Fehler erhielten und diesen ebenfalls nicht erklären konnten. Insofern belassen wir es an dieser
Stelle bei einem angenehm abgelaufenen Versuch und einer Auswertung, die zumindest zur Hälften unseren
Anforderungen an das Ergebnis gerecht wurde.
9