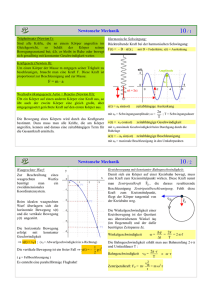
mv F rm 4 r F mr T ⋅ = ⋅ π ⋅ = ⋅ω

Kontrolle Physik-Leistungskurs Klasse 11
2.12.2014
Drehbewegung, Radialkraft
1. Die Zeiger der Rathausuhr haben vom
Drehpunkt aus gemessen eine Länge von
820 mm und 550 mm. Sie werden durch
das Uhrwerk gleichförmig bewegt.
Mit welchen Geschwindigkeiten bewegen
sich die am weitest außen liegenden
Punkte der beiden Zeigers? (4)
2. Vater und Sohn sind mit dem Rad
unterwegs, der eine mit einem 28er, der
andere mit einem 22er Rad. Als es
dunkel wird, schalten beide ihre Lampen
an, indem sie ihren Dynamo an das
Vorderrad andrücken. Wie verhalten sich
die Helligkeiten der Lampen zueinander,
wenn beide gleich schnell fahren und
identische Lichtanlagen haben? (1)
a) Das Licht an dem großen Rad ist
heller.
b) Das Licht an dem kleinen Rad ist
heller.
c) Die Lichter sind gleich hell.
3. Ein Käfer (m=1g) rotiert windgeschützt auf der Flügelspitze (r=15m) einer
Windkraftanlage, die für eine Umdrehung 4 s braucht. Mit welcher Kraft muss sich der Käfer
mit seinen kleinen Käferbeinen an dem Flügel festhalten, damit er darauf sitzen bleibt? (4)
4. Die beiden Gleichungen beschreiben die Größe der Radialkraft in Abhängigkeit von den
Bahnparametern einer gleichförmigen Kreisbewegung.
FR =
m⋅ v2
r
m ⋅ 4 π2 ⋅ r
FR = m ⋅ω ⋅ r =
T2
2
Geben sie für die unten beschriebenen Fälle an, wie sich die Größe der Radialkraft
verändern muss, wenn sich der entsprechende Bahnparameter ändert. (4)
a) Bei konstanter Masse und konstantem Bahnradius wird die Bahngeschwindigkeit
vervierfacht.
b) Bei konstanter masse und konstanter Bahngeschwindigkeit wird der Bahnradius
verdoppelt.
c) Bei konstanter Masse und konstanter Umlaufzeit wird der Bahnradius verdoppelt.
d) Bei konstantem Bahnradius werden Masse und Umlaufzeit halbiert.
Lösungen
1. Die Umlaufzeit des Minutenzeigers beträgt 60 min oder 3600 s.
Mit der Gleichung für die Bahngeschwindigkeit
v = ω⋅ r
2 π⋅ r
T
kann die Geschwindigkeit berechnet werden:
2 π⋅ 820mm
v=
3600 s
v=
mm
s
Der Stundenzeiger braucht für eine Umdrehung 12 Stunden oder 43 200 s. Damit erhält man
für ihn eine Geschwindigkeit von 0,08 mm/s.
v = 1,4
2. Lösung: c ist richtig, beide Lampen sind gleich hell.
Da beide mit gleicher Geschwindigkeit fahren, ist die Bahngeschwindigkeit eines Punktes auf
dem Reifen gleich groß. Damit drehen sich auch die Dynamos gleich schnell und liefern
gleiche Spannungen.
Dass das kleine Rad sich öfter drehen muss, spielt dabei keine Rolle.
3.
geg.:
m = 1⋅10 −3 kg
ges.:
F
r = 15m
T=4s
Lösung:
Damit der Käfer die Kreisbewegung mitmachen kann, muss er sich
mit der dazu notwendigen Radialkraft an der Flügelspitze festkrallen.
m⋅ v 2
F=
r
Über die Geschwindigkeit ist noch nichts bekannt. Die Bewegung ist
aber gleichförmig und Weg und Zeit sind bekannt. Der in 2 s
zurückgelegte Weg ist der Umfang des gesamten Windrades:
s
t
2⋅ π ⋅r
v=
T
v=
Damit erhält man die Radialkraft:
m ⋅ 4 ⋅ π2 ⋅ r 2
F=
r ⋅T
F=
m ⋅ 4 ⋅ π2 ⋅ r
T
1 ⋅10−3 kg ⋅ 4 ⋅ π2 ⋅15m
4 2 s2
F = 0,037N
F=
Antwort:
Damit muss der Käfer eine Kraft aufbringen, die nicht ganz dem
Vierfachem seines Körpergewichtes entspricht.
Der Käfer muss sich mit 0,037 N festhalten.
4. Für jeden einzelnen Fall muss entschieden werden, welche der beiden Formeln zutrifft.
a) Den Zusammenhang zwischen Radialkraft und Bahngeschwindigkeit beschreibt die erste
Formel. Sind die Masse und der Bahnradius konstant, gilt
FR v 2
Wird die Bahngeschwindigkeit vervierfacht, muss sich die Radialkraft um das Sechzehnfache
erhöhen, um den Körper noch auf dieser Bahn zu halten.
b) Auch hier kann die erste Formel verwendet werden. Bei konstanter Masse und
Bahngeschwindigkeit gilt
1
FR
r
Wird der Radius verdoppelt, ist nur noch die halbe Radialkraft notwendig, um den Körper auf
der Bahn zu halten.
c) Es wird jetzt die zweite Formel verwendet. Da Masse und Umlaufzeit konstant sind, gilt
FR r
Eine Verdopplung des Bahnradius bedeutet also eine Verdopplung der notwendigen
Radialkraft.
Das widerspricht auf den ersten Blick der Aussage von Aufgabe b. Wenn die Umlaufzeit aber
konstant bleibt, muss sich die Bahngeschwindigkeit vergrößert werden.
d) Für die letzte Aufgabe kommt wieder die zweite Formel zum Einsatz. Es bleibt nur der
Bahnradius konstant, also gilt
m
FR 2
T
Eine Halbierung der Masse bringt eine Halbierung der Radialkraft mit sich. Durch die
Halbierung der Umlaufzeit wird die Kreisbewegung aber deutlich schneller, was auf Grund
des Quadrates eine Vervierfachung der Radialkraft bewirkt.
Damit muss im Endeffekt die Radialkraft verdoppelt werden.