Formelsammlung Physik

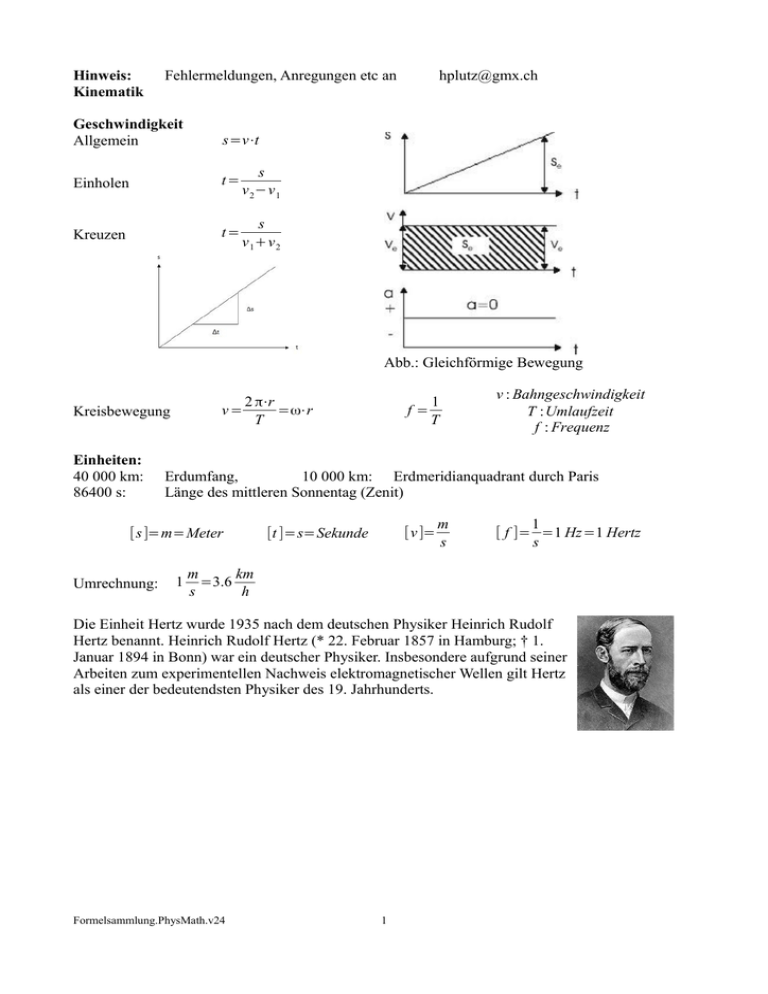
Hinweis:
Kinematik
Fehlermeldungen, Anregungen etc an
Geschwindigkeit
Allgemein
s=v⋅t
Einholen
t=
s
v 2−v 1
Kreuzen
t=
s
v 1+v 2
[email protected]
Abb.: Gleichförmige Bewegung
v=
Kreisbewegung
Einheiten:
40 000 km:
86400 s:
2 π⋅r
=ω⋅r
T
1
T
v : Bahngeschwindigkeit
T :Umlaufzeit
f : Frequenz
Erdumfang,
10 000 km: Erdmeridianquadrant durch Paris
Länge des mittleren Sonnentag (Zenit)
[s ]=m=Meter
Umrechnung:
f=
1
[v ]=
[t ]=s=Sekunde
m
s
1
[ f ]= =1 Hz=1 Hertz
s
m
km
=3.6
s
h
Die Einheit Hertz wurde 1935 nach dem deutschen Physiker Heinrich Rudolf
Hertz benannt. Heinrich Rudolf Hertz (* 22. Februar 1857 in Hamburg; † 1.
Januar 1894 in Bonn) war ein deutscher Physiker. Insbesondere aufgrund seiner
Arbeiten zum experimentellen Nachweis elektromagnetischer Wellen gilt Hertz
als einer der bedeutendsten Physiker des 19. Jahrhunderts.
Formelsammlung.PhysMath.v24
1
Beschleunigung
Gleichmässige Beschleunigung ohne Anfangsgeschwindigkeit
v=a · t
v 2 =2 a · s
s= 12 v⋅t
1
s= 2 a⋅t
Einheiten:
2
m
[v ] s m
[a]= = = 2
[t ] s s
Gleichmässige Beschleunigung mit Anfangsgeschwindigkeit v0:
2
v =v 0+a · t
Fallbeschleunigung:
Ort
Pol
9.83219 m/s2
g
v= g · t
v 2 =2 g · h
1 2
s=v 0⋅t+ a⋅t
2
2
v =v 0+2⋅a · s
45
Äquator
Zürich
9.80620 m/s2
9.78033 m/s2
9,806800 m/s2 1,62 m/s2
1
s= v⋅t
2
Mond
1
h= g⋅t 2
2
Schwere- und Gravitationsbeschleunigung ausgewählter Himmelskörper.
Die Tabelle enthält die Gravitations-, die Zentrifugal- und die resultierende Schwerebeschleunigung
der acht Planeten unseres Sonnensystems und des Mondes. Die Werte gelten für die Oberfläche am
Äquator und sind in m/s2. Das negative Vorzeichen der Zentrifugalbeschleunigung soll
verdeutlichen, dass diese der Gravitationsbeschleunigung entgegengerichtet ist.
Formelsammlung.PhysMath.v24
2
Himmelskörper
Gravitationsbeschl Schwerebeschleun Zentrifugalbeschle
eunigung
igung
unigung
1
Merkur
3,70
3,70
−3,75·10–6
2
Venus
8,87
8,87
−5,41·10–7
3
Erde
9,798
9,780
−0,0339
Mond
1,62
1,62
−1,23·10–5
4
Mars
3,71
3,69
−0,0171
5
Jupiter
24,79
23,12
−2,21
6
Saturn
10,44
8,96
−1,67
7
Uranus
8,87
8,69
−0,262
8
Neptun
11,15
11,00
−0,291
Horizontaler Wurf
Unter dem waagerechten(auch waagrechten) beziehungsweise horizontalen Wurf versteht man in
der Physik den Bewegungsvorgang, den ein Körper vollzieht, wenn er parallel zum Horizont
geworfen wird, sich also mit einer horizontalen Startgeschwindigkeit nur unter dem Einfluss seiner
Gewichtskraft bewegt. Die resultierende Bahnkurve ist eine Wurfparabel mit dem Abwurfort als
Scheitel.
Der waagrechte Wurf lässt sich nach dem Superpositionsprinzip(Unabhängigkeitsprinzip) in zwei
Teilbewegungen zerlegen, die Bewegung in x-Richtung und in y-Richtung beeinflussen sich
gegenseitig nicht. Dies funktioniert aber nur dann, wenn man den Wurf unter idealisierten
Bedingungen, also etwa ohne Berücksichtigung des Luftwiderstandes betrachtet.
√
2 h0
g
Wurfdauer:
t=
Wurfweite:
W =v 0⋅t=v 0⋅
√
2 h0
g
Schiefer Wurf
Die Wurfparabel ist die Flugbahn, die ein Körper beim Wurf in einem homogenen Schwerefeld
beschreibt, wenn man den Einfluss des Luftwiderstands vernachlässigt. Der schiefe Wurf stellt
dabei den Regelfall dar – senkrechter und waagerechter Wurf sind Ausnahmefälle. Der Scheitel der
Parabel befindet sich dabei am höchsten Punkt der Flugbahn, die Parabel ist nach unten geöffnet.
Die ballistische Kurve ist die von der idealen Wurfparabel abweichende Kurve unter Einfluss des
Luftwiderstandes. Die Wurfparabel ist die Idealisierung der ballistischen Flugbahn.
Formelsammlung.PhysMath.v24
3
Reichweite
Die Reichweite R wird üblicherweise dadurch definiert, dass die Wurfparabel die Ausgangshöhe
wieder erreicht, d.h.:y(R)= 0. Damit kann man die Bewegungsgleichung nach R auflösen und
v2
erhält: R= 0⋅sin( 2β)
g
Mathematische Beschreibung
Der Körper wird mit einer Geschwindigkeit v0 unter dem Winkel β schräg nach oben geworfen.
Dann gilt für die Geschwindigkeitskomponenten, aus denen die Abwurfgeschwindigkeit durch
lineare Superposition zusammengesetzt ist (unter Vernachlässigung des Luftwiderstands):
•horizontal: horizontale Komponente der Anfangsgeschwindigkeit: x (t)=v 0⋅t⋅cos β
•vertikal: vertikale Komponente der Anfangsgeschwindigkeit plus Geschwindigkeitsänderung durch
g 2
konstante Beschleunigung: y (t)=v 0⋅t⋅sin β – ⋅t
2
Startwinkel für die maximale Reichweite:
Da die Sinusfunktion bei 90 °ihren grössten Wert sin 90° = 1 hat, erreicht man bei Anfangshöhe h0 =
0 die grösste Reichweite für βmax =45 ° .
Wurfparabel (Springbrunnen im Garten des
Schloss Belvedere, Wien, Österreich).
Formelsammlung.PhysMath.v24
Beispiel zur oberen (blau; 71,1°) und unteren
(orange; 18,9°) Winkelgruppe. Beide
Wurfparabeln führen bei gleicher
Anfangsgeschwindigkeit zum Ziel in 100 m
Entfernung.
4
Zentripetalbeschleunigung
Zentripetalbeschleunigung:
a=
v2
r
m 2
)
2
[v ]2
s
m
m
[a]=
=
= 2 = 2
[r]
m
s ⋅m s
(
Keplersche Gesetze
Johannes Kepler (lateinisch Ioannes Keplerus, auch Keppler; * 27. Dezember
1571 in Weil der Stadt; † 15. November 1630 in Regensburg) war ein deutscher
Naturphilosoph, Mathematiker, Astronom, Astrologe, Optiker und
evangelischer Theologe.
In seiner Laufbahn war Kepler Mathematiklehrer an der protestantischen
Stiftsschule in Graz. Ihr gegenüber stand die katholische Universität von Graz.
Kepler war in Prag Assistent von Tycho Brahe, Kaiserlicher Mathematiker bis
zu seinem Tod, zunächst unter Rudolf II., dann unter dessen Nachfolger
Landesmathematiker in Linz und Hofastrologe von General Wallenstein.
Grafische Zusammenfassung der drei Keplergesetze:
1. Gesetz
1609
Zwei ellipsenförmige Umlaufbahnen, Brennpunkte
F1 und F2 für den Planet 1, F1 und F3 für den Planet
2, die Sonne (sun) in F1; grosse Halbachsen a1 und
a2.
2. Gesetz
1609
Die beiden grauen Sektoren A1 und A2, die in
derselben Zeit überstrichen werden, haben dieselbe
Fläche.
3. Gesetz
1616
Die Gesamtumlaufzeiten der Planeten 1 und 2
verhalten sich wie
a13/ 2 T 1
=
a 3/2 2 T 2
oder
a3
=const
T2
Ellipse
Eine Ellipse kann definiert werden als die Menge aller Punkte P der Ebene, für die die Summe der
Abstände zu zwei gegebenen Punkten F1 und F2 gleich ist. Die Punkte F1 und F2 heissen
Brennpunkte.
E={P∣PF 1+ F 2 P=const } oder
Formelsammlung.PhysMath.v24
d 1+d 2=2 a
5
F 1 D=F 2 D=a
e, c:
Lineare Exzentrizität
e 2+b 2=a 2 oder c 2+b 2=a 2
ε:
numerische Exzentrizität
e
ϵ= <1
a
also: e=a⋅ϵ
Dichte
m
V
Dichte:
ρ=
Einheiten:
[ρ]=
ρ: rho
[m] kg
=
[V ] m3
Umrechnung: 1
g
kg
kg
=1
=1000 3
3
3
cm
dm
m
1 kg : Masse von einem Kubikdezimeter Wasser bei vier Grad Celsius
Tabelle
Material
Dichte
Alkohol
Wasser
Aluminium
0,79 g/cm3
(20 °C)
0,998 g/cm3 2,7 g/cm3
(20 °C)
Eisen
m
[ F ]=[m]⋅[a]=kg⋅ 2 = N =Newton
s
Gravitationskraft
Formelsammlung.PhysMath.v24
6
Gold
7,874 g/cm3 11,342 g/cm3 19,32 g/cm3
(20 °C)
(20 °C)
Dynamik
F =m⋅a
Blei
m⋅M
F Gravitation =G⋅ 2
r
2
m
2
kg
(Gravitationskonstante)
G=6.6710−11 N
24
Masse der Erde:
m Erde=5.979⋅10 kg
Masse des Mondes:
m Mond =7.357⋅10 kg
Radius der Erde:
R Erde=6.3713⋅10 6 m
Masse der Sonne:
22
Mittelpunktabstand Erde – Sonne: r Erde− Sonne =1.4957⋅1011 m
Mittelpunktabstand Erde – Mond: r Erde− Mond =3.84403⋅108 m
Gewichtskraft
Gewichtskraft
F G=m⋅g
Schiefe Ebene
Gewichtskraft
F G=m⋅g
Normalkraft
F N = F G⋅cos( α)
Hangabtriebskraft
F H =F G⋅sin (α)
Reibungskraft
F R=μ⋅F G⋅cos (α)
tg α=µ → α=arc tg (µ)
Formelsammlung.PhysMath.v24
7
30
mSonne =1.991⋅10 kg
Luftwiderstand
Laminare Strömung
Bei laminarer Strömung wird der Strömungswiderstand nur durch die innere Reibung des Mediums
verursacht. Ist η die dynamische Viskosität des Mediums, so gilt für kugelförmige Körper vom
Radius r das Stokessche Gesetz
F W =6 π⋅η⋅v⋅r
Turbulente Strömung
In einer turbulenten Strömung lässt sich der Strömungswiderstand nur durch Experimente
bestimmen, bzw. durch komplizierte numerische Rechnung, z. B. mittels Finite-Element-Methoden,
annähern.
Bei Kraftfahrzeugen kann im relevanten Geschwindigkeitsbereich von turbulenter Strömung
ausgegangen werden. Im modernen Automobilbau ist der cW–Wert, der Luftwiderstandsbeiwert, von
grosser Bedeutung. Er kann im optimalen Falle 0,09 betragen, bei einem Omnibus steigt er bis auf
0,6.
1
F W =cW⋅A⋅2⋅ρ⋅v
2
Federgesetze
Federkraft
F =D⋅s
Umrechnung
[ D]=
1
[F ] N
=
[s ] m
N
N
=100
cm
m
D: Deformationskonstante
f, k: Federkonstante, fast gleiche Bedeutung
Formelsammlung.PhysMath.v24
8
Hydrostatik
Die Dichte ρ (Rho), auch Massendichte genannt, ist der Quotient aus der Masse m eines
m
Körpers und seinem Volumen V : ρ=
V
Sie wird meist in Gramm pro Kubikzentimeter angegeben, bei flüssigen Körpern ist auch die
Einheit Kilogramm pro Liter üblich. Die Dichte ist durch das Material des Körpers bestimmt und
als intensive Grösse von seiner Form und Grösse unabhängig.
Im Allgemeinen dehnen sich Stoffe mit steigender Temperatur aus, wodurch ihre Dichte sinkt. Eine
Ausnahme bilden Stoffe mit einer Dichteanomalie wie z. B. Wasser.
m
V
Dichte
ρ=
Druck
p=
Schweredruck
p=ρ⋅g⋅h
F
A
[ρ ]=
[ m] kg
=
[V ] m 3
[ p]=
1 g / cm3 =1 kg / dm3=1000 kg / m3
[F ] N
= =1 Pa=1 Pascal
[ A] m 2
Hydraulische Presse
p=
F1 F 2
=
A1 A2
Blaise Pascal (* 19. Juni 1623 in Clermont-Ferrand; † 19. August 1662 in Paris)
war ein französischer Mathematiker, Physiker, Literat und katholischer Philosoph
Auftrieb
F A=ρ⋅V⋅g
Die Auftriebskraft eines Körpers in einem Medium ist genauso
gross wie die Gewichtskraft des vom Körper verdrängten
Mediums. F1 und F2 sind die Druckkräfte der Flüssigkeit auf den
Körper.
Beweis:
Kraft nach oben
F 2= A⋅p 2 = A⋅ρ⋅g⋅h2
Kraft nach unten
F 1= A⋅p 1= A⋅ρ⋅g⋅h1
resultierende Kraft nach oben
Δ F = F 2 − F 1 = A⋅ρ⋅g⋅(h 2−h 1)=ρ⋅V⋅g=m⋅g
Formelsammlung.PhysMath.v24
9
Archimedes (griechisch ᾿Αρχιμήδης) von Syrakus (* um 287 v. Chr.
vermutlich in Syrakus auf Sizilien; † 212 v. Chr. ebenda) war ein antiker
griechischer Mathematiker, Physiker und Ingenieur. Er gilt als einer der
bedeutendsten Mathematiker der Antike. Seine Werke waren auch noch im 16.
und 17. Jahrhundert bei der Entwicklung der höheren Analysis von Bedeutung.
Hydrodynamik
Daniel Bernoulli (* 29. Januarjul./ 8. Februar 1700greg. in Groningen;
† 17. März 1782 in Basel) war ein Schweizer Mathematiker und
Physiker aus der Gelehrtenfamilie Bernoulli. Er arbeitete mit
Leonhard Euler an den Gleichungen, die ihre Namen tragen. Der
Bernoulli-Effekt ist von überragender Bedeutung in der Aerodynamik.
Energiesatz, Bernoulli
1
p⋅V +m⋅g⋅h+ ⋅m⋅v 2=const
2
1
p+ρ⋅g⋅h+ ⋅ρ⋅v 2=const
2
Beweis:
A⋅v=const
W =W Lage+W Bewegung +W Druck
Arbeit, Energie und Leistung
Arbeit:
W =F⋅s
Hubarbeit, Lageenergie, Potenzielle Energie
W =m⋅g⋅h
Beschleunigungsarbeit, Bewegungsenergie, Kinetische Energie
1
W = 2⋅m⋅v
2
Federarbeit, Spannenergie
W = 12⋅D⋅s 2=
F 1 +F 2
⋅s
2
Formelsammlung.PhysMath.v24
10
Energie:
Energie ist gespeicherte Arbeit
Leistung:
W =P⋅t
P=F⋅v
Einheiten (mkgs-System)
[t ]=s=Sekunde
[s ]=m=Meter
m
[ F ]=[m]⋅[a]=kg⋅ 2 = N =Newton
s
Sir Isaac Newton [ˌaɪzək ˈnjuːtən] (* 25. Dezember 1642jul./ 4. Januar
1643greg. in Woolsthorpe-by-Colsterworth in Lincolnshire; † 20. März
1726jul./ 31. März 1727greg. in Kensington) war ein englischer Naturforscher
und Verwaltungsbeamter. In der Sprache seiner Zeit, die zwischen natürlicher
Theologie, Naturwissenschaften und Philosophie noch nicht scharf trennte,
wurde Newton als Philosoph bezeichnet.
[W ]=[ F ]⋅[s ]=N⋅m=J = Joule=W⋅s
Physik
J
[W ]=[ P ]⋅[t ]=kWh=1000 ⋅3600 s=3 600 000 J =3.6 MJ
s
1 kWh=3.6 MJ
Industrie
James Prescott Joule (* 24. Dezember 1818 in Salford bei Manchester; † 11.
Oktober 1889 in Sale (Greater Manchester), Aussprache: dʒuːl) war ein
britischer Physiker. Joule war der dritte Sohn eines Brauereibesitzers. Später
übernahm und betrieb er diese Brauerei zusammen mit seinem Bruder.
[ P]=
[W ] J
= =W =Watt
[t]
s
James Watt (* 19. Januarjul./ 30. Januar 1736greg. in Greenock; † 25. August
1819[1] in seinem Haus in Heathfield, Staffordshire) war ein schottischer
Erfinder. Seine, aus heutiger Sicht, einflussreichste Erfindung war die
Verbesserung des Wirkungsgrades von Dampfmaschinen durch Verlagerung
des Kondensationsprozesses aus dem Zylinder in einen separaten
Kondensator.
Formelsammlung.PhysMath.v24
11
Pferdestärke (75 kg 1 m in einer Sekunde)
1 kW =1.3596PS = 1.36 PS
1 PS = 735,498 75 W = 736 W
Kalorik
Δ l=l 0⋅α⋅Δ ϑ
Δ ϑ:Temperaturänderung in ° C
l=l 0⋅(1+α⋅Δ ϑ)
Material Eisen
α
12,2·10-6
Aluminium
1
°C
*
23,2·10-6
Kupfer
1
°C
16,5·10-6
Messing
1
°C
18,4·10-6
Zink
1
°C
26,3·10-6
1
°C
V =V 0⋅γ⋅Δ ϑ
•
•
Eisen
11.8; 11.7
X12CrNi188 16
Material Wasser 20°
γ
0.21 10-3
Grauguss
Ethanol
1
°C
1,10 10-3
9.0
Stahl C 15
Benzin
1
°C
1.06 10-3
11.1
Quecksilber
1
°C
0,182 10-3
Glyzerin
1
°C
0.5 10-3
1
°C
γ=3 α
[c]= kg⋅°J C
Δ W =m · c · Δ ϑ
Material
Wasser
Spez.
Wärmekapazität c
4180
J
kg⋅° C
Wasser
fest
Wasser
flüssig
Wasser
gasförmig
Δ W = L· Δ m
c : spezifische Wärmekapazität
Aluminium Eisen
896
J
kg⋅° C
439
Kupfer
J
kg⋅° C
Wassereis
Wasserdampf
381
Silber
J
kg⋅° C
c = 2100
J
kg⋅° C
c = 4180
J
kg⋅° C
c = 1600
J
kg⋅° C
237
Blei
129
J
kg⋅° C
L: spezifische Schmelzwärme, spezifische Verdampfungswärme
kJ
Die spezifische Schmelzenergie von Blei beträgt
Die Schmelztemperatur von Blei beträgt
L = 23· kg
ϑ = 327 °C
Die spezifische Schmelzwärme von Wasser beträgt
Lf = 335
kJ
kg
Die spezifische Verdampfungswärme von Wasser beträgt Lv = 2258·
Formelsammlung.PhysMath.v24
J
kg⋅° C
12
kJ
kg
Einheiten
[c]= kg⋅°J C
[α]= °1C
Gasgesetze
p⋅V =n⋅R⋅T = N⋅k⋅T
p⋅V =const
V
=const
T
Gesetz von Boyle-Mariotte
Iren Robert Boyle (1662) und dem Franzosen Edme Mariotte (1676)
Gesetz von Gay-Lussac
1787 von Jacques Charles und 1802 von Joseph Louis Gay-Lussac
p
=const
T
Gesetz von Amontons
Wellen und Schwingungen
Achtung Definition cis
t
x (t )=x 0⋅sin (2 π⋅ )
T
t
x
y (t)= x 0⋅sin(2 π⋅ −2 π⋅ )
λ
T
Als Fourierreihe (nach Jean Baptiste Joseph Fourier) einer periodischen Funktion f, die
abschnittsweise stetig ist, bezeichnet man deren Entwicklung in eine Funktionenreihe aus Sinusund Kosinusfunktionen.
Die Basisfunktionen der Fourierreihe bilden ein bekanntes Beispiel für eine Orthonormalbasis. Im
Rahmen der Theorie der Hilberträume werden auch Entwicklungen nach einem beliebigen
vollständigen Orthonormalsystem als Fourierreihe bezeichnet
Dreiecksfunktion:
f (t)=−
f (t)=
8h
1
⋅[cos( ω⋅t)+ 2⋅cos (3⋅ω⋅t)+...]
2
π
3
8h
1
⋅[sin(ω⋅t)− 2⋅sin(3⋅ω⋅t)+...]
2
π
3
Rechtecksfunktion
4
1
1
f (t)= π [sin(ω t)+ sin(3 ωt )+ sin(5 ω t)+...]
3
5
Formelsammlung.PhysMath.v24
13
Sägezahnpuls:
2h
1
1
f (t)=− π [sin (ω t)− sin( 2 ω t)+ sin (3 ω t)+...]
2
3
Sinuspuls:
4h 1 1
1
1
f (t)= π [ − cos (2 ω t)− sin (4 ωt )− sin(6 ω t )+...]
2 3
15
35
Federpendel
T =2 π
√
m
D
Fadenpendel
T =2 π
√
l
g
Akustik
Schallintensität
J=
P
A
Schwingkreis
Formelsammlung.PhysMath.v24
14
T =2 π⋅√ L⋅C
Pegel
L=10 log
J
J0
Formelsammlung.PhysMath.v24
15
Elektrizität
Coulombkraft
Q⋅q
F =k⋅ 2
r
I=
k =9⋅109 N
Q
t
m2
C2
Q:
I:
t:
Ladung
Stromstärke
Zeit
[Q ] = C = Coulomb
[I] = A = Ampere
1 C = As
Charles Augustin de Coulomb (* 14. Juni 1736 in
Angoulême; † 23. August 1806 in Paris) war ein
französischer Physiker und begründete die Elektrostatik
sowie die Magnetostatik.
André-Marie Ampère (* 20. Januar 1775 in Lyon,
Frankreich; † 10. Juni 1836 in Marseille) war ein
französischer Physiker und Mathematiker. Nach ihm ist die
internationale Einheit der Stromstärke Ampere benannt.
W
U=
Q
W:
U:
P:
W
P= =U⋅I
t
Ampere
Coulomb
Arbeit
Spannung
Leistung
[W] = 1 J = 1 Joule
[P] = 1 W = 1 Watt
[U] = 1 V = 1 Volt
AV = 1 W, Ws = 1 J
Alessandro Giuseppe Antonio Anastasio Graf von Volta (* 18. Februar 1745 in
Como, Italien; † 5. März 1827 in Camnago bei Como) war ein italienischer
Physiker. Er erfand die Batterie und gilt als einer der Begründer des Zeitalters
der Elektrizität.
R=
U
I
Formelsammlung.PhysMath.v24
R:
Widerstand
16
[R] = 1 W = 1 Ohm
Georg Simon Ohm (* 16. März
1789 in Erlangen; † 6. Juli 1854
in München) war ein deutscher
Physiker.
Serieschaltung:
Parallelschaltung
R= R1+R2+.....+Rn
1 1
1
1
= + +.....+
R R1 R2
Rn
R=
Spezifischer elektrischer Widerstand
R=ρ⋅
ℓ
A
Temperaturabhängigkeit
R(ϑ)=R 20⋅(1+α⋅Δ ϑ), Δ ϑ 20 =ϑ−20° C
Formelsammlung.PhysMath.v24
17
R1⋅R 2
R1+ R 2
Magnetismus
μ 0=4⋅π⋅10 7
Δ B=
F =I⋅l⋅B
F =q⋅v⋅B
μ0 I Δ L
⋅
4 π r2
U =v⋅B⋅l
N
A2
Lorentzkraft auf ein positiv
geladenes Teilchen der
Geschwindigkeit v (links) bzw. das
vom Strom I durchflossene
Leiterstück der Länge l (rechts) im
dazu senkrecht verlaufenden
Magnetfeld der Flussdichte B.
22.5
Halbleiter
Formelsammlung.PhysMath.v24
18
Spezifischer Widerstand ausgewählter Materialien bei 20 °
Material
Aluminium
Spez. Widerstand in Ω ·
mm2/m
2,65 ⋅ 10
−2
Lin. Widerstands3,9 ∙ 10−3
Temperaturkoeffizient in
1/°C
Chromnickel Kupfer
1,1
1,678 ⋅ 10
1,4 ∙ 10−4
3,9 ∙ 10−3
−2
Optik
Brechungsgesetz
Spezialfall: Medium und Vakuum
n=
sin α
sinβ
n=
Formelsammlung.PhysMath.v24
Allgemein
c
sin(δ 1) c 1 n2
= =
sin (δ 2) c 2 n1
c Medium
19
Wolfram
Silber
5,28 ⋅ 10
1,587 ⋅ 10−2
−2
4,1 ∙ 10−3
3,8 ∙ 10−3
Brechzahlen einiger Stoffe gegen Luft für die wichtigsten Fraunhoferschen Linien
Stoff
n_A
n_B
n_C
n_D
n_E
n_F
n_G
n_H
760,82
686,72
656,27
589
527,04
486,13
430,79
396,85
dunkelrot rot
rot
gelb
grün
blaugrün blau
Violett
Wasser
1,33
1,33
1,33
1,33
1,34
1,34
1,34
1,34
Terpentinöl
1,46
1,47
1,47
1,47
1,48
1,48
1,49
1,49
Benzol
1,49
1,49
1,5
1,5
1,51
1,51
1,52
1,53
Kohlenstoffd 1,61
isulfid
1,61
1,62
1,63
1,64
1,65
1,68
1,7
Flussspat
1,43
1,43
1,43
1,44
1,44
1,44
1,44
Borkronglas 1,5
BK1
1,51
1,51
1,51
1,51
1,52
1,52
1,52
Schwerkron- 1,6
glas SK2
1,61
1,61
1,61
1,61
1,62
1,62
1,63
Flintglas F3
1,6
1,61
1,61
1,61
1,62
1,62
1,64
1,65
Kalkspat
1,65
1,65
1,65
1,66
1,66
1,67
1,68
1,68
1,43
Bergmann/Schaefer: Optik. de Gruyter, (9)1993.
Willebrord van Roijen Snell
Willebrord van Roijen Snell (auch Snel van Royen oder Snellius; * 13. Juni
1580 in Leiden, (Niederlande); † 30. Oktober 1626 ebenda), war ein
niederländischer Astronom und Mathematiker. Er ist bekannt für die
Entwicklung des optischen Brechungsgesetzes, nach ihm als snelliussches
Brechungsgesetz bezeichnet. Er gebrauchte den Namen Snellius für
wissenschaftliche Veröffentlichungen.
Abbildungsgesetze
1 1 1
= +
f g b
Linse
Formelsammlung.PhysMath.v24
B b
=
G g
f:
g:
b:
Brennweite
Gegenstandsweite
Bildweite
Hohlspiegel
20
Linse
f≈
r
, r : Krümmungsradius
n−1
Hohlspiegel
r
f ≈ , r : Krümmungsradius
2
Linsensysteme
Linsensysteme, dünne Linsen, kleiner Abstand
1
1
1
= +
f tot f 1 f 2
Lupe
Uhrmacher
1 1 1
= +
f A b s0
1
1 1 1
+ = +
fA fL b s
Bsp:
fL = 5 cm, s0 = 25 cm
f ⋅s
s
s
1 1 1
= − → s= L 0 → Γ= 0 =1+ 0
f L s s0
f L +s 0
s
fL
6x
Briefmarkensammler
Γ=
Bsp:
s0
fL
fL = 5 cm, s0 = 25 cm
Formelsammlung.PhysMath.v24
5x
21
Brille
1 1 1
= +
fA b s
1
1 1 1
+ = +
f A f L b s0
1 1 1
1
= − → D L =4 dpt−
f L s0 s
s
Bsp: von 75 cm auf 25 cm korrigieren
75⋅25
f L=
=37.5 → D=2.66 dpt
75−25
von 75 cm auf unendlich
1 1 1
= − → f L =−75 cm → D L =−1.33 dpt
fL ∞ s
MikroskopProjektor
Fernrohr
Formelsammlung.PhysMath.v24
22
f L=
s 0⋅s
s−s 0
Kepler
s= f obj + f ok
Galilei
s= f obj − f ok
Γ=
f obj
f ok
Mikroskop
Γ=
T 0 s0
⋅
f obj f ok
s0: deutliche Sehweite
T0: Tubuslänge, Abstand der inneren Brennpunkte
Formelsammlung.PhysMath.v24
23
Wellenoptik
Formelsammlung.PhysMath.v24
24