Versuch 4 Ortskurven

Praktikum EE2
Grundlagen der Elektrotechnik
Fachbereich Elektrotechnik
Ortskurven
Name:
Versuch 4
Seite 1
Testat :
Einführung
1. Definitionen und Begriffe
1.1 Ortskurven für den Strom I und für den Scheinleistung S
Aus den Ortskurven für die Impedanz Z(f) (=komplexer Widerstand,
Scheinwiderstand) oder für die Admittanz Y(f) (=komplexer Leitwert,
Scheinleitwert) lassen sich sehr einfach die Ortskurven für den Strom I(f) und
für die Scheinleistung S(f) ermitteln.
U
2
2
I = = U ⋅Y
S = I ⋅ Z = U ⋅Y ∗
Z
Wird eine Schaltung an einer Spannung konstanter Amplitude, aber
veränderlicher Frequenz betrieben, kann die Spannung bei jeder Frequenz in
die reelle Achse gelegt werden.
Dann gilt I = U ⋅ Y d.h. die Ortskurven für den Leitwert Y(f) und für den
Strom I(f) unterscheiden sich nur durch den Maßstab der Achsen.
2
Ebenso gilt S = U ⋅ Y ∗ d.h. die Ortskurve für die Leistung S(f) entspricht der
Ortskurve für den Leitwert Y(f), gespiegelt an der reellen Achse (umgeklappt um
die reelle Achse); allerdings müssen auch hier die Maßstäbe der Achsen
geändert werden.
1.2 Frequenzgang, Bode-Diagramm
Der Frequenzgang ist die Abhängigkeit einer sinusförmigen Größe (bzw. einer
komplexen Leistung) von der Frequenz. Die Frequenzabhängigkeit der
Amplitude ist der Amplitudengang oder Betragsgang und die
Frequenzabhängigkeit des Phasenwinkels ist der Phasengang. Nach einem
Vorschlag von Hendrik W. Bode werden in dem nach ihm benannten DodeDiagramm die Amplitude und die Frequenz logarithmisch dargestelt. Der
Phasenwinkel kann nicht logarithmisch dargestellt werden, da er auch Null
werden kann.
1.2.1 Übertragungsfaktor, Übertragungsfunktion A(ω) bzw. A(f)
Der Übertragungsfaktor A(ω) (auch Übertragungsfunktion genannt) ist bei
einem Vierpol das Verhältnis der Ausgangsspannung Ua zur
Eingangsspannung Ue.
U (ω )
A(ω ) = a
U e (ω )
1.3 Resonanzfrequenz
Bei der Resonanzfrequenz ist der Imaginärteil des Leitwertes bzw. des
Widerstandes Im {Y } = 0 bzw. Im {Z } = 0 , d.h. der Widerstand bzw. der
Leitwert ist reell (rein ohmsches Verhalten), Strom und Spannung sind in
Phase, die Schaltung nimmt nur Wirkleistung auf.
Praktikum EE2
Versuch 4
Grundlagen der Elektrotechnik
Fachbereich Elektrotechnik
Ortskurven
Seite 2
1.3.1 Lissajous- Figuren
Mit Hilfe der Lissajous-Figuren kann mit einem Oszilloskop sehr leicht die
Frequenz ermittelt werden, bei die Phasenverschiebung zwischen Strom und
Spannung ϕ=0 ist.
u x ( t ) = uˆ ⋅ sin ( t )
u y ( t ) = uˆ ⋅ sin ( t + ϕ )
Es können auch Phasenwinkel zwischen 00 und 900 ermittelt werden.
1.4 Maximum oder Minimum für Strom, Leistung
Das Minimum bzw. Maximum der Leistung bzw. des Stromes ist bei den
Frequenzen, bei denen der Leitwert Y(f) minimal bzw. maximal wird. Ermittelt
wird der Wert mit Hilfe des Zirkels aus der Ortskurve.
1.5 Reale Bauelemente
Wenn durch eine Spule ein Strom fließt und wenn an einem Kondensator eine
Spannung anliegt, treten Verluste auf. Diese Verluste werden durch einen
Widerstand in Reihe zur Induktivität und parallel zur Kapazität berücksichtigt.
tan ϕ z =
X ω ⋅L
=
= ω ⋅τ
Rr
Rr
Rr
ω⋅L
tan δ = Verlustfaktor
δ = Verlustwinkel
tan ϕ y =
B
= ω ⋅ C ⋅ R p = ω ⋅τ
Gp
tan δ =
Gp
tan δ =
ω ⋅C
=
1
ω ⋅ Rp ⋅ C
Bei Kondensatoren ist der Verlustfaktor so klein, daß in vielen Fällen der
Parallelwiderstand als unendlich groß angenommen werden kann.
Praktikum EE2
Grundlagen der Elektrotechnik
Fachbereich Elektrotechnik
Ortskurven
Versuch 4
Seite 3
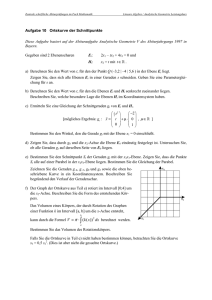
2. Parallelschwingkreis mit realen Bauelementen
Schaltung:
R = 40Ω ; L = 30mH ; C = 4μF
Versuchsdurchführung:
2.1 Werte für Ortskurve
Ermitteln Sie die Ortskurven Z(f) und Y(f). Messen Sie dazu Spannung, Strom
und Leistung, rechnen Sie cos(ϕ)=P/U.I, kontrollieren Sie die Werte mit einem
Oszilloskop. Beachten Sie, dass der Leistungsfaktor cosϕ immer positiv ist
(sowohl bei kapazitivem als auch bei induktivem Verhalten der Schaltung)
Hinweis 1: Tragen Sie während der Messungen die Werte in eine Skizze für die
Ortskurve ein. Nur so können Sie sinnvolle Parameterwerte wählen und feststellen,
an welchen Stellen noch Werte fehlen.
Hinweis 2: Beginnen Sie sinnvollerweise mit einer Frequenz, bei der
entweder
ϕ=0 (Resonanz)
oder
Strom I minimal oder maximal
oder
ϕ = +450 oder ϕ = -450
oder
ω.L = R
2.1.1 Werte bei Resonanz
Ermitteln Sie bei Resonanz die Frequenz sowie U, I, S, Y, Z
2.1.2 Maximum bzw. Minimum
Ermitteln Sie bei dem Maximum bzw. Minimum der Leistung die Frequenz
sowie U, I, S, Y, Z
Praktikum EE2
Grundlagen der Elektrotechnik
Fachbereich Elektrotechnik
Ortskurven
Versuch 4
Seite 3
2.2 Darstellungen
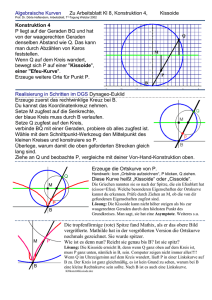
2.2.1 Ortskurve für Y(f)
Zeichnen Sie die Ortskurve
2.2.2 inverse Ortskurve Z(f)
Konstruieren Sie mit den interpolierten Werten aus der Ortskurve Y(f) die
inverse Ortskurve Z(f) und vergleichen Sie die konstruierte Ortskurve mit den
Meßwerten für Z.
Hinweis: Wegen der unvermeidlichen Messfehler für Spannung, Strom und Leistung
ergeben sich insbesondere bei der Division noch größere Fehler.
Tragen Sie deshalb die gemessenen Werte U(f), I(f) und P(f) in ein Diagramm ein, legen
Sie eine Ausgleichskurve durch die Messwerte und lesen Sie die Werte zum Berechnen
und Zeichnen der Ortskurve aus dieser neuen Kurve ab.
Ebenso entnehmen Sie die Werte für die Inversion der Ortskurve aus der gezeichneten
Ortskurve Z(f) und benutzen Sie nicht die ursprünglich gemessenen Werte.
2.2.3 Berechnungen
1. Berechnen Sie die Resonanzfrequenzen fres für unterschiedliche
Dämpfungswiderstände Rd und zeichnen Sie fres=f(Rd).
2. Berechnen den Dämpfungswiderstand, bei dem keine Schwingung mehr
auftritt und zeigen Sie, daß zwar ein Minimum des Stromes auftritt, aber
keine Resonanz (d.h. kein Wechsel vom induktiven zum kapazitiven
Verhalten).
Praktikum EE2
Grundlagen der Elektrotechnik
Fachbereich Elektrotechnik
Ortskurven
Versuch 4
Seite 4
3. Reihenschwingkreis mit realen Bauelementen
Schaltung:
R=50Ω ; L=30mH ; C=4μF
Versuchsdurchführung:
3.1 Werte für Ortskurve
Ermitteln Sie die Ortskurven Z(f) und Y(f). Messen Sie dazu Spannung, Strom
und Leistung, rechnen Sie cos(ϕ)=P/U.I, kontrollieren Sie die Werte mit einem
Oszilloskop. Beachten Sie, dass der Leistungsfaktor cosϕ immer positiv ist
(sowohl bei kapazitivem als auch bei induktivem Verhalten der Schaltung)
Hinweis 1: Tragen Sie während der Messungen die Werte in eine Skizze für die
Ortskurve ein. Nur so können Sie sinnvolle Parameterwerte wählen und feststellen,
an welchen Stellen noch Werte fehlen.
Hinweis 2: Beginnen Sie sinnvollerweise mit einer Frequenz, bei der
entweder
ϕ=0 (Resonanz)
oder
Strom I minimal oder maximal
oder
ϕ = +450 oder ϕ = -450
3.1.1 Werte bei Resonanz
Ermitteln Sie bei Resonanz die Frequenz sowie U, I, S, Y, Z
3.2 Darstellungen
3.2.1 Ortskurve für Y(f).
Zeichnen Sie die Ortskurve