Zentralprojektion

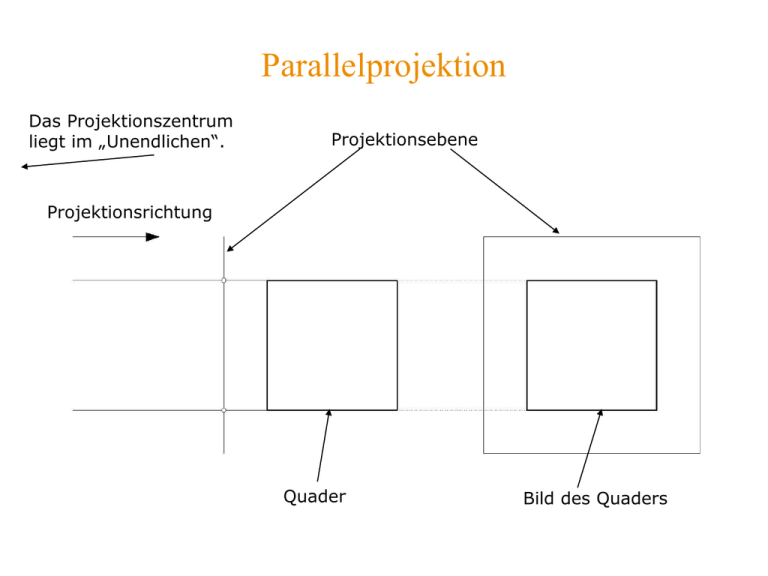
Parallelprojektion
Das Projektionszentrum
liegt im „Unendlichen“.
Projektionsebene
Projektionsrichtung
Quader
Bild des Quaders
Zentralprojektion – Auge und Kamera
Sowohl das Sehen mit dem Auge als auch das Fotografieren sind
praktisch Zentralprojektionen
Projektionszentrum – Linse
Bildebene - Netzhaut
Projektionszentrum – Objektiv
Bildebene - Filmebene
Projektionen
Zentralprojektion – zeichnerische Perspektive
Projektionsebene
Projektionszentrum
Quader
Bild des Quaders
Invarianten bei einer Projektion
Zentralprojektion zwischen Ebenen allgemeiner Lage:
Inzidenz, Doppelverhältnis
 perspektive Kollineation
Parallelprojektion zwischen Ebenen allgemeiner Lage:
Inzidenz, Parallelität, Teilverhältnis
 perspektive Affinität
Zentralprojektion zwischen parallelen Ebenen:
Inzidenz, Parallelität, Teilverhältnis, Winkel
 Ähnlichkeit
Parallelprojektion zwischen parallelen Ebenen:
Inzidenz, Parallelität, Teilverhältnis, Winkel, Flächeninhalt
 Kongruenz
Zentralprojektion - Bezeichnungen
Hauptpunkt

Bildebene
Horizont
H
Projektionszentrum
h
h
X‘‘
d
e
X
Z
H
Xc
Xc
e
g
H‘
d
H‘
X‘
Z‘
Grundgerade
Z0
=1
Standebene
Bildpunkt / Durchstoßpunkt Xc (zu X)
ist der Spurpunkt des Sehstrahles ZX in der Bildebene:
Xc := ZX  
g
Abstand Objekt – Bildebene veränderlich
Abstand Objekt - Projektionszentrum gleich
Abstand Objekt - Projektionszentrum veränderlich
Abstand Objekt – Bildebene gleich
Vergleich Parallelprojektion - Zentralprojektion
Bei einer Parallelprojektion hängt das Bild
von der Projektionsrichtung bezogen auf
das darzustellende Objekt ab.
Bei einer Zentralprojektion hat der Abstand
des Projektionszentrums (Betrachters) zum
Objekt einen sehr großen Einfluss auf das
Bild.
Parallelprojektion
Betrachter nah
am Objekt
Betrachter weiter vom
Objekt entfernt
Zentralprojektion
Verfälschung da
Projektionszentrum
innerhalb des Objekts
Fluchtpunkte
Die perspektivischen Bilder von im Raum parallelen Geraden
schneiden sich in einem Punkt, dem Fluchtpunkt.
Fluchtpunkte von Höhen- und Tiefengeraden
Der Fluchtpunkt einer Höhengerade (zur Standebene parallele Gerade) liegt
auf dem Horizont. Die Bilder von Tiefengeraden (zur Bildebene senkrechte
Gerade) schneiden sich im Hauptpunkt.
H
Horizont
Albrecht Dürer (1471 – 1525)
„Der Zeichner der Laute“
Durchstoßverfahren
2
Xc‘‘
Xc

H
h
d
X‘‘
H‘‘
X
Z
Xc‘‘
h‘‘
Z‘‘
H‘‘
X‘‘
Z‘‘
x12
Xc‘
g
H‘
Xc‘
X‘
Z‘
H‘
X‘
1
g
Z‘
Abbildung eines Punktes
Xc‘‘
X‘‘
H‘‘
h‘‘
y-Achse
Z‘‘
Xc
h
H
yc
yc
xc
g
x12
H‘ = O
Konstruktionsvorschrift
geg.:
X, Z in Grund- und Aufriss und Grundriss von  ( 1 = )  g und
g (=   ) und H in Zeichenebene
Xc := zentr(X; , Z)
 Ablauf
H’ := (Z’  g)  g
Xc’ := Z’X’  g
Xc’’ := ord(Xc’)  Z’’X’’
xc =
c
Xc‘
xc
x-Achse
X‘
H‘
H'X '
g
Z‘
yc =
x12 X c ''
Xc := (xc, yc) bezüglich KS(H’; x, y) / KS …
Koordinatensystem mit g als x-Achse und H’H als y-Achse
Fluchtpunkt einer Geraden
Fa
h

H
A
Z
a
a*
=1
a* : (Z a)
X
Der Fluchtpunkt Fa der
Geraden a ist der
Spurpunkt der zu a
parallelen Geraden a*
durch Z:
Fa  (Z a)  
Xc
ac
Daher gilt auch:
a  (A Fa Z)
Das heißt:
Die Lage einer Geraden a
ist durch ihren Spurpunkt A
und ihren Fluchtpunkt Fa
umkehrbar eindeutig
bestimmt.
a b  F
a
a    F (i.d.R.  H )  h
1
=
1
a
a     2   Fa  H  h
 Fb  Fc
Eigenschaften einer Zentralprojektion
(Abbildung von Geraden)
Parallele Geraden    haben denselben Fluchtpunkt:
a b  F
a
 Fb
Der Fluchtpunkt von Höhengeraden liegt auf dem Horizont:
a    F  h
1
a
Der Fluchtpunkt der Tiefengeraden ist der Hauptpunkt H:
a    Fa  H
Für zu  parallele Geraden gilt:
a a 
c
d.h.
A  Fa
ist uneigentlich. (Spurpunkt
A : a  
)
Abbildung einer Geraden (mit Durchstoßverfahren)
a‘‘
ac
Z‘‘
A‘‘
H
Ac
Fa‘‘
Fa
qA=yA
x12
pA=xA
H‘ = O
Fa‘
H‘
A‘
g=‘
h
Z‘
a‘
g
Zentralriss eines Quaders – Wahl des Augpunkts
b

Der Blickwinkel  wird durch die beiden
äußeren Projektionsstrahlen bestimmt.
Die Ausdehnung b ist der Abstand
zwischen den beiden Schnittpunkten
dieser Strahlen mit .
Faustregel:
  40° (besser   40°)
1,5 · b < d < 3 · b
Der Hauptstrahl soll etwa den Schwerpunkt des Objekts berühren bzw.
Winkelhalbierende des Blickwinkels sein.
Eigenschaften einer Zentralprojektion
(Abbildung von Ebenen)
Parallele Ebenen (aber nicht
dieselbe Fluchtgerade:
 D  f Σ  f D
   ) haben
Die Fluchtgerade von Höhenebenen
ist der Horizont h:
   f
h

Die Fluchtgerade von Tiefenebenen
verläuft durch den Hauptpunkt H:
    H  f 
Der Fluchtpunkt einer parallelen
Geraden liegt auf der
Fluchtgeraden der Ebene:
a   F
a
 f
Analog zur Abbildung einer Geraden werden Ebenen  durch
ihre Spur(-gerade)
s     und ihre
Fluchtgerade (Fluchtspur)
c
f   su  ( Z  )  
dargestellt, wobei
f  der Zentralriss suc der uneigentli chen
Geraden su von  ist; es gilt : suc s
Die Spurgerade s und die Fluchtgera de f   suc einer
Ebene  bestimmen die Ebene  umkehrbar eindeutig :
  ( s , suc ). Es ist   s suc Z .
Wahre Strecke PQ einer Frontgeraden, senkrecht
Wahre Länge einer Strecke – Frontgerade, nicht senkrecht
4.
P0
Pc
6.
l
h
1.
F
5.
Qc
Q0
3.
Sc
a0
g
S0
2.
 Ablauf:
1. F  h beliebig
2. S0 := FSc  g
3. a0 := S0 || PcQc
4. P0 := FPc  a0
5. Q0 := FQc  a0
6. l := P0Q0
Wahre Länge einer Strecke (Gerade a in der Grundebene) – Messpunkt Ma

Q
a
‘=g
Ma
H
Fa
Ma´
ac
Qc
a
q
P
H´
A
Q
Fa´
p
P0
Q0
P
Pc
Z
A
P0
Q0
a

Der gesuchte Punkt P0 ist der Schnittpunkt der
Geraden MaPc mit der Grundgeraden g.
Z´
Die Gerade a=PQ c Γ wird
um A so gedreht, daß sie
in П liegt. Dann ist die
wahre Länge P0 Q0 dort
abzulesen:
Die Drehsehnen p=PP0
und q=QQ0 sind parallel.
Ihr gemeinsamer
Fluchtpunkt Fp,q= Ma liegt
auf dem Horizont und wird
Messpunkt oder
Maßpunkt von a genannt.
Wahre Länge einer Strecke – Gerade a der Grundebene
Ma
Fa
H
h
ac
Qc
d
Pc
g
A
Z0
P0
Q0
Wahre Länge einer Strecke – Allgemeine Lage
Fa
ac
H
Z0=Ma
h
Q0
Qc
d
Pc
P0
k
A
a0
K
Bestimmung der Standardanordnung - Hauptpunkt
Variante 1:
Bei einem vollständigen Foto liegt der Hauptpunkt in der Mitte des Fotos
(Schnittpunkt der Diagonalen).
Variante 2:
Werden zur Bildebene parallele ebene Figuren ähnlich abgebildet, d.h. ist
zum Beispiel das Bild eines Rechtecks wieder ein Rechteck, so sind die Bilder
der zu dieser Figur senkrechten Geraden Tiefengeraden und schneiden sich
perspektivisch im Hauptpunkt.
Hauptpunkt
Bestimmung der Standardanordnung - Horizont
Variante 1:
Der Horizont h ist das Lot zum Bild einer vertikalen Geraden, durch einen
Fluchtpunkt F1 , F2 einer horizontalen Geraden.
Variante 2:
Der Horizont h ist durch die Fluchtpunkte von zwei nicht zueinander
parallelen Höhengeraden bestimmt.
F1
F2
Bestimmung der Standardanordnung - Distanz
Sind der Hauptpunkt und zwei Fluchtpunkte von zueinander senkrechten
Höhengeraden bekannt, so lässt sich die Distanz mit Hilfe des ThalesKreises über die beiden Fluchtpunkte bestimmen.
F´2
Thales-Kreis
(2r= F1F2 )
Distanz d
F´1
Rekonstruktion - Projektionszentrum
F1
H
F2
h
geg.: Zentralriss, h, H, g,
notwendige Fluchtpunkte
und: ’ (= g) || g in Zeichenebene
geeignet wählen
Z’ konstruieren
F1‘
H‘
F2‘
‘
Thales-Kreis k
 Ablauf (geg. F1, F2 geeignet)
F1’ := (F1  g)  ’
F2’ := (F2  g)  ’
k := thkr(F1’, F2’)
Z’ := k  (H  g)
Z‘
Rekonstruktion – Gerade in der Grundebene
H
Fa
Sac
Fa‘
a‘
g
ac
H‘
Sa ‘
a’ := grundr(a: a  )
 Ablauf:
Fa’ := (Fa  g)  ’
Sac := ac  g
Sa’ := (Sac  g)  ’
a’ := Sa’ || Fa’Z’
Z‘
‘
Rekonstruktion – Punkt in der Grundebene
H
Pc
g
ac
P‘
‘
Pg
a‘
P’ := grundr(P: P  )
 Ablauf:
a beliebig mit P  a und a  
a’ := grundr(a: a  )
Pg := (Pc  g)  ’
P’ := PgZ’  a’
Z‘
Rekonstruktion – Grundriss eines Quaders
H
g
‘
Z‘
Rekonstruktion – Grund- und Aufriss
Konstruktion
der wahren
Länge einer
zur Bildebene
parallelen
Strecke.
l
H
l
g
‘
l
x12
Z‘
Wenn eine
Strecke in der
Bildebene
liegt, wird sie
kongruent,
d.h. in wahrer
Länge,
abgebildet.